
- •Содержание
- •1. Понятие числового ряда и его суммы
- •2. Свойства сходящихся рядов
- •3. Достаточные признаки сходимости рядов с неотрицательными членами
- •4. Знакопеременные ряды
- •5. Знакочередующиеся ряды
- •5.Функциональные ряды.
- •6. Степенные ряды
- •7. Разложение функций в степенные ряды.
- •8. Приложения степенных рядов.
7. Разложение функций в степенные ряды.
Функция разлагается в степенной ряд или в ряд , если:
1) этот степенной ряд сходится; 2) его сумма на интервале сходимости равна .
Известно, что функцию можно разложить в ряд Тейлора. Однако, чисто формальное разложение в ряд Тейлора может привести к неверному результату, т.к.
1) ряд может сходиться к только в некоторой области; 2) ряд может сходиться, но не к ; 3) ряд может расходиться.
Рассмотрим условия разложения функции в ряд Тейлора.
Теорема 7.1. Для того чтобы ряд Тейлора сходился к функции необходимо и достаточно, чтобы остаточный член ряда стремился к 0 при .
Теорема
7.2. Если
производные любого порядка функции
ограничены одной и той же постоянной,
т.е.
![]() ,
,
![]() ,
,
![]() ,
то ряд Тейлора сходится в
,
то ряд Тейлора сходится в
![]() к
.
к
.
Теорема 7.3. Разложение функции в ряд Тейлора единственно.
Приведем разложение основных элементарных функций в степенные ряды.
1)
![]() ,
,
2)
![]() ,
,
3)
![]() ,
,
4)
![]() ,
,
5)
![]() ,
,
6)
![]() ,
,
![]()
7)
![]() ,
,
![]()
8)
![]() ,
,
![]()
9)
![]() ,
,
Пример
23. Разложите
функцию
![]() в ряд Тейлора по степеням
.
в ряд Тейлора по степеням
.
Решение.
Так как
,
то
![]() .
Так как разложение для
.
Так как разложение для
![]() действительно при
,
то и функция
разлагается
в ряд Тейлора при
.
действительно при
,
то и функция
разлагается
в ряд Тейлора при
.
Пример 24.
Разложите функцию
![]() в ряд Тейлора по степеням
.
в ряд Тейлора по степеням
.
Решение.
Представим дробь
![]() в виде суммы простейших дробей:
в виде суммы простейших дробей:
![]()
и разложим каждую простейшую дробь в правой части равенства по формуле для суммы бесконечно убывающей геометрической прогрессии:
![]() ,
где
.
,
где
.
 .
.
Это разложение
имеет место лишь для
,
удовлетворяющих неравенству
![]() или
или
![]() .
.
Так как
для
,
![]() для
,
то разложение функции
для
,
то разложение функции
![]()
![]() верно при
(как пересечение областей сходимости).
верно при
(как пересечение областей сходимости).
Пример
25. Разложите
функцию
![]() в ряд Тейлора по степеням
.
в ряд Тейлора по степеням
.
Решение.
Разложим аргумент логарифма на множители:
![]() .
Тогда
.
Тогда
![]() .
И, применяя формулу
,
где
,
запишем:
.
И, применяя формулу
,
где
,
запишем:
![]() ,
,
это представление
верно при
![]() или
или
![]() .
.
![]() ,
,
это равенство
имеет место при
![]() или
или
![]() .
.
Объединяя полученные
результаты, получаем разложение данной
функции в ряд Тейлора по степеням
![]() :
:
![]() ,
,
причём это разложение
справедливо при
![]()
8. Приложения степенных рядов.
Рассмотрим следующие приложения степенных рядов:
1) Приближенное
вычисление значений функции. Функцию
разлагают в степенной ряд, оставляют
первые n
членов.
Погрешность равна остатку ряда
![]() .
Для оценки погрешности применяют приёмы:
.
Для оценки погрешности применяют приёмы:
а) если ряд
![]() знакоположительный, его сравнивают с
геометрической прогрессией;
знакоположительный, его сравнивают с
геометрической прогрессией;
б) если ряд
![]() знакочередующийся, применяют признак
Лейбница, т.е. используют свойство
знакочередующийся, применяют признак
Лейбница, т.е. используют свойство
![]() .
.
Пример 26. Оценить погрешность приближённого равенства
![]()
Решение.
![]()
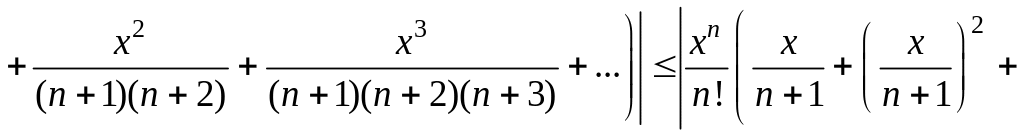

Если
![]() ,
то, применяя к выражению в скобках
формулу для суммы бесконечно убывающей
геометрической прогрессии, получаем
,
то, применяя к выражению в скобках
формулу для суммы бесконечно убывающей
геометрической прогрессии, получаем
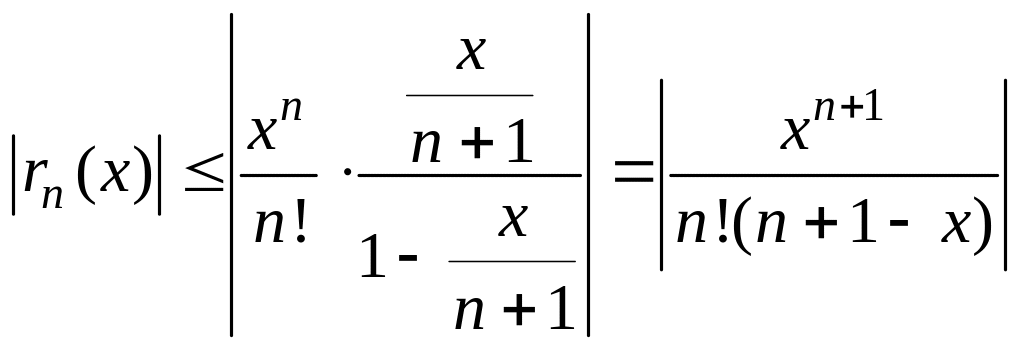 .
.
Таким образом,
![]() .
.
Пример
27. Вычислить
![]() точностью до 10-4.
точностью до 10-4.
Решение.
Так как
![]() ,
то, применяя формулу
,
то, применяя формулу
![]()
![]() при
при
![]() ,
запишем
,
запишем
![]()
В правой части
этого равенства числовой знакочередующийся
ряд. По признаку Лейбница сумма такого
ряда не превосходит первого отброшенного
члена. Заметим, что
![]() ,
поэтому для вычисления суммы
знакочередующегося ряда достаточно
взять первые два слагаемых и считать,
что
,
поэтому для вычисления суммы
знакочередующегося ряда достаточно
взять первые два слагаемых и считать,
что
![]() .
.
2) Приближенное вычисление пределов.
Пример
28. Вычислите
приближенно предел
![]() .
.
Решение.
При
![]() получаем неопределенность вида
получаем неопределенность вида
![]() .
Но применять таблицу эквивалентных
бесконечно малых нельзя, так как в
числителе разность бесконечно малых
одного порядка. Вычислим этот предел,
разложив слагаемые в числителе в
степенные ряды.
.
Но применять таблицу эквивалентных
бесконечно малых нельзя, так как в
числителе разность бесконечно малых
одного порядка. Вычислим этот предел,
разложив слагаемые в числителе в
степенные ряды.
![]()
это разложение верно для любых действительных .
![]()
это разложение
имеет место при
,
но
![]() ,
поэтому в нашем случае можно применить
указанное представление.
,
поэтому в нашем случае можно применить
указанное представление.
С учётом вышесказанного запишем:

![]() .
.
3) Приближенное вычисление интегралов.
Пример 29.
Вычислите
интеграл
 точностью до
точностью до
![]() .
.
Решение.
Разложим
![]() в ряд Тейлора по степеням
:
в ряд Тейлора по степеням
:
Тогда
![]()
![]()
Подставим полученное разложение подынтегральной функции в исходный интеграл:
 .
.
Под знаком интеграла
степенной ряд
![]() .
Применяя обобщенный признак Даламбера,
можно доказать, что этот ряд сходится
при любом действительном
.
.
Применяя обобщенный признак Даламбера,
можно доказать, что этот ряд сходится
при любом действительном
.
Следовательно, он
сходится равномерно на отрезке
![]() .
Поэтому его можно почленно интегрировать
на этом отрезке. Проинтегрируем:
.
Поэтому его можно почленно интегрировать
на этом отрезке. Проинтегрируем:

В правой части
равенства
числовой знакочередующейся ряд, его
сумма по признаку Лейбница не превосходит
первого отброшенного члена. Так как
![]() ,
то для вычисления интеграла с указанной
точностью достаточно взять первые два
слагаемых, т.е.
,
то для вычисления интеграла с указанной
точностью достаточно взять первые два
слагаемых, т.е.
 .
.
