УДК 517.5

ББК 22.19

Составители: С.В. Бушков, Л.В. Коломиец

Рецензент: д-р техн. наук, проф. Б.А. Горлач

Приложения и приближенное вычисление определенных интегралов: метод. указания / сост. С.В. Бушков, Л.В. Коломиец. - Самара: Изд-во Самар. гос. аэрокосм. ун-та, 2009. – 48 с.

Методические указания составлены в соответствии с действующей программой по курсу высшей математики для инженерно-технических специальностей Самарского государственного аэрокосмического университета. Указания обеспечивают полную теоретическую и методическую поддержку практических занятий по темам «Приложения определенного интеграла» и «Приближенное вычисление определенных интегралов».

Методические указания могут быть рекомендованы студентам для самостоятельной работы и подготовки к экзаменам.

© Самарский государственный

аэрокосмический университет, 2009

Содержание

1. Площадь плоской фигуры в декартовых координатах…………………………

2. Площадь плоской фигуры при параметрическом

задании границ…………………………………………………………………..8

3. Площадь плоской фигуры в полярных координатах………..………….....11

1. Понятие числового ряда и его суммы

Рассмотрим числовую последовательность Составим из неё новую последовательность по правилу:

,

,

,

. . . . . . . . . . . .

,

. . . . . . . . . . .

Определение 1. Выражение называется числовым рядом, числа называются членами ряда, – общим членом, − n-ой частичной суммой ряда.

Определение 1. Числовой ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм при , т.е. . Число называется суммой числового ряда, в этом случае записывают: . Если или не существует, то ряд называется расходящимся.

Пример 1. Рассмотрим геометрическую прогрессию

Из школьного курса математики известно, что сумма её первых членов равна

Возможны следующие случаи:

1) Если , то , следовательно, , т.е. ряд расходится.

2) Если , то следовательно,

, т.е. ряд сходится.

3) Если , то , т.е. сумма нечетного числа членов ряда , а сумма четного числа членов . Получили последовательность частичных сумм которая не имеет предела. Следовательно, при ряд расходится.

Таким образом, ряд , составленный из членов геометрической прогрессии, сходится при и расходится при .

Пример 2. Найдите сумму ряда .

Решение. Разложим общий член ряда на простейшие дроби:

.

Найдём n-ую частичную сумму ряда:

Заметим, что второе слагаемое скобки с номером «к» взаимно уничтожается с первым слагаемым скобки с номером «к+1», поэтому в итоге частичная сумма ряда имеет вид: .

Найдем предел:

Ответ: сумма данного ряда равна

2. Свойства сходящихся рядов

Теорема 1. Если сходится ряд , то сходится и его остаток , и наоборот. Другими словами, на сходимость ряда не влияет отбрасывание или добавление конечного числа членов.

Теорема 2. Если ряд сходится к сумме , то ряд , где – const, сходится к сумме .

Теорема 3. Если сходятся ряды и , и их суммы соответственно равны и , то сходится и ряд , и его сумма равна (обратное неверно).

Теорема 4 (Необходимый признак сходимости ряда). Если ряд сходится, то . (2.1)

Отсюда следует, что если условие (2.1) не выполнено, то ряд расходится.

Условие (2.1) является необходимым, но не достаточным условием сходимости ряда.

Пример 3. Исследуйте на сходимость ряд .

Решение. Найдём , т.е. необходимое условие

сходимости ряда выполняется. Тем не менее, ряд расходится, т.к.

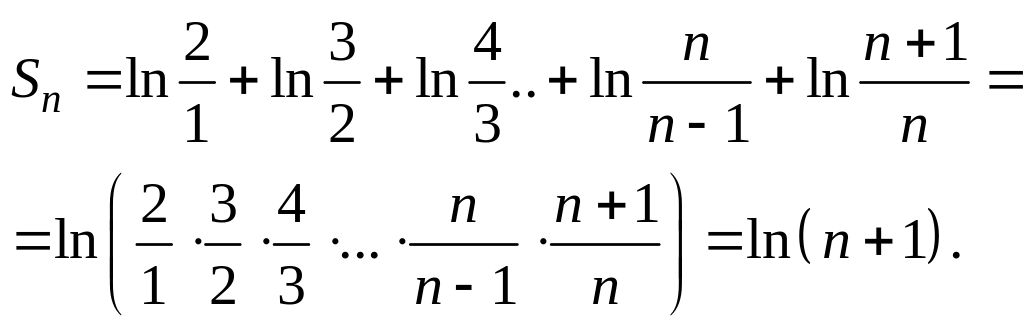
Пример 4. Исследуйте на сходимость ряд

Решение. Так как , то необходимый признак не выполняется и ряд расходится.

3. Достаточные признаки сходимости рядов с неотрицательными членами

Теорема 5. (признак сравнения). Пусть для членов рядов и имеет место неравенство

(для всех n или начиная с некоторого n). Тогда:

1) если сходится ряд , то сходится и ряд ;

Если сходится ряд с большими членами, то сходится и ряд с меньшими членами. Обратное неверно.

2) если расходится ряд , то расходится и ряд .

Если расходится ряд с меньшими членами, то расходится и ряд с большими членами. Обратное неверно.

Пример 5. Исследуйте на сходимость ряд .

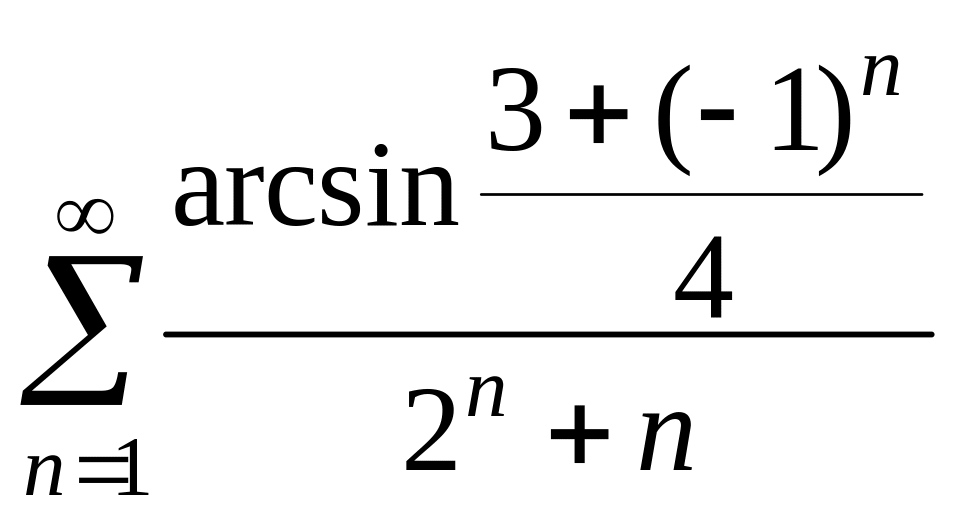Решение. Так как при четных ,

и при нечётных , то числитель общего члена ряда принимает только два значения: и . Можно записать следующую оценку: .

Больший ряд составлен из членов геометрической прогрессии, где , и следовательно сходится. Тогда по признаку сравнения сходится и ряд с меньшими членами .

Теорема 6. (предельный признак сравнения). Пусть , , и существует предел . Тогда ряды и ведут себя одинаково, т.е. сходятся или расходятся одновременно.

Теорема 7. (признак Даламбера). Пусть для ряда существует предел . Тогда:

1) если , то ряд сходится;

2) если , то ряд расходится;

3) если , то требуется дополнительное исследование по другим достаточным признакам.

Пример 6. Исследуйте на сходимость ряд .

Решение. , . Найдём

Следовательно, по признаку Даламбера данный ряд расходится.

Пример 7. Докажите справедливость равенства .

Решение. Рассмотрим ряд и применим к нему признак Даламбера. Найдём предел:

. Следовательно, по признаку Даламбера ряд сходится. Но тогда по необходимому признаку сходимости предел общего члена равен нулю: .

Теорема 8. (радикальный признак Коши). Пусть для ряда существует предел . Тогда:

1) если то ряд сходится;

2) если , то ряд расходится;

3) если , то требуется дополнительное исследование по другим достаточным признакам.

Пример 8. Исследуйте на сходимость ряд .

Решение. Найдём предел:

.

Следовательно, по радикальному признаку Коши ряд сходится.

Теорема 9. (интегральный признак Коши). Пусть члены ряда имеют вид , где – неотрицательная, монотонно убывающая функция на промежутке . Тогда ряд сходится (расходится) тогда и только тогда, когда сходится (расходится) несобственный интеграл .

Пример 9. Исследуйте на сходимость обобщенно-гармонический ряд Дирихле .

Решение. Если то общий член ряда при стремится к бесконечности и ряд расходится по необходимому признаку. При имеем расходящийся гармонический ряд. При положим . Функция непрерывна и монотонно убывает на промежутке . Известно, что несобственный интеграл сходится при и расходится при . Следовательно, по теореме 3.5 ряд Дирихле сходится при и расходится при .

Пример 10. Исследуйте на сходимость ряд .

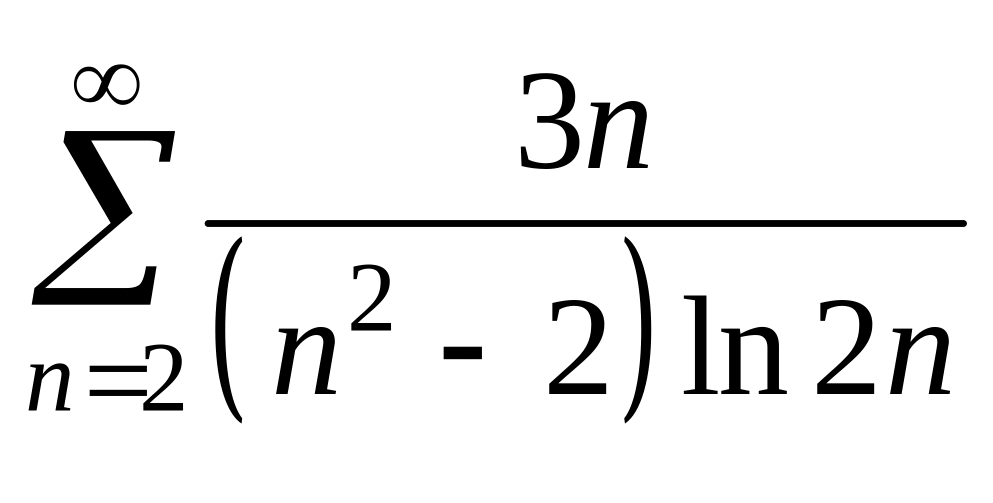Решение. Непосредственное применение интегрального признака приводит к интегралу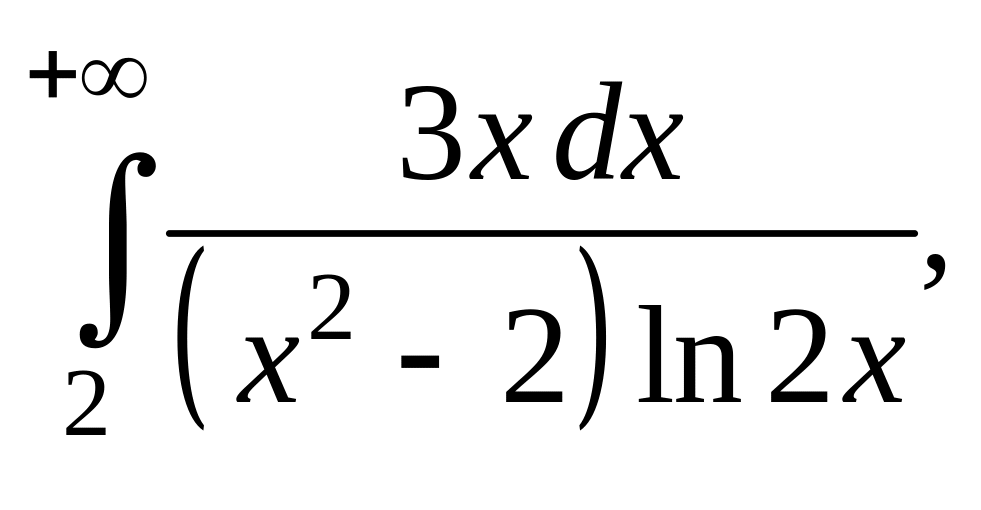 вычислить который довольно сложно. Поступим по-другому. Подберем ряд, эквивалентный данному в смысле сходимости. Рассмотрим ряд .

Применим предельный признак сравнения. Вычислим 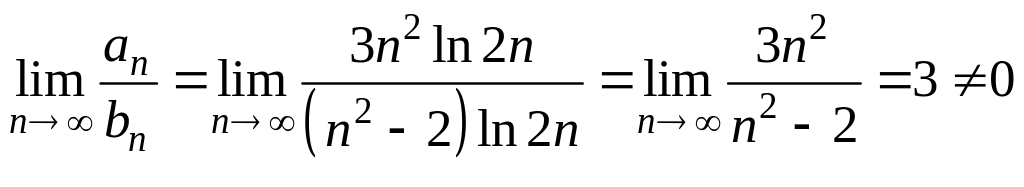. Следовательно, ряды и сходятся или расходятся одновременно по предельному признаку сравнения. Исследуем теперь ряд по интегральному признаку. Вычислим интеграл

Несобственный интеграл расходится, следовательно по интегральному признаку ряд расходится, тогда данный ряд также расходится по предельному признаку сравнения.

Рассмотрим еще один пример на применение предельного признака сравнения.

Пример 11. Исследуйте на сходимость ряд .

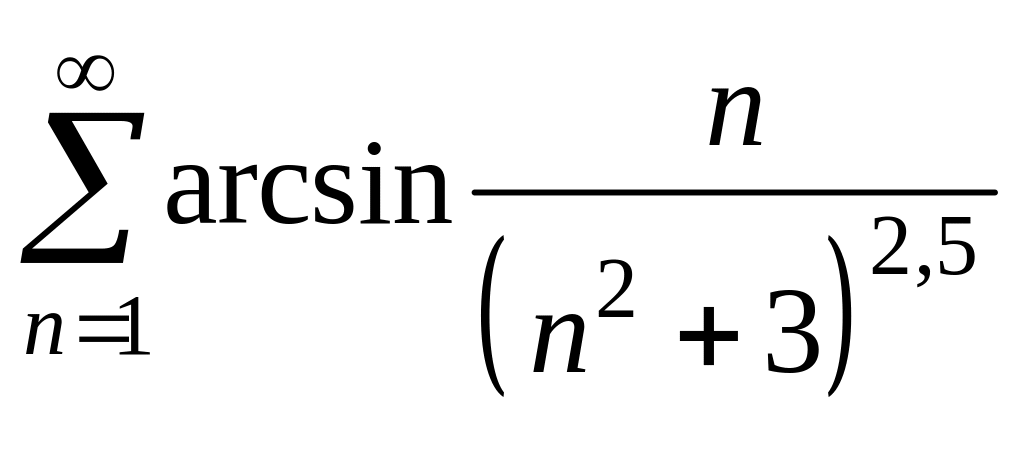Решение. Рассмотрим ряд . Это обобщенно-гармонический ряд Дирихле, он сходится, т.к. степень Применим предельный признак сравнения. Вычислим предел:

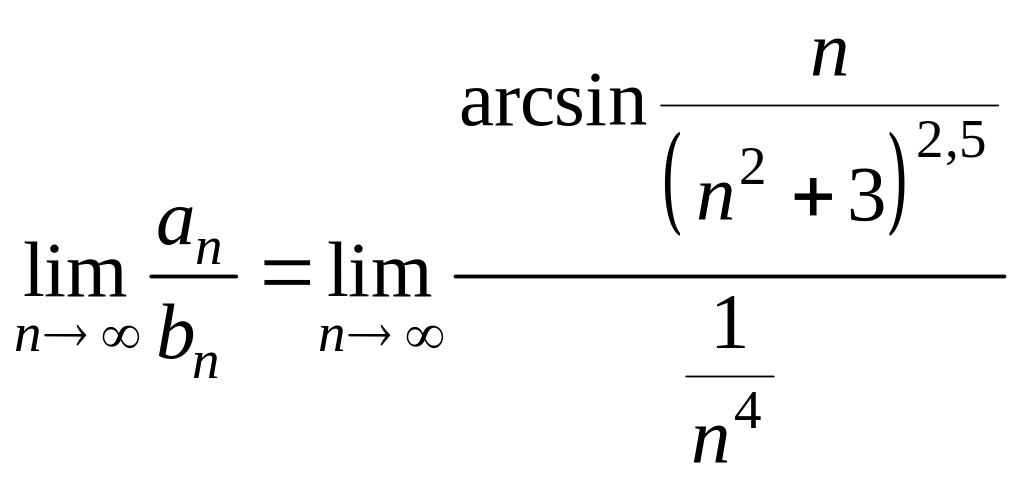. Так как при аргумент арксинуса

стремится к нулю, является бесконечно малой величиной. По таблице эквивалентных бесконечно малых можно заменить в пределе на эквивалентную бесконечно малую :

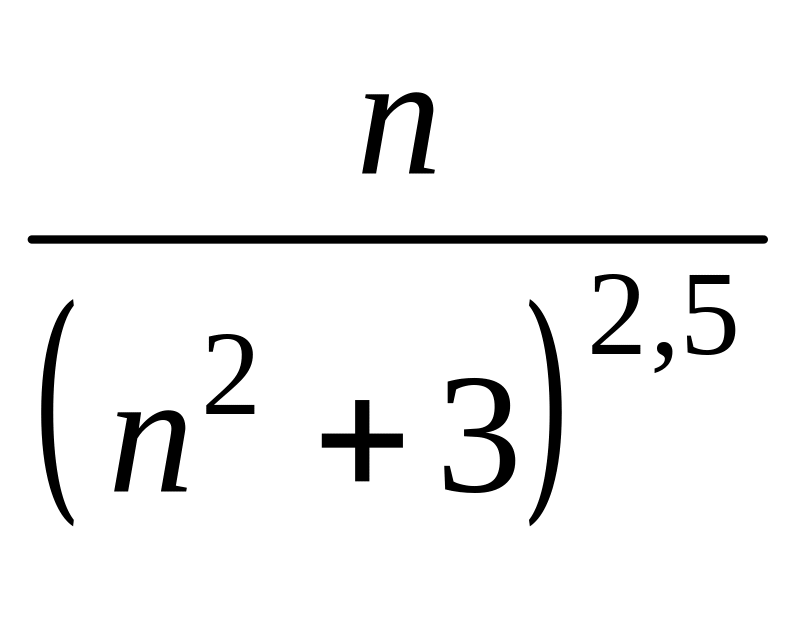Следовательно, ряды ведут себя одинаково. Так как ряд сходится, то по предельному признаку сравнения будет сходиться и ряд .