
- •Рецензент:
- •16.2 Равновесие объекта под действием произвольной
- •16.3 Равновесие объекта под действием произвольной
- •1.Объект. Силы и их классификация
- •1.1 Объект
- •1.2 Силы и их классификация
- •По расположению сил
- •Сходящиеся силы.
- •По месту действия силы
- •По известности
- •По характеру изменения силы
- •Разновидность систем сил
- •2. Аксиомы статики
- •3. Опоры и их реакции
- •4. Действия с силами
- •4.1 Проекции силы на оси
- •4.2 Момент силы относительно точки
- •Теорема Вариньона
- •4.4 Момент силы относительно оси
- •Пара сил и её свойство
- •Приведение силы к новому центру или теорема Пуансо
- •Приведение системы сил к центру
- •Перенесем параллельно в новый центр , точку о. Добавим момент этой силы относительно точки о
- •Перенесем параллельно в новый центр , точку о. Добавим момент этой силы относительно точки о
- •8. Случаи приведения главного вектора системы сил и главного момента всех сил
- •Приведение системы сил к динаме или к двум скрещивающимся силам.
- •9.Инварианты системы сил. Уравнение центральной оси системы сил
- •10. Равновесие объекта под действием системы сил:
- •10.1. Равновесие тела под действием произвольной системы сил в пространстве и на плоскости
- •10.2. Равновесие тела под действием параллельных сил в пространстве и на плоскости
- •10.3. Равновесие тела под действием
- •11. Методика решения задач статики на равновесие тела
- •12. Определение реакций опор составных конструкций
- •13. Трение
- •13.1. Трение скольжения
- •13.2. Трение качения
- •13.3. Трение верчения /к.Т.М. Лойцянский и Лурье/
- •14. Центр тяжести
- •14.1. Приведение двух параллельных сил
- •14.1.2.Приведение системы параллельных сил
- •14.2 Центр тяжести твердого тела
- •14.3.Способы определения положения центра
- •14.4. Центры тяжести некоторых линий,
- •Однородный плоский треугольник
- •Центр тяжести однородной дуги
- •Центр тяжести площади сектора круга
- •15.2 Равновесие объекта под действием произвольной
- •15.3 Равновесие объекта под действием произвольной
9.Инварианты системы сил. Уравнение центральной оси системы сил
Поговорим о главном векторе системы сил. Он не зависит от центра приведения, следовательно,
=const. (I)
Главный вектор системы сил инвариантен к центру приведения.
На рис.
56 а видно
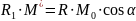 ,
где
,
где
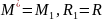 (cм.
случай приведения 5, рис. 58 б).
(cм.
случай приведения 5, рис. 58 б).
Эту запись можно записать в форме скалярного умножения:
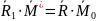 ,
,
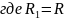
или
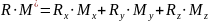 .
(1)
.
(1)
Отсюда получается формула для вычисления наименьшего главного момента
 (2)
(2)
Обозначения
составляющих см. на с.79, формулы (1а),
(2а), где определяли главный вектор
системы сил и главный момент через
проекции на координатные оси. Из формулы
(1) получим значение наименьшего главного
момента
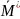 через
проекции главного вектора и главного
момента
,
через
проекции главного вектора и главного
момента
,
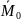 на координатные оси.
на координатные оси.
Если будем выбирать любой центр приведения, то увидим, что
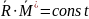 (II)
(II)
Результат показывает, скалярное произведение главного вектора на главный момент данной системы сил инвариантно по отношению к центру приведения.
При приведении системы сил к любой из точек центральной оси получаются две инвариантные величины
и , они представляет собой динаму.
Так как и направлены по одной прямой, то одноименные их проекции пропорциональны:
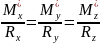 ,
,
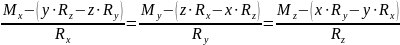
Получили уравнение центральной оси системы сил.
Здесь постоянными величинами являются проекции главного вектора системы сил на координатные оси;
постоянными
величинами являются проекции на те же
оси главного момента системы сил
относительно начала координат
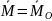 ;
а также наименьший момент
на
те же оси.
;
а также наименьший момент
на
те же оси.
10. Равновесие объекта под действием системы сил:
10.1. Равновесие тела под действием произвольной системы сил в пространстве и на плоскости
Состояние объекта является покой или поступательное прямолинейное движение тела.
Г лавный вектор системы сил, действующих на объект, равен нулю. Главный момент сил, действующих на объект, равен нулю.
(1)
(I)
(2)
где k=1,2,….,n. Формула (I) означает векторную форму записи условия равновесия тела.
Главный вектор системы сил можно записать через её проекции:
, (a)
где , , (1a),
где проекции главного вектора системы сил представлены через алгебраические суммы проекций системы сил на те же координатные оси x, y, z. Следовательно, при равновесии главный вектор сил можно записать через три условия равновесия системы сил на координатные оси
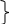
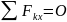 ,
,
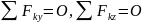 (1*)
(1*)
Главный момент сил относительно заданного центра или вектор-момент главной пары можно записать через проекции по формуле:
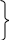
,
или (б)
.
Запишем проекции главного момента как алгебраические суммы моментов системы сил на те же координатные оси
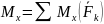 ,
,
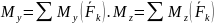 (2б)
(2б)
Следовательно, при равновесии главный момент сил можно записать через три условия равновесия моментов системы сил на координатные оси x, y, z
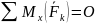 ,
,
 (2*)
(2*)
1.Условия равновесия тела в пространстве под действием произвольной системы сил в координатной форме можно представить:
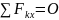
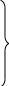
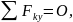

(II)

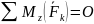 .
.
Получили шесть условий равновесия тела под действием системы сил, т.к. тело в пространстве имеет шесть степеней свободы, которые закрываются. Первые три условия закрывают любые перемещения тела относительно координатных осей x, y, z. Вторая тройка условий равновесия тела закрывают любые повороты его относительно тех же координатных осей
2.Условия равновесия тела в плоскости под действием произвольной системы сил в координатной форме можно представить:

 (III)
(III)
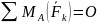
Так как тело в плоскости имеет три степени свободы,
то получили три условия равновесия тела под действием системы сил и три степени свободы закрываются. Первые два условия закрывают любые перемещения тела относительно координатных осей x, y. Третье условие равновесия закрывает любой поворот тела относительно любой точки тела. Получили универсальную форму (III) условий равновесия в плоскости или соновную форму.
Есть еще две формы записи условий равновесия тела в плоскости, но они имеют частный характер и записываются при определенном условии. Рассмотрим их.
СЛУЧАЙ 1. Тело в плоскости находится в равновесии под действием произвольной системы сил.
При этом
ось
 не должна быть перпендикулярна прямой,
проходящей через точки А и В.
не должна быть перпендикулярна прямой,
проходящей через точки А и В.
Тогда система трех условий равновесия записывается:
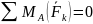 ,
,
 ,
,
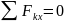 (IV)
(IV)
Покажем, что при этих условиях система сил, произвольно расположенная в пространстве удовлетворяет записи (IV).
Доказательство проведем от противного (см. рис. 63). Пусть система сил приводится к равнодействующей . Моменты этой силы относительно точек А и В равны нулю. Проекция равнодействующей силы на ось, которая перпендикулярна прямой, проходящей через две точки А и В, равна нулю. Тогда появляется противоречие: равновесия нет, но по записи равновесие есть. Следовательно, чтобы не было противоречия необходимо, чтобы выбранная ось х была не перпендикулярна прямой, проходящей через точки А и В, если нет равновесия. При равновесии системы сил равнодействующая на любую ось, например, u должна быть равна нулю:
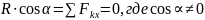
Таким образом, форма записи (IV) справедлива.
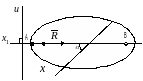
Рис. 63
Случай 2. Тело в плоскости находится в равновесии под действием произвольной системы сил.
При этом точки А, В, С не должны лежать на одной прямой.
Тогда система трех условий равновесия записывается:
,
,
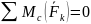 ,
(V)
,
(V)
Покажем, что при этих условиях система сил, произвольно расположенная в пространстве удовлетворяет записи (V).
Доказательство проведем от противного (см. рис. 64).
Пусть система сил приводится к равнодействующей . Моменты равнодействующей силы относительно точек А и В равны нулю. Если бы точка С принадлежала прямой х, на которой находятся точки А и В, то момент равнодействующей силы также был бы равен нулю, что
невозможно, т.к. равновесия нет. В случае не равновесия
системы
сил нужно выбрать точку С не на прямой,
проходящей через точки А и В, тогда
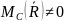
При равновесии системы сил равнодействующая относительно любой точки С , не лежащей на прямой, проходящей через две точки А и В, должна быть равна нулю .
Таким образом, форма записи (V) справедлива.

Рис. 64
