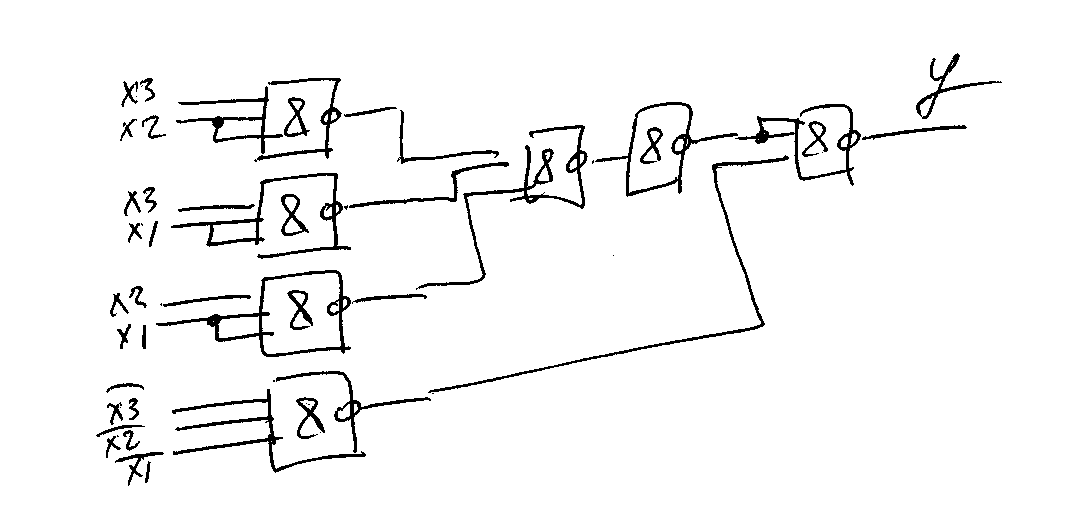
1. Побудувати комбінаційну схему у елементному базисі 3І-НЕ для функції, яка задана у вигляді ДДНФ 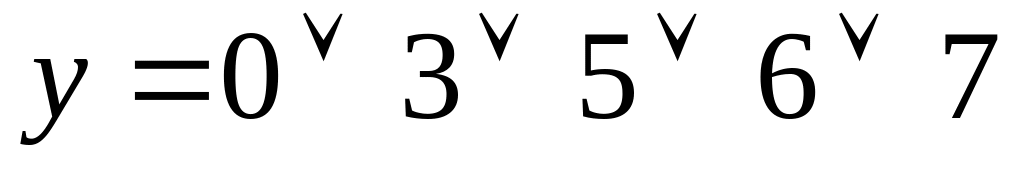.(28 вопрос)

ДДНФ - досконала дез’юнктивна нормальна форма. Спочатку мінімізуємо функцію за допомогою діаграм Вейча. Для цього заповнюємо таблицю відповідно до нашої функції. Це робимо в такій послідовності:

6	7	3	2
4	5	1	0

Х2

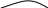
1 Х3	1	1	0
0	1	0	1

Х1

Записуємо терми, враховуючи склеювання сусідніх конституент. Отримуємо мінімізовану функцію в базисі І/АБО. Для приведення її до базису І/НЕ використаємо правило де - Моргана, тобто внесемо функцію під 2 заперечення та використовуємо такі формули:

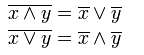
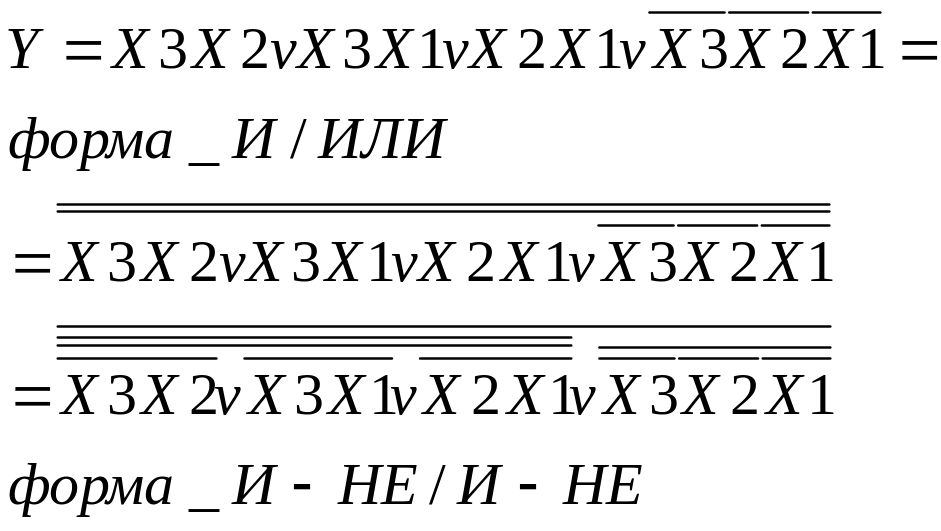
2 . Виконати мінімізацію перемикальної функції методом Квайна .(ПОХОЖ НА 9 ВОПРОС)

Метод Квайна — способ представления функции в ДНФ или КНФ с минимальным количеством членов и минимальным набором переменных.[1][2][3]

Преобразование функции можно разделить на два этапа:

-на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так

называемой сокращённой форме;

-на втором этапе — переход от сокращённой формы к минимальной форме.

Запишемо конституенти 1иці функції у потрібній для нас формі:

0 = 0000₂= X₁X₂X₃X₄

3 = 0011₂= X₁X₂X₃X₄

5 = 0101₂= X₁X₂X₃X₄

6 = 0110₂= X₁X₂X₃X₄

9 = 1001₂= X₁X₂X₃X₄

1 1 = 1011₂= X₁X₂X₃X₄

1 4 = 1110₂= X₁X₂X₃X₄

Виконуємо попарне склеювання конституент одиниці

X ₁X₂X₃X₄ v X₁X₂X₃X₄ = X₁X₂X₃X₄ v X₁X₂X₃X₄ v X₂X₃X₄

X ₁X₂X₃X₄ v X₁X₂X₃X₄ = X₁X₂X₃X₄ v X₁X₂X₃X₄ v X₂X₃X₄

X₁X₂X₃X₄ v X₁X₂X₃X₄ = X₁X₂X₃X₄ v X₁X₂X₃X₄ v X₁X₂X₄

О держали множину імплікант 3-го рангу

X₂X₃X₄ , X₂X₃X₄ , X₁X₂X₄

Подальше склеювання імплікант неможливе. Тоді задана перемикальна функція матиме такий вигляд.

f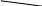 (x1,x2,x3,x4) = X₁X₂X₃X₄ v X₁X₂X₃X₄ v X₁X₂X₃X₄ v X₁X₂X₃X₄ v X₁X₂X₃X₄ v X₁X₂X₃X₄ v

v X₁X₂X₃X₄ v X₂X₃X₄ v X₂X₃X₄ v X₁X₂X₄

Виконавши поглинання за формулою BC v C = C:

f (x1,x2,x3,x4) = X₁X₂X₃X₄ v X₁X₂X₃X₄ v X₂X₃X₄ v X₂X₃X₄ v X₁X₂X₄

Таблиця покриття

Імпліканти	Констатуенти
	V
			V
		V				V
				V			V
					V	V

Знаходимо ядро функцій - сукупність імплікант що відповідають одноразовим покриттям конституент.

3.Виконати мінімізацію перемикальної функції за допомогою діаграм Вейча . Побудувати комбінаційну схему в елементному базисі 3АБО-НЕ.(7 вопрос)

Заповнюємо таблицю Вейча. Значення функції записуємо в клітинки, що відповідають номерам наборів.

Це робимо в такій послідовності:

12	13	10	8
14	15	11	9
6	7	3	2
4	5	1	0

Х3

1 Х4	0	1	0
1	1	1	0 Х2
0	1	0	0
0	0	1	0

Х1

Діаграма Вейча

Отримуємо ДКНФ (мінімізуємо по нулях функції) і за правилом де – Моргана (внесемо функцію під 2 заперечення та використовуємо такі формули:

)

переводимо функцію до базису АБО-НЕ/АБО-НЕ

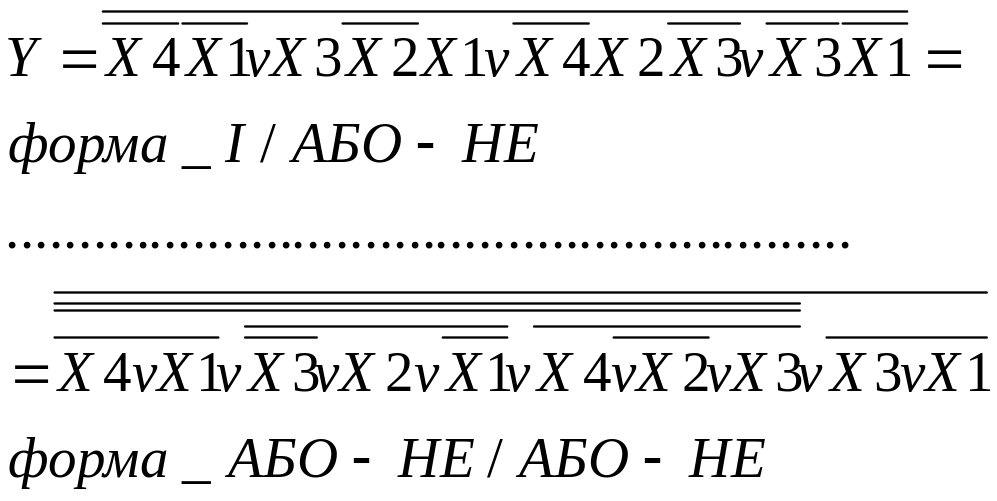
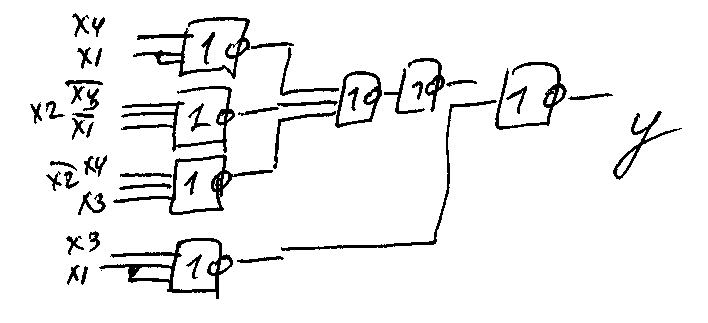
4. Виконати мінімізацію перемикальної функції за допомогою діаграм Вейча .

Побудувати комбінаційну схему в елементному базисі 3І-АБО.(8 вопрос)

Заповнюємо таблицю Вейча. Значення функції записуємо в клітинки, що відповідають номерам наборів.

Це робимо в такій послідовності:

12	13	10	8
14	15	11	9
6	7	3	2
4	5	1	0

Х3

1 Х4	0	1	0
1	1	1	0 Х2
0	1	0	0
0	0	1	0

Х1

Діаграма Вейча

Отримуємо ДДНФ (мінімізуємо по одиницях функції). Функція виражена в базисі І/АБО

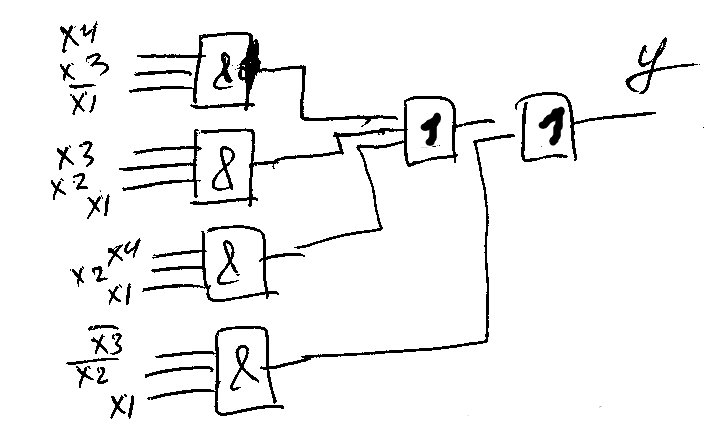
5. Побудувати комбінаційну схему, використовуючи логічні елементи 3І-НЕ, для перемикальної функції що записана в операторній формі .(29 ВОПРОС)

В початковому вигляді функція зображена у базисі І/НЕ/І-НЕ, окрім останнього терму. Отже ми можемо не виконувати ніяких перетворень, а просто добавити ще один елемент І-НЕ для останнього терму.

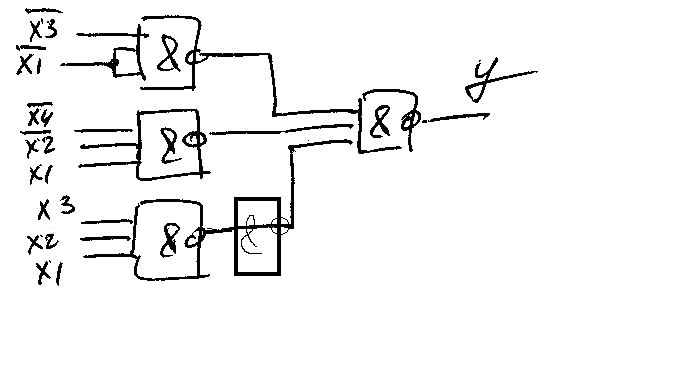
6. Скільки термів містить МДНФ перемикальної функції, що задана у вигляді .(35 вопрос)

Проаналізувати можемо виконавши мінімізацію за допомогою діаграм Вейча.

Для цього заповнюємо таблицю відповідно до нашої функції. Це робимо в такій послідовності:

6	7	3	2
4	5	1	0

Х2

Х3

1	0	1	0
1	1	1	0

Х1

У результаті мінімізації отримуємо МДНФ на 4 терми.

7. Довести чи є функціонально повною система з двох функції АБО та ВИКЛЮЧНЕ АБО.(15 вопрос)

Функционально полной системой булевых функций (ФПСБФ) называется совокупность таких булефых функций (f1, f2, ... fk), что произвольная булева функция f может быть записана в виде формулы через функции этой совокупности. За критерием Поста:Для того чтобы система S булевых функций была функционально полной, необходимо и достаточно, чтобы эта система содержала хотя бы одну булеву функцию, не сохраняющую константу 1, хотя бы одну булеву функцию, не сохраняющую константу 0, хотя бы одну несамодвойственную булеву функцию, хотя бы одну нелинейную булеву функцию и хотя бы одну немонотонную булеву функцию.

Запишемо в таблицю результат виконання даних функцій з операндами

a	b	АБО	V
0	0	0	0
0	1	1	1
1	0	1	1
1	1	1	0

Визначимо приналежність кожної функції кожному з 5 класів Булевих функцій (результати відобразимо в таблиці):

Пять классов

K1 – на нулевом наборе содержит «0»

(К булевым функциям сохраняющим константу 0, относят такие булеы функции f(x1,...,xn), для которых справедливо соотношение f(0,...,0)=0.)

K2 – на единичном наборе содержит «1»

(К булевым функциям сохраняющим константу 1, относят такие булеы функции f(x1,...,xn), для которых справедливо соотношение f(1,...,1)=1.)

K3 – самодвойственность

(Булева функция называется самодвойственной, если на любых двух противоположных наборах она принимает противоположные значения. )

K4 – монотонность

(Булева функция f(x1,...,xn) называется монотонной, если для любых двух наборов Y = <y1,y2,...,yn> и B = <b1,b2,...,bn> таких, что Y >= B имеет место неравенство f(y1,...,yn)>=f(b1,...,bn).)

K5 – линейность

(К линейным булевым функциям относят такие булевы функции, которые представимы в виде f(x1,...,xn)=с0 + c1x1 + ... + cnxn,

где ci E {0,1}, а + операция "сумма по mod 2".)

	K1	K2	K3	K4	K5
АБО	+	+	-	+	-
V	+	-	-	-	-

Вывод: Система не является функционально полной, поскольку не отвечает критерию Поста (нет булевой функции, не сохраняющей константу 0).

8. Довести чи є функціонально повною система з двох функції І-НЕ та АБО.(16 ВОПРОС)

Теорія аналогічна до 15 питання

a	b	АБО	І-НЕ
0	0	0	1
0	1	1	1
1	0	1	1
1	1	1	0

	K1	K2	Kс	Kм	Kн
АБО	+	+	-	+	-
І-НЕ	-	-	-	-	-

Вывод: За критерием Поста система є повною

9. За допомогою логічних елементів І, АБО, НЕ побудувати комбінаційну схему для виразу .(17 ВОПРОС)

11. Спростити вираз .(38 ВОПРОС)

Для спрощення виразу використаємо формули з теореми де –Моргана:

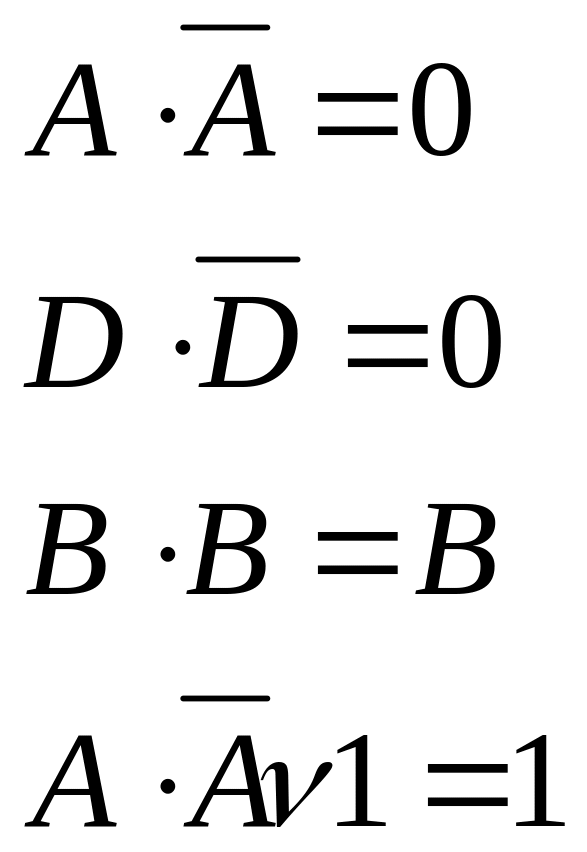
12. Спростити вираз (107 ВОПРОС)

Для спрощення виразу використаємо формули з теореми де –Моргана (останні 3 рядки на сторінці):

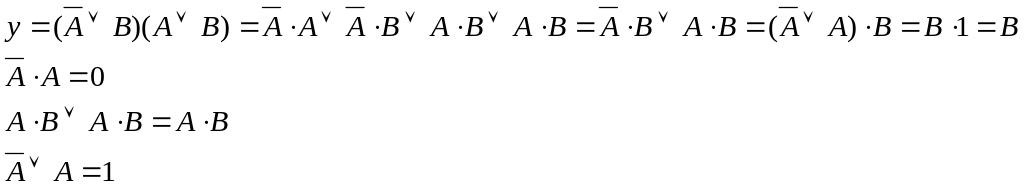
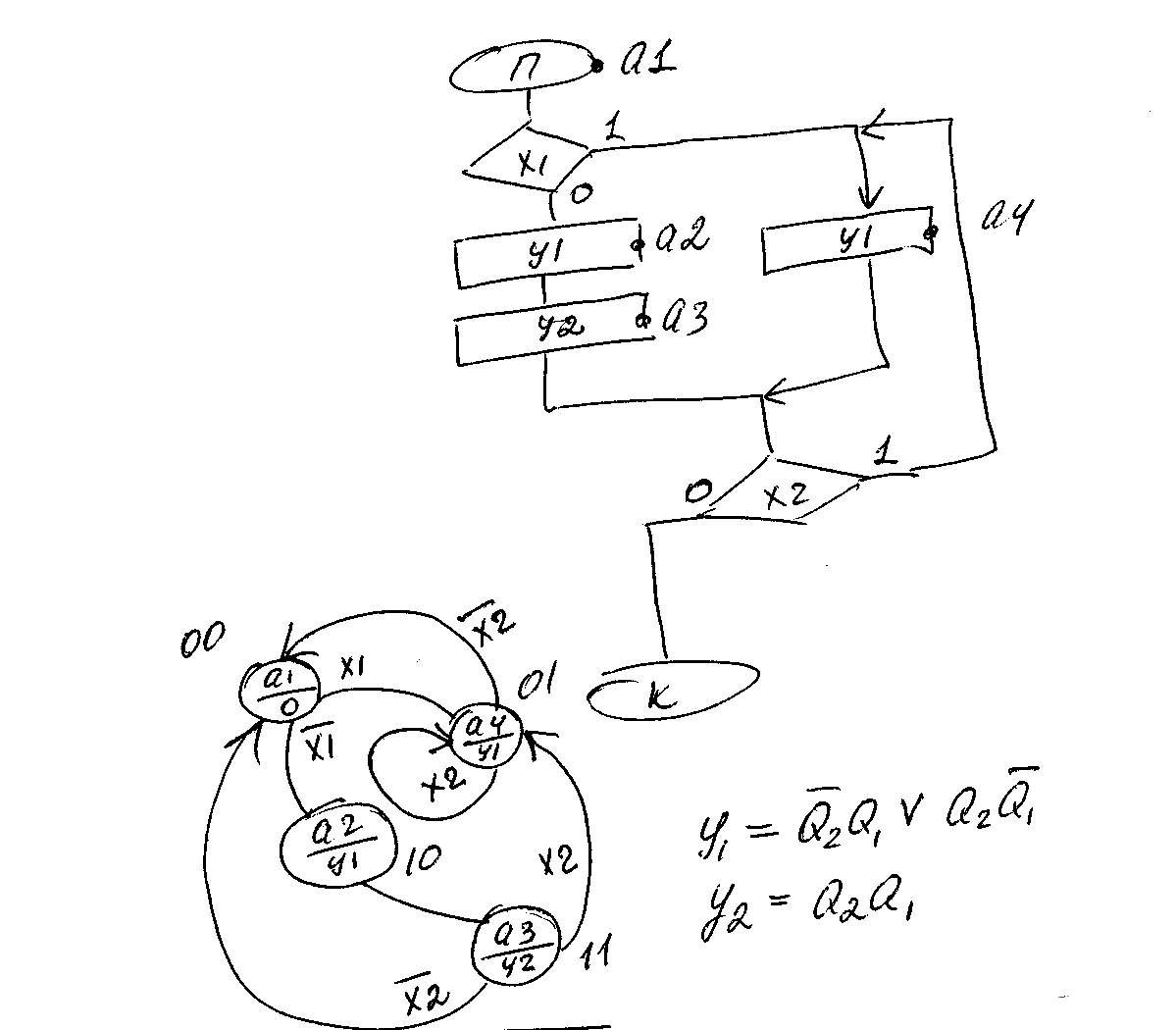
12. За заданою ЛСА побудувати граф автомата Мура, отримати вирази для керуючих сигналів 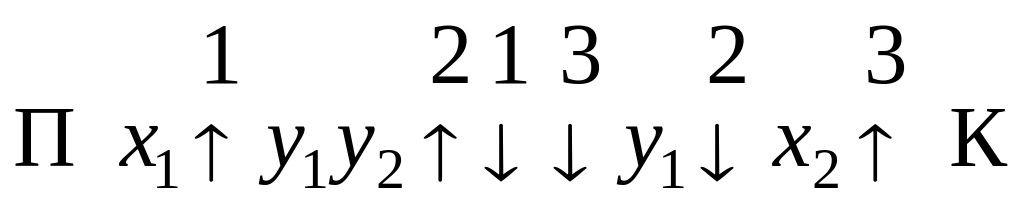.(18 ВОПРОС)

Му́ра автомат — скінченний автомат, вихід якого в даний такт t залежить від його стану в цьому такті і не залежить від його входу, тобто y(t) = λ(g(t)).

Будуємо за ЛСА алгоритм, на якому проводимо розмітку вершин автомата Мура. Автомат є циклічним, тому кінець позначаємо як першу вершину. Також вершинами позначаємо всі оператори, окрім умовних. Далі будуємо граф автомата, у якому відображаються всі можливі переходи по алгоритму. Звідси можемо вивести вирази керуючих сигналів.

13. Скільки тригерів необхідно для побудови цифрового автомату, що має 14 станів?(36 ВОПРОС)

Якщо, наприклад, в автоматі Мура кодувати операторні вершини від 0(0000) до 14(1110), то бачимо, що потрібно мати 4 тригери, тобто 2 в 4 степені = 16, нам вистачає 4 тригера, щоб закодувати 14 станів (максимум 16)

14. Зробити розмітку станів автомата Мілі і побудувати граф автомата, якщо задано ЛСА 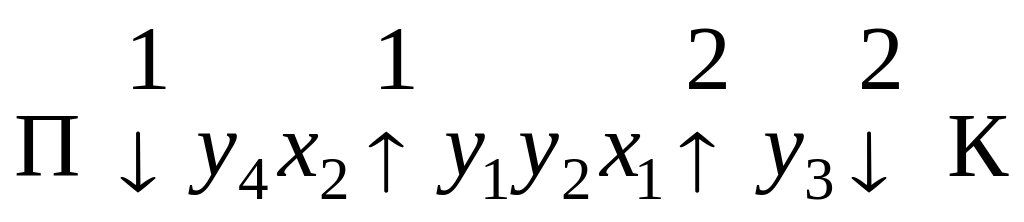.(19 вопрос)

Автомат Мили (англ. Mealy machine) — конечный автомат, выходная последовательность которого (в отличие от автомата Мура) зависит от состояния автомата и входных сигналов. Это означает, что в графе состояний каждому ребру соответствует некоторое значение (выходной символ). В в вершины графа автомата Мили записываются выходящие сигналы,а дугам графа приписывают условие перехода из одного состояния в другое,а так же входящие сигналы. Кодировка автомата Мили: Вершина (операторная или логическая),стоящая после вершины "Начало" ,а так же вход вершины "Конец" помечается символом А1,вершины,стоящие после операторных помечаются символом Аn (n=2,3..).

А1

А2

А3

А4

А1

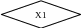
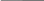
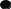
1

0

1

0

19. Подайте десяткове число Х= – 92,623 у двійковій системі числення із точністю до 10-го розряду після коми і поданням значення знакового розряду.(30 ВОПРОС)

Цілу частину у двійкову систему переводимо діленням на 2, з урахуванням остачі.

Ціла частина

Число	Частка	Остача
92/2=	46	0
46/2=	23	0
23/2=	11	1
11/2=	5	1
5/2=	2	1
2/2=	1	0
1/2=	-	1

92₁₀ = 1011100₂

Дробову частину у двійкову систему переводимо множенням на 2, з фіксацією одиниці у цілій частині після операції множення.

Дробова частина

0,623*2=	1,246	1
0,246*2=	0,492	0
0,492*2=	0,984	0
0,984*2=	1,968	1
0,968*2=	1,936	1
0,936*2=	1,872	1
0,872*2=	1,744	1
0,744*2=	1,488	1
0,488*2=	0,976	0
0,976*2=	1,952	1

0,62310 = 0,1001111101₂

В прямому коді:

– 92,623₁₀ = 1 1011100, 1001111101₂

19. Подайте задане двійкове число у прямому та доповнювальному машинних кодах, якщо ширина розрядної сітки дорівнює 10-и розрядам: Х= – 0,0111001.(31 ВОПРОС)

Прямой код — способ представления двоичных чисел с фиксированной запятой в компьютерной арифметике. Главным образом используется для записи положительных чисел.

При записи числа в прямом коде старший разряд является знаковым разрядом. Если его значение равно 0 — то число положительное, если 1 — то отрицательное. В остальных разрядах (которые называются цифровыми разрядами) записывается двоичное представление модуля числа.

Дополнительный код (англ. two’s complement, иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение).

В прямому коді:

1 011100100

Доповнювальний код отримуємо з прямого, шляхом його інвертування та додавання одиниці.

В доповняльному коді:

1 100011100

19. Виконайте додавання двійкових чисел С = А+В (де |A|<0, |B|<0) у доповнювальному коді, якщо А = –00,01101, В = + 00,10011. Проаналізуйте знак результату.(6 ВОПРОС)

Дополнительный код (англ. two’s complement, иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение).

Ад = 11,10011;

Вд = 00,10011;

11,10011

00,10011

100,00110

С = 00,00110.

Знак результату – додатній.

19. Подайте задане двійкове число у прямому та зворотному машинних кодах, якщо ширина розрядної сітки дорівнює 11-и розрядам: Х= – 0,010011.(32 ВОПРОС)

Прямой код — способ представления двоичных чисел с фиксированной запятой в компьютерной арифметике. Главным образом используется для записи положительных чисел.

При записи числа в прямом коде старший разряд является знаковым разрядом. Если его значение равно 0 — то число положительное, если 1 — то отрицательное. В остальных разрядах (которые называются цифровыми разрядами) записывается двоичное представление модуля числа.

Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения над натуральными числами. Обратный n-разрядный двоичный код положительного целого числа состоит из одноразрядного кода знака (двоичной цифры 0), за которым следует n − 1-разрядное двоичное представление модуля числа (обратный код положительного числа совпадает с прямым кодом). Обратный n-разрядный двоичный код отрицательного целого числа состоит из одноразрядного кода знака (двоичной цифры 1), за которым следует n − 1-разрядное двоичное число, представляющее собой инвертированное n − 1-разрядное представление модуля числа.

Хпр = 10100110000

Хзв = 11011001111

19. Виконайте додавання двійкових чисел Z = X+Y (де |X|<0, |Y|<0), якщо X = – 00,01101, Y = – 00,10011. Проаналізуйте знак результату.(5 ВОПРОС)

Додавання виконаємо в доповнювальному коді:

Дополнительный код (англ. two’s complement, иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение).

Xд = 11,10011;

Yд = 11,01101;

11,010011

11,001101

11,100000

Z = 11,100000 .

Знак результату – від’ємний.

24. Сформулювати визначення перемикальної функції, логічного елементу та комбінаційної схеми. Наведіть приклади.(39 ВОПРОС)

Функція у = f(x1,x2,…,x_n) називається перемикальною, або логічною, якщо сама функція у і кожен з її аргументів х_і , приймають значення тільки із множини {0,1}.

Перемикальна функція може бути задана різними способами, наприклад:

• Словесним описом

• Таблицею істинності

• Геометричним представленням

• Аналітичним виразом.

Логічний елемент – це електронна схема, що реалізує певну перемикальну функцію. На функціональних схемах логічний елемент зображується за допомогою умовного графічного позначення (УГП).

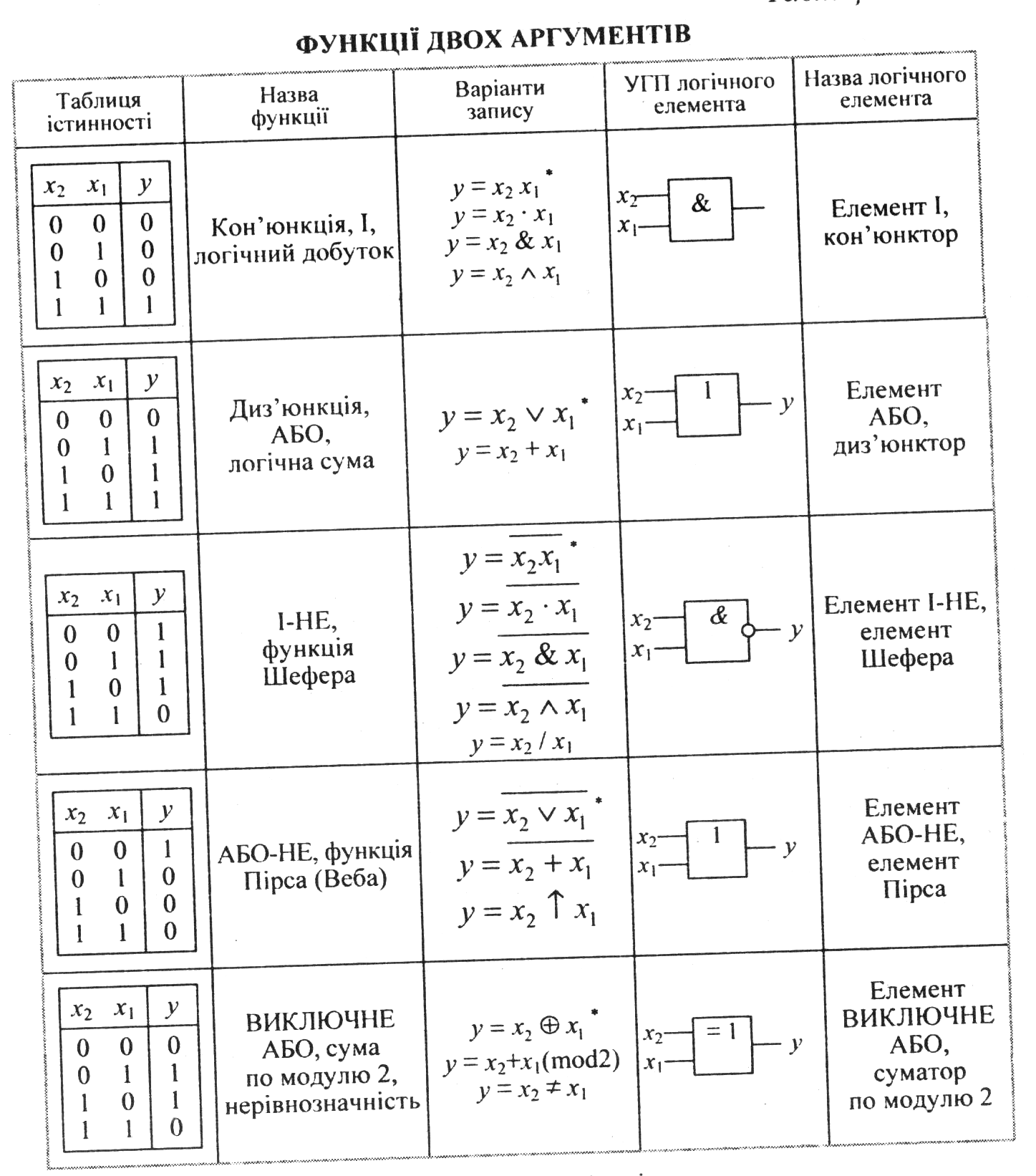
Під комбінаційною схемою розуміють таку схему, функціонування якої може бути описане системою перемикальних функцій.

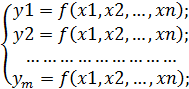
Де n кількість входів а m кількість виходів схеми

Приклад комбінаційної схеми:

&

&

1

Х1

Х2

у

Х3

Х4

25. Сформулюйте визначення дднф та дкнф перемикальної функції. Як отримати операторну форму запису перемикальної функції у заданому елементному базисі. Наведіть приклад.(40 вопрос)

Досконала диз’юнктивна нормальна форма (ДДНФ) і досконала кон’юнктивна нормальна (ДКНФ) форма – універсальні (канонічні) форми аналітичного подання довільної булевої функції.

ДДНФ являє собою диз’юнкцію мінтермів (конституент 1), для яких функція дорівнює одиниці.

ДКНФ являє собою кон’юнкцію макстермів (конституент 0), для яких функція дорівнює 0.

ДДНФ і ДКНФ можна побудувати безпосередньо з таблиці істинності.

X1	X2	F
0	0	0
1	0	1
0	1	0
1	1	1

ДДНФ

ДКНФ

Операторна форма перемикальної функції враховує тип логічних елементів і кількість входів елемента. Для побудови операторної форми при виконані операції з m змінними, коли логічний елемент має g входів (g<m), змінні об’єднують в групи, так щоб в кожну групу входило не більше g змінних.

Операторна форма запису перемикальної функції в базисі 2І-НЕ.

26. Охарактеризуйте основні етапи синтезу комбінаційних схем. Як визначити складність і швидкодію комбінаційних схем?(27 ВОПРОС)

Синтез комбінаційних схем у заданому елементному базисі можна розбити на три етапи:

На першому етапі виконують мінімізацію перемикальних функцій обраним методом.

На другому етапі функції подають у можливих операторних формах, тобто у вигляді суперпозиції операторів заданих логічних елементів.

На третьому етапі з урахуванням цільової функції проектування обирають операторну форму перемикальної функції і будують комбінаційну схему.

Складність комбінаційних схем доцільно визначати за Квайном, або за числом умовних логічних елементів.

Швидкодія комбінаційних схем залежить від часових параметрів логічних елементів, що характеризують затримку сигналів елементами.

27. Нарисуйте узагальнену структурну схему керуючого автомата. Напишіть вирази, що визначають закон функціонування автоматів Мілі і Мура. У чому відмінність автоматів Мілі і Мура?(25 вопрос)

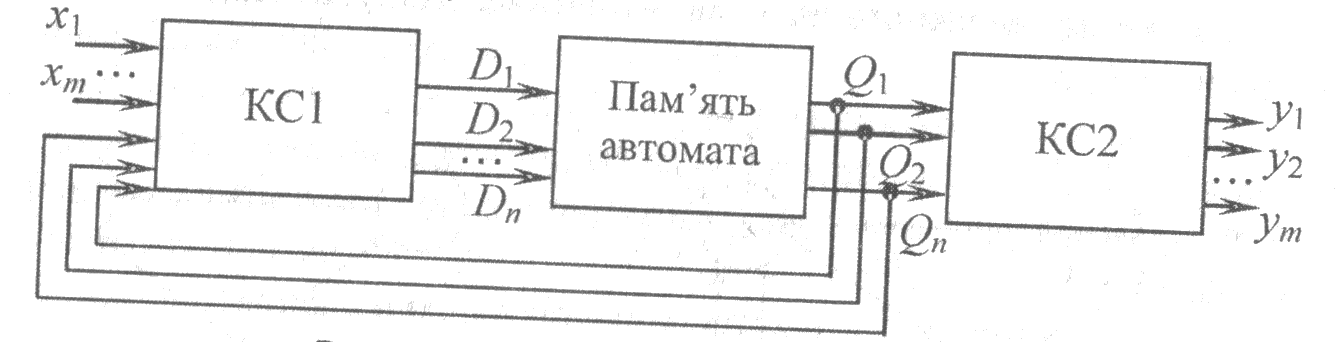
Структурна схема керуючого автомата.

КС1 – комбінаційна схема для вироблення функцій збудження.

КС2 – комбінаційна схема для формування вихідних керуючих сигналів.

Пам’ять автомата – тригери, які зберігають код стану автомата.

Автомат задають сукупністю таких об’єктів: {X,Y,Z,δ, λ,z₀}

X - множина вхідних сигналів;

Y - множина вихідних сигналів;

Z - множина станів автомата;

δ - функція переходів;

λ - функція виходів;

z₀ – початковий стан автомата.

Функція переходів автомата:

Z(t) – стан автомата;

Z(t-1) – попередній стан автомата;

Функції виходів:

Для автомата Мілі:

Для автомата Мура:

В автоматі Мілі вихідні сигнали є функцією вхідних сигналів і стану пам’яті. В автоматі Мура вихідні сигнали визначаються тільки станом пам’яті.

28. Охарактеризуйте основні етапи проектування цифрового автомата. Як здійснюється розмітка станів автомата для автоматів Мілі та Мура? Як побудувати граф автомата? (26 вопрос)

Основні етапи проектування цифрового автомата:

1. Розробка мікропрограми операції.

2. Побудова змістовного графа мікропрограми.

3. Побудова закодованого графа мікропрограми.

4. Розмітка закодованого графа мікропрограма.

5. Побудова графа автомата.

6. Кодування станів пам’яті.

7. Розробка функцій збудження та функцій виходу.

8. Побудова комбінаційних схем функцій збудження і виходу.

Розмітка станів:

Для автомата Мура:

Символом а₁ позначають вершини «початок» і «кінець». Всі інші вершини позначають символами а₂ …а_n, де n – максимальне число станів пам’яті. Кожному стану присвоюють набір вихідних сигналів.

Для автомату Мілі:

Символом а₁ позначають вихід вершини «початок» та вхід вершини «кінець». Виходи операторних вершин позначають символами а₂ …а_n, де n – максимальне число станів пам’яті.

Побудова графа автомата:

Для автомату Мілі:

Зображують N вершин графа – а₁…а_N. Шлях між двома вершинами включає одну операторну і довільне число умовних вершин і зображується орієнтовною дугою. Між двома вершинами може бути декілька шляхів. Біля дуги записують довільне число сигналів х, які записані в умовних вершинах. Біля дуги записують перелік керуючих сигналів.

Для автомата Мура:

Зображують N вершин графа – а₁…а_N. Шлях між двома вершинами зображується орієнтовною дугою. На дугах графа записують сигнали логічних умов. Сигнали керування записують біля вершин графа.