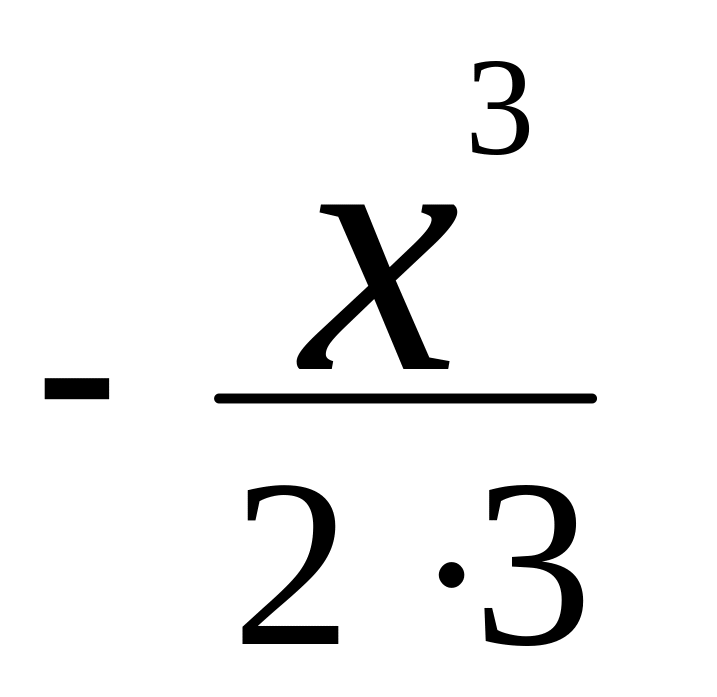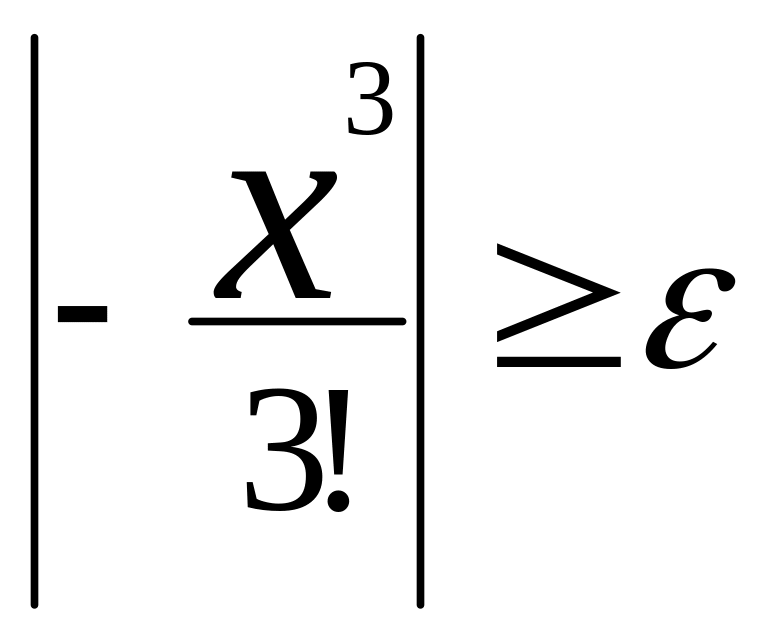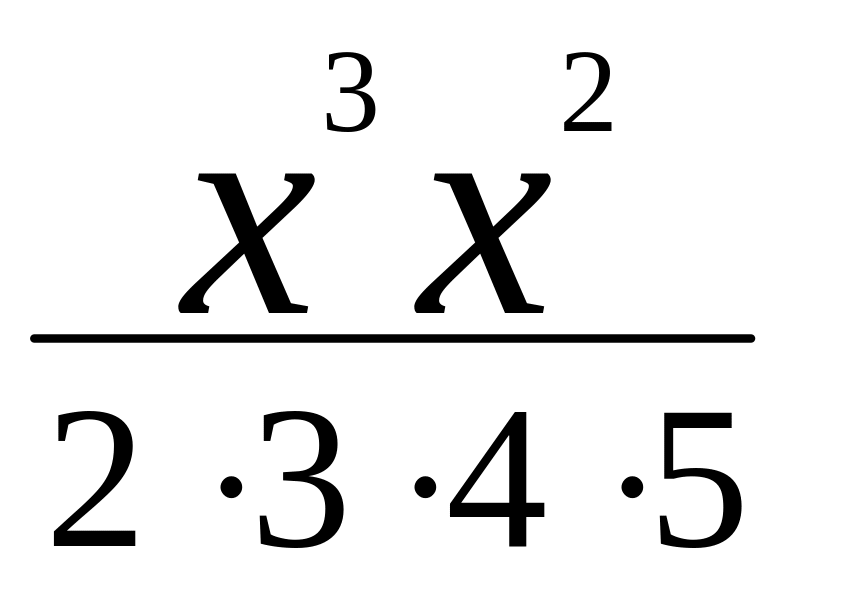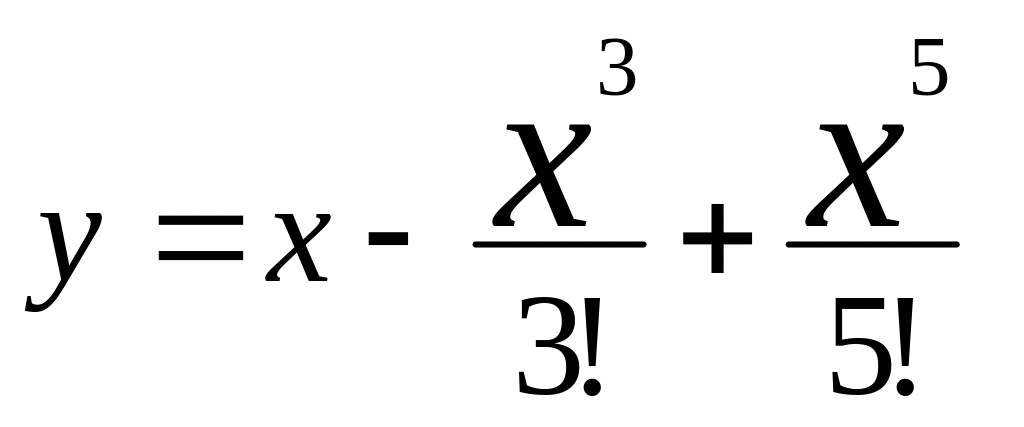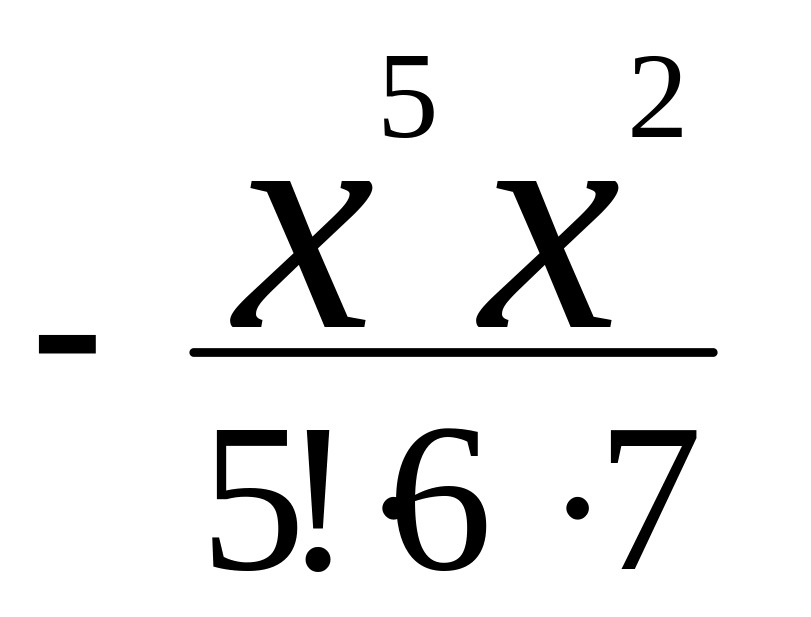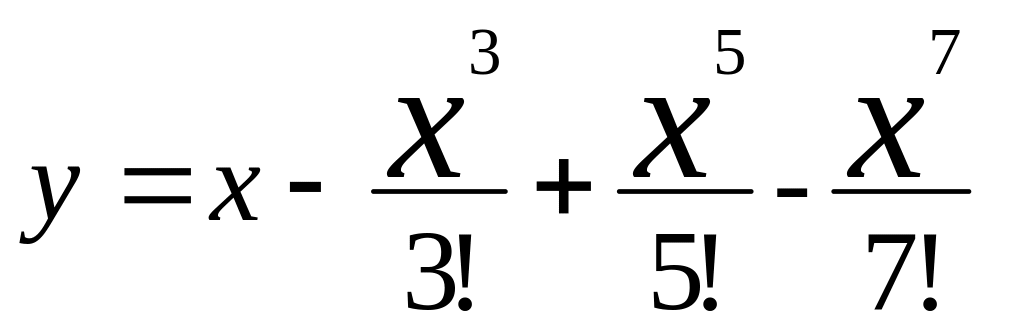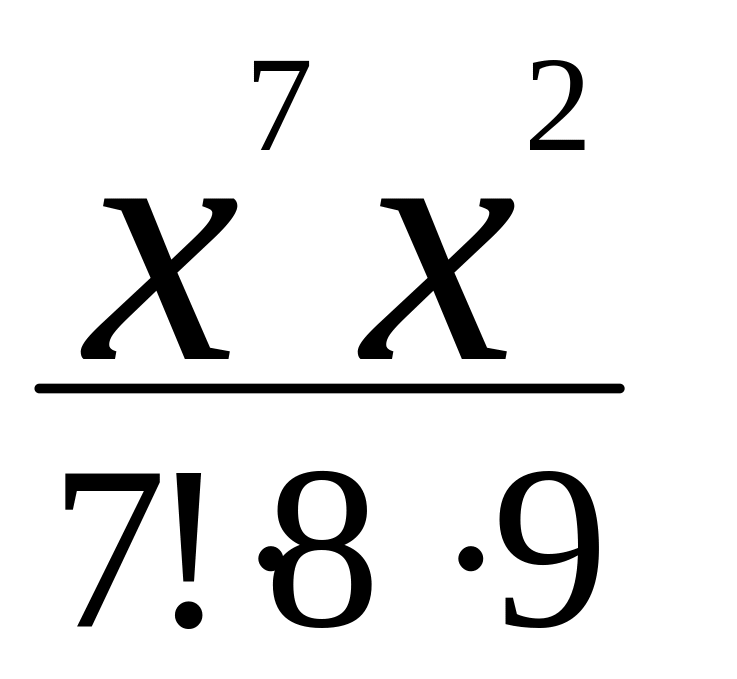1.3. Выбор типа общего члена суммы (произведения) при вычислении сумм и произведений в цикле

Еще несколько замечаний относительно вычисления сумм и произведе­ний в цикле. При нахождении сумм и произведений вида (8.5) и (8.6), соответственно, каждое слагаемое суммы (сомножитель произведения) за­висит от параметра x и номера k, определяющего место этого слагаемого в сумме (сомножителя в произведении).

Обычно формула общего члена суммы (произведения) принадлежит к од­ному из следующих трёх типов:

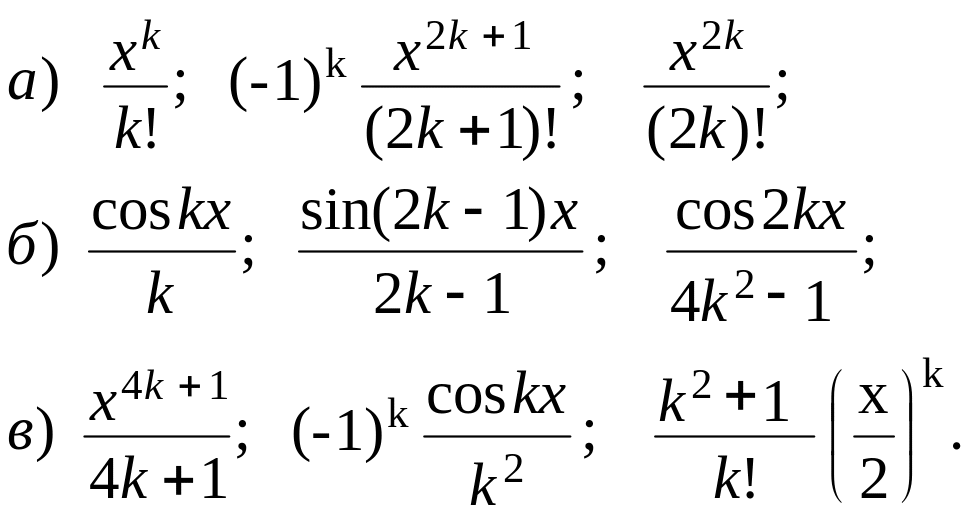
В случае (а) для вычисления члена суммы (произведения) целесооб­разно использовать рекуррентные соотношения, то есть выражать после­дующий член суммы (произведения) через предыдущий. Это позволит су­щественно сократить объем вычислительной работы. Кроме того, вычис­ление члена суммы (произведения) по общей формуле в ряде случаев не­возможно (например, из-за наличия к!.

В случае (б) применение рекуррентных соотношений нецелесообразно. Вычисления будут наиболее эффективными, если каждый член суммы (про­изведения) вычислять по общей формуле.

В случае (в) член суммы (произведения) целесообразно представить в виде двух сомножителей, один из которых вычисляется по рекуррент­ной формуле, а другой – непосредственно. Например, если , то полагаем и вычисляем рекуррентно , а 1/(4k+1) – непосредственно.

1.4. Вывод рекуррентных формул

При алгоритмизации ИЦВП для того, чтобы избежать повторения одних и тех же вычислений стремятся выразить (связать) выражения последу­ющей итерации через выражения предыдущей итерации по определенной ре­куррентной (итерационной) формуле.

Рекуррентная формула – формула, выражающая каж­дый член последовательности а_k (k = 1, 2, … ) через р предыдущих членов вида:

а_k = f(k, a_k-1, а_k-2, … , а_k-р), k ≥ р + 1.

При помощи этой формулы, зная р первых членов последовательности, можно определить всю последовательность, то есть вычислить любой на­перед заданный член последовательности. Этот прием оказывается полез­ным при программировании многих задач. Примерами рекуррентных формул являются уже приведенные формулы Ньютона (8.1) для вычисления прибли­женного значения квадратного корня из числа X и формулы для накопле­ния сумм и произведений в цикле.

Организация многошагового вычислительного процесса при использова­нии одной и той же рекуррентной формулы позволяет сохранять предыду­щие значения в полях памяти ЭВМ только до тех пор, пока не будут вы­числены заменяющие их последующие значения, в том числе и окончатель­ный результат. Это экономит память ЭВМ.

Использование рекурсии в алгоритмах таких задач, как вычисление сумм (произведений) конечного числа слагаемых (сомножителей) или бесконечных рядов, уточнение корней нелинейных уравнений, вычисление наибольшего (наименьшего) из множества значений, позволяет органи­зовать алгоритмы циклической структуры и тем самым добиться сокра­щения записи алгоритма.

В некоторых же случаях разработанные вычислительные приемы (по­добно формуле Горнера для определения значений степенных многочле­нов или рекуррентным формулам для вычисления значений ряда) пред­ставляют возможность максимально использовать циклические свойства формул и в целях сокращения объема вычислений.

Вывод рекуррентных формул для ИЦШ рассмотрим на конкретном при­мере.

Пример 8.7

Составить блок-схему алгоритма определения значения функции y = sin х для заданного х (0 ≤ х ≤ /4), воспользовав­шись степенным разложением

с точностью

Вычисление функции y = sin x с помощью степенного ряда можно представить в виде

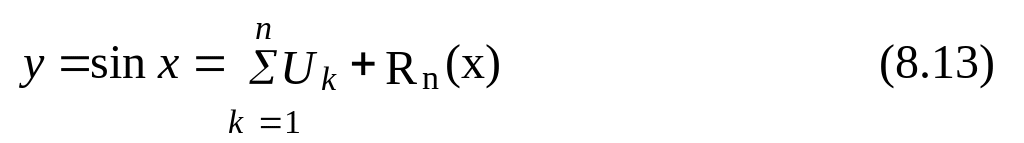
где R_n (х) – остаток ряда, представляющий ошибку (точность) вычис­лений.

Для того, чтобы вывести рекуррентную формулу, необходимо выразить k-й (U_k) и k-1 (U_k-1) члены рассматриваемого степенного ряда и определить их отношение (разность). Для ряда (8.11) k-й и k-1-й члены ряда задаются выражениями

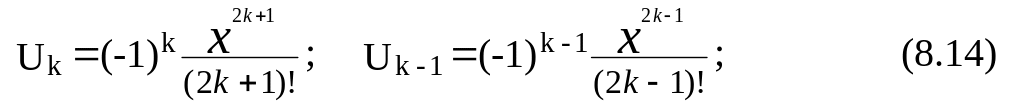
а их отношение (разность)

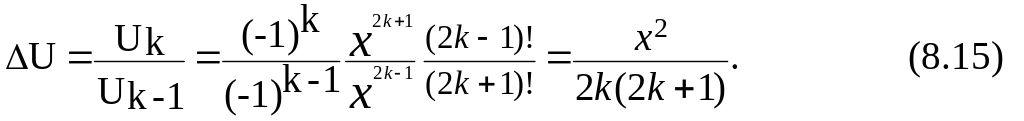
Следовательно, рекуррентная (итерационная) формула для вычисления значений степенного ряда

Поскольку при k = 0, U = - , то k = 1, 2, … . Следова­тельно, с помощью полученного рекуррентного выражения можно опреде­лить члены, начиная не с k = 0, а только c k = 1. Тогда, чтобы оп­ределить первые члены ряда , необходимо задать на­чальные значения для первой итерации:

k = 1; U_k-1 = U₀ = x.

Из полученной формулы (8.16) видно, что при определении значения (2к+1)!, входящего в k-й член ряда, используется значение (2к-1)!, вычисленное для получения U_k-1 . Если независимо произвести вычисле­ние членов ряда, то приходится выполнять множество одинаковых дейст­вий по определению факториалов и возведению в степень переменной х.

Так как в промежутке (0, /4) ряд (8.11) знакочередующийся с монотонно убывающими по модулю членами, то для его остатка справед­лива оценка

поэтому процесс суммирования членов ряда (8.11) может быть прекращен, как только очередной вычисленный член ряда U_k будет по модулю мень­ше допустимой погрешности . В противном случае вычисление очеред­ного k-го члена ряда по итерационной формуле (8.16) продолжается.

Поскольку вычисление значения функции у = sin х сводится к накап­ливанию (суммированию) членов степенного ряда (8.11), то используется уже знакомая рекуррентная (итерационная) формула для накапливания суммы

Y_k = Y_k-1 + U_k (k =1, 2, ... ), (8.18)

при этом следует помнить правило накапливания сумм в цикле: пере­менной, с помощью которой будет накапливаться сумма, необходимо за­дать начальное значение нуль для первой итерации:

k = 1; Y_k = Y₀ =0 (либо Y_k-1 = Y₀ = х).

Таким образом, чтобы запрограммировать итерационные процессы, как правило, требуется знать:

– рекуррентную (итерационную) формулу;

– начальное значение нулевой (в ряде случаев первой) итерации;

– условие прекращения итерационного процесса (необходимо только в случае неизвестного заранее числа итераций (циклов)).

Для рассматриваемого нами примера имеем:

­– рекуррентную (итерацион­ную) формулу для вычисления членов ряда

– начальное значение для первой (нулевой) итерации формулы (8.20)

Y_k-1 = Y₀ = х (при k = 1) (8.20)

– условие прекращения итерационного процесса

– рекуррентную (итерационную) формулу для накопления суммы

Y_k = Y_k-1 + U_k (8.22)

– начальное значение для первой (нулевой) итерации но формуле (8.22)

Y_k-1 = Y₀ = 0 (при k =1) (8.23)

Формулы (8.19, 8.21, 8.22) справедливы для всех k = 1, 2, ..., n (при этом значение n заранее неизвестно).

В результате вычислений по формулам (8.19  8.23) число

приближенно дает искомый результат у = sin х.

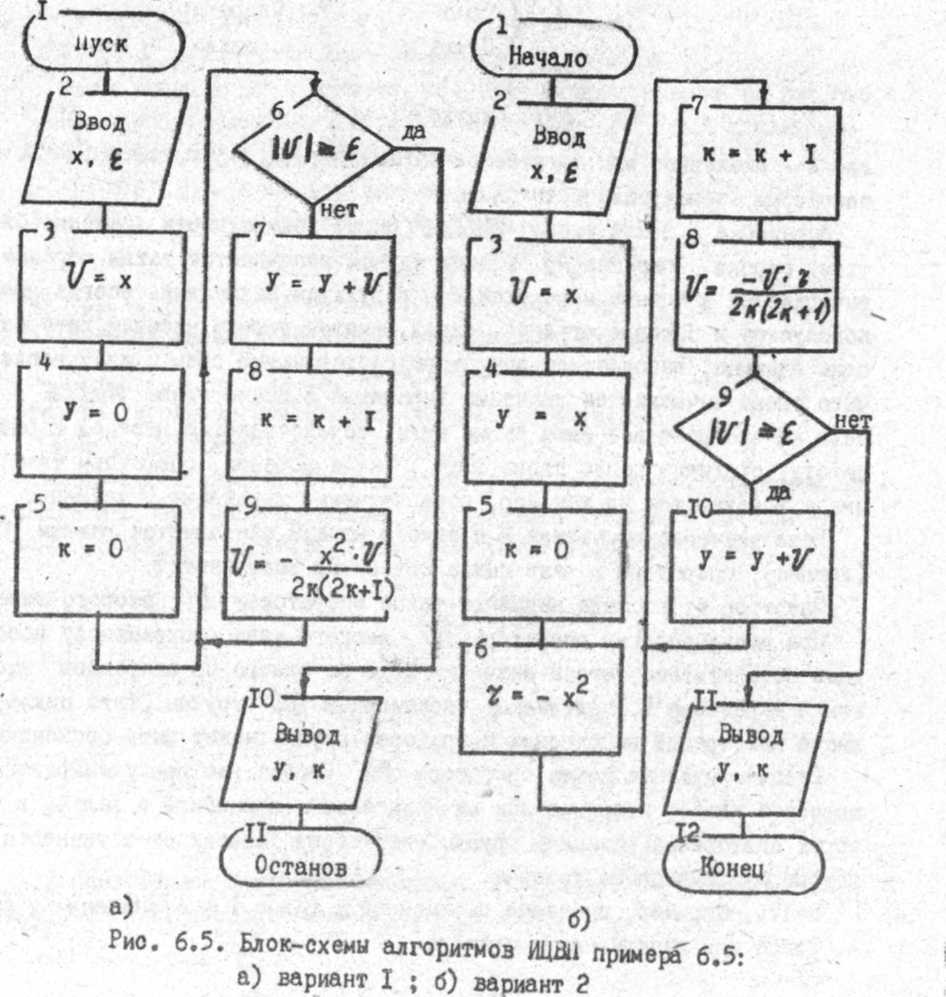
С учетом формул (8.19  8.23) блок-схема ИЦВП вычисления значения функции у = sin х разложением в степенной ряд по двум вариантам по­казана на рис. 8.5.

Проанализируем действительность блок-схемы алгоритма на примере первого варианта, систематизировав основные самостоятельные этапы вы­числений в виде таблицы 8.5.

Таблица 8.5

Основные этапы итерационного вычисления функции у = sin х

Значение k	Значение U	Вид соотношения	Соблюдение соот-	Вид оператора
(блок 8)	(блок 9)	|U| ≥  (блок 6)	ношения блока 6	y = y + U (блок 7)
1			Да
2			Да
3			Да
4			Нет (выход из цикла)

Из таблицы 8.5 видно, что действия, задаваемые блок-схемой примера 8.7, соответствуют логике алгоритма вычисления суммы степенного ряда этого примера.

а)	б)

Рис. 8.5 Блок-схемы алгоритмов ИЦВП примера 8.5: