§8. Доказательство сходимости рядов Фредгольма

С помощью теоремы Адамара мы можем теперь доказать сходимость рядов 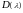и .

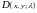а) Сходимость ряда .

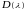выражается рядом

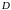
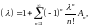(14)(8.1)

где

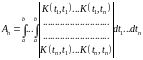
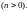_{(15) (8.2)}

Ранее мы предполагали, что . Тогда определитель, входящий в 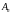, удовлетворяет всем условиям теоремы Адамара, поэтому

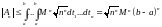
и, следовательно,

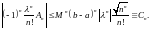
Покажем теперь, что ряд с общим членом сходится. Применяя известный критерий сходимости по Даламберу, находим

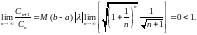
Поэтому ряд с общим членом 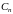сходится, следовательно, ряд сходится абсолютно при всех . Мы запишем этот результат в виде следующей леммы:

Теорема 3. Степенной ряд абсолютно сходится при всех значениях параметра .

б) Сходимость ряда .

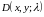Имеем

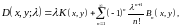(16)(8.3)

где

(17)(8.4)

Формулу (8.3) иногда удобнее писать

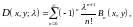
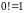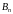где мы полагаем и . Определитель, входящий в , удовлетворяет всем условиям теоремы Адамара, поэтому

,

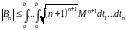
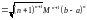откуда

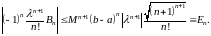
Докажем теперь, что ряд с общим членом сходится. Применяя тот же критерий сходимости, что и в предыдущем случае, находим

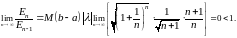
Поэтому ряд с общим членом 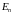сходится, и, значит, ряд абсолютно и равномерно сходится при всех значениях относительно всех и 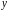, находящихся в области 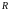. Таким образом, мы имеем следующую лемму:

Теорема 4. Ряд абсолютно и равномерно сходится при всех значениях параметра 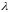в области .

§9. Решение интегрального уравнения, данное Фредгольмом при . Первая фундаментальная теорема Фредгольма

Фундаментальные соотношения Фредгольма, т.е. формулы (7.10) и (7.11), позволят нам теперь получить решение интегрального уравнения для любых .

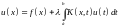. (9.1)

Наведением на метод решения этого интегрального уравнения служит метод решения конечной системы линейных алгебраических уравнений

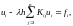
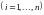. (9.3)

Как известно, для нахождения 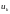из этой системы уравнений каждое уравнение умножают на 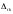и затем все их складывают, т.е. суммируют по 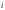от 1 до . Тогда получается:

,

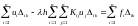откуда

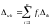. (9.4)

Но теперь, по определению (см. § 7, в),

,

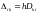и по формуле (6.7)

.

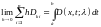Это естественно наводит на мысль аналогичным образом поступить с нашим интегральным уравнением (9.1). Напишем его в форме

.

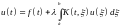Предполагая, что это уравнение удовлетворяется для некоторой непрерывной функции 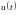, помножим обе его части на 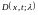и проинтегрируем затем по в пределах от a до 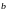. Тогда мы получим

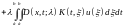. (22)(9.5)

Подынтегральное выражение в двойном интеграле непрерывно относительно и 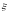, поэтому мы можем переменить порядок интегрирования и написать этот двойной интеграл так

,

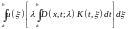что по формуле (7.10) переходит в

.

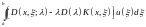Поэтому формулу (9.5) можно написать в виде

,

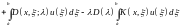что согласно уравнению (9.1) приводится к

.

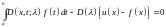Разрешая теперь это уравнение относительно в предположении, что 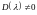, мы получаем

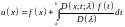. (23)(9.6)

Таким образом, если и есть непрерывная функция от , удовлетворяющая уравнению (9.1), и если , то выражается формулой (9.6).

Нам остается показать, что и, обратно, функция , определяемая формулой (9.6), является решением уравнения (9.1). В этом можно убедиться простой подстановкой. Подставляя значение из формулы (9.6) в уравнение (9.1), получаем

.

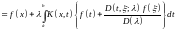Разбивая последний член на две части и меняя порядок интегрирования в двойном интеграле, находим

,

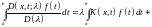
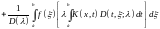что, согласно формуле (7.11) может быть написано в виде

.

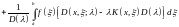Но последнее уравнение, как в этом нетрудно убедиться, представляет собой на самом деле тождество. Следовательно, функция , выражаемая формулой (9.6), действительно удовлетворяет уравнению (9.1).

Таким образом, мы доказали следующую теорему, называемую первой фундаментальной теоремой Фредгольма.

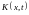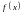Теорема 5. Если ,ядро непрерывно в , функция непрерывна в , то уравнение (9.1) имеет только одно непрерывное решение, оно выражается формулой (9.6), где и 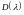– степенные ряды, сходящиеся при всех значениях параметра , а ряд , кроме того, сходится равномерно по и в области .

Пример 5. Найти решение интегрального уравнения

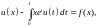
_{вычислив} и

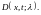
_{Решение. Воспользуемся формулой (9.6),предварительно} вычислив по формулам (8.2) и (8.4) 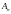и

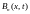
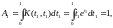
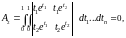
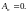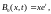
_очевидно, что и все последующие Далее имеем 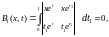очевидно, что и все последующие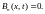

По формулам (8.1) и (8.3) вычисляем и

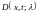
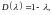
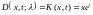
_{и решение уравнения по формуле (9.6) запишется}

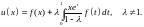
В частности, для 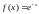получим