- •010400.62 «Прикладная математика и информатика»
- •Введение
- •§1. Классификация интегральных уравнений
- •§2. Решение интегральных уравнений Фредгольма методом последовательных приближений
- •§3. Уравнения с вырожденными ядрами
- •§4. Решение интегральных уравнений Фредгольма с помощью ряда Неймана
- •§5. Итерированные ядра и резольвента интегральных уравнений Фредгольма
- •§6. Решение линейных интегральных уравнений Фредгольма второго рода методом последовательных подстановок
- •§7. Уравнение Фредгольма как предел системы конечного числа линейных алгебраических уравнений. Фундаментальные соотношения Фредгольма
- •§8. Доказательство сходимости рядов Фредгольма
- •§9. Решение интегрального уравнения, данное Фредгольмом при . Первая фундаментальная теорема Фредгольма
- •20…§10. Решение однородных интегральных уравнений. Вторая фундаментальная теорема Фредгольма
- •Вторая фундаментальная теорема Фредгольма
- •И их вычисление
- •§12. Вычисление собственных значений и собственных функций по методу Келлога
- •§13. Сопряжённые однородные интегральные уравнения
- •§23. Перед тем, как перейти к исследованию неоднородного интегрального уравнения при , рассмотрим однородное интегральное уравнение
- •§15. Теорема Адамара
- •§16. Обзор других методов решения. Приближённые методы решения
- •§16. Задачи для самостоятельного решения
- •Примерный вариант тест-контрольной работы
- •Литература
- •Оглавление
- •Тест-контрольная по интегральным уравнениям Вольтерра
- •1 Вариант
- •9.Записать решение уравнения, если резольвента ядра известна
- •Вариант
- •Вариант
- •Вариант
- •Вариант теста по интегральным уравнениям Вольтерра
- •Ответы к тестам по интегральным уравнениям Вольтерра
- •Блок1. Интегральные уравнения Вольтерра
§4. Решение интегральных уравнений Фредгольма с помощью ряда Неймана
Рассмотрим уравнение второго рода
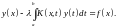 (4.1)
(4.1)
Решение будем искать в виде ряда по степеням параметра
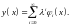 (4.2)
(4.2)
Подставив ряд (4.2) в уравнение (4.1)

и приравнивая коэффициенты при одинаковых степенях слева и справа в полученном равенстве (так как ряды слева и справа от равенства равны только в этом случае) найдем
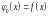 ,
,
 ,
,
 ,
,
……………………………………………………………………………
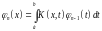 .
.
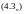
Докажем
сходимость ряда (4.2) при
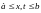 и следующих ограничениях
и следующих ограничениях
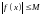 ,
,
 ,
,
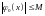 .
(4.4)
.
(4.4)
Для выполнения условий (4.4) достаточно чтобы функция f(x) и ядро K(x,t) в рассматриваемой области были непрерывными. Для ядра K(x,t) можно условие ослабить, потребовав только его регулярность.
Оценим коэффициенты ряда (4.2) по модулю в этой области
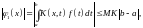
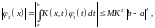
……………………………………………………………………………
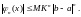
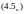
……………………………………………………………………………………………………………….
Выпишем ряд для искомой функции
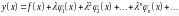
и ряд составленный из полученных оценок (4.5n)
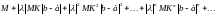 ,
(4.6)
,
(4.6)
который сходится по признаку Даламбера
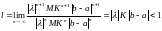 ,
если
,
если
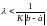 или
или
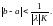 (4.7)
(4.7)
Ряд (4.6) по построению является мажорирующим для ряда (4.2), следовательно ряд (4.2) по критерию Вейерштрасса сходится равномерно и абсолютно при выполнении условий (4.7). Полученная функция в виде ряда (4.2) является решением уравнения (4.1).
Пример 3. Решить интегральное уравнение методом разложения по параметру
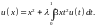
Решение. Подставим ряд по степеням параметра
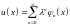 ,
,
в заданное уравнение
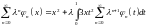
и, приравнивая коэффициенты при одинаковых степенях найдём
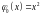 ,
,
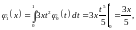
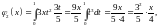
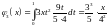 ,
… ,
,
… ,
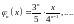


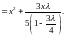 ;
;
Ответ:
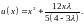
Ответ
получен для
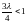 ;
;
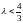 ,
но нетрудно проверить, что полученное
решение удовлетворяют уравнению при
всех значениях
,
кроме
,
но нетрудно проверить, что полученное
решение удовлетворяют уравнению при
всех значениях
,
кроме
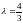 .
.
§5. Итерированные ядра и резольвента интегральных уравнений Фредгольма
В
полученных выражениях
коэффициентов ряда Неймана
 последовательно произведем подстановку
последовательно произведем подстановку
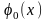 в
в
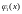 ,
затем
,
затем
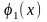 в
в
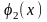 и так далее, сменив в процессе преобразований
обозначения переменных
и так далее, сменив в процессе преобразований
обозначения переменных
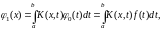
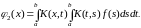
В кратных интегралах изменим порядок интегрирования в соответствии с ниже изображенной областью интегрирования в уравнении типа Фредгольма

b



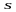
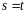
а
0
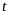
b
а

Введем понятие итерированных ядер, положив

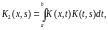
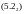
тогда
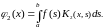
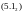
Аналогично найдём
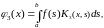
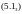
где
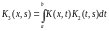 ,
,
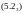
……………………………………………………………………………
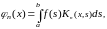
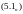
где

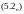 ……………………………………………………………………………
……………………………………………………………………………
Подставим
выражения коэффициентов
,
в соответствии с полученными формулами
в ряд (4.2) и, в силу равномерной и
абсолютной сходимости этого ряда, можем
просуммировать интегралы

Выражение в квадратных скобках назовем резольвентой интегрального уравнения Фредгольма второго рода и для нее введем обозначение
 .
(5.3)
.
(5.3)
Если итерированные ядра найдены, а следовательно и резольвента, то решение интегрального уравнения Фредгольма (4.1) определится по формуле
 (5.4)
(5.4)
Аналогично, группируя интегралы попарно в формулах

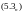
для
коэффициентов
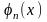 начиная с последней пары, для итерированных
ядер получим другую формулу
начиная с последней пары, для итерированных
ядер получим другую формулу
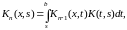 n=2,3,…
n=2,3,…

В формулу резольвенты (5.3) подставив выражения итерированных ядер или получим формулу для решения интегральных уравнений Фредгольма второго рода
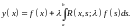 (5.6)
(5.6)
Из формулы резольвенты (5.3), заменив выражения итерированных ядер по формулам и группируя интегралы, получим интегральное уравнение резольвенты
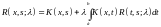 ,
(5.7)
,
(5.7)
которое называют первым фундаментальным соотношением Фредгольма.
Аналогично можно получить другое уравнение резольвенты если воспользоваться формулами
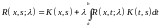 ,
(5.8)
,
(5.8)
которое соответственно называют вторым фундаментальным соотношением Фредгольма.
Для итерированных ядер справедливо также соотношение
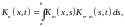 (5.9)
(5.9)
где
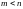 ,
которое получим, если начать попарно
менять порядок интегрирования одновременно
слева и справа с некоторого m.
,
которое получим, если начать попарно
менять порядок интегрирования одновременно
слева и справа с некоторого m.
Пример 3. Найти резольвенту и записать решение уравнения
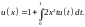
Найдём
итерированные ядра по формулам
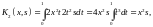
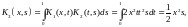
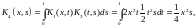
……………………………………………………..
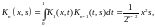 ……………………………………………………..
……………………………………………………..
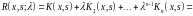
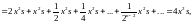
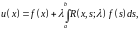
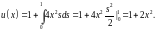
Сделаем проверку