22. Основные свойства спектральной плотности.

Отметим, что в формулах и ,S_uu(w) определима как для положительных, так и для отрицательных частот. Перейдем к одностороннему спектру, ограничиваясь только положительными частотами. Воспользовавшись формулой Эйлера, представим соотношение 2, состоящим из двух слагаемых

В силу частности функции R_u(t) второе слагаемое равно нулю, а первое можно преобразовать к виду

(105)-следует, что S_uu(w) является действительной и четной функцией, т.е.S_uu(w) = S_uu(-w) (106)

Это позволяет ограничиться положительными частотами и в (1): (107)

Соотношения (1) и (2), а также (105) и (107) являются парами интегрального преобразования Фурье, причем (105) и (107) для случая четной функции. Поэтому корреляционная функция и спектральная плотность подчинены закономерности: чем протяженнее кривая S_uu(w), тем уже корреляционная функция R_u(t) (тем меньше время корреляции) и наоборот.

Площадь ограниченная непрерывной кривой S_uu(w) по спектр-й диаграмме, очевидно должна равняться дисперсии D_u случайного процесса U(t). В(107)приt = 0, получим

(108)

Подразумевая под случайным процессом U(t) напряжение, D_u можно рассматривать как среднюю мощность, выделяемую этим напряжением на резисторе с сопротивлением в 1 Ом:

(109)следовательно, величина (110)

представляет собой долю средней мощности, выделяемой составляющими спектра, относящимися к интервалу частот (w,w + dw).

В связи с этим спектральную плотность S_uu(w) называют еще спектральной плотностью мощности, а также энергетическим спектром стационарного случайного процесса, поскольку S_uu(w) имеет размерность энергии.

Спектральная плотность мощности случайного процесса является средней характеристикой множества реализаций. Ее можно получить и путем усреднения спектральной плотности мощности реализации P_k(w) (62) по множеству реализаций.

Рассмотрим с этой целью одну реализацию стационарного случайного процесса U(t) сначала на ограниченном интервале времени –Т<t<T. Для нее можно записать преобразование Фурье:

(111)

В соответствии с (63) спектральная плотность мощности этой реализации

(112)

Найдем среднее значение по множеству реализаций k. Имеем

или (113)

Т.к. мы предполагаем, что случайный процесс стационарный, то (114) где t₁ – t₂ = t.

При выполнении условия (114) для выражения (113) существует предел при Т®¥:

(115)ч т д

23. Дискретизация непрерывных величин.

. По своей природе все физические величины являются непрерывными. Передача информации о непрерывной величине может осуществляться, например, по структурной схеме, приведенной на рисунке. Величина Х подается на вход преобразователя 1, на выходе которого получается также электрическая непрерывная величинаY, (ток, напряжение, частота), причем Y = F (X).

Рис. 1. Схема передачи информации о непрерывной величине.

Величина Y поступает в канал связи 2, на приемном конце которого включен электроизмерительный прибор со шкалой, градуированной в единицах величины Х. Схема эта проста и широко применяется. Недостатки этого способа:

• сильное влияние помех, искажающих результат;

• сложность обработки аналоговой информации;

• сложность передачи информации на большие расстояния.

Поэтому передача измерительной информации о непрерывных величинах в настоящее время производится с применением дискретизации передаваемой величины.

На рис. 2 дан график, поясняющий идею дискретизации. Если имеется непрерывная величина Y = f(t), то диапазон возможных значений ее можно разбить на «n» уровней с шагом y и в дальнейшем при передаче сведений, например в момент времени t₁, сообщать не действительное значение величины, равное y=f(x), а дискретное рациональное число y_kв = k_iy, соответствующее ближайшему уровню квантования k_i.

При этом передача сведений будет происходить с неизбежными погрешностями. Погрешность квантования явл случайной величиной. Можно показать, что закон ее распределения будет равномерным с диапазоном возможных значений от –0,5y до +0,5y. Плотность вероятности погрешности квантования в указанных пределах будет

при среднем квадратичном отклонении

Уменьшая шаг квантования, можно получить желаемую точность сведений.

23. Квантование по времени и теорема Котельникова.

При равномерном квантовании по времени руководствуются теоремой В.А.Котельникова, указывающей при каких условиях непрерывная функция времени может быть восстановлена идеально точно по значениям ее дискретных ординат.

Т:Если непрерывная функция времени f(t) не содержит составляющих с частотой выше F_max, то она вполне определяется дискретными значениями, отсчитываемыми через интервалы времени

Доказательство этой теоремы основывается на возможности представления функции f(t), имеющей ограниченный спектр, в виде ряда (1)

Функция (2) Здесь k- целые числа, как положительные, так и отрицательные; t – время; t – постоянная величина, равная 1/F_max.

Не рассматривая мат доказательства такого разложения, приведем только его геометрическую интерпретацию графиком, показанным на рис. 3.

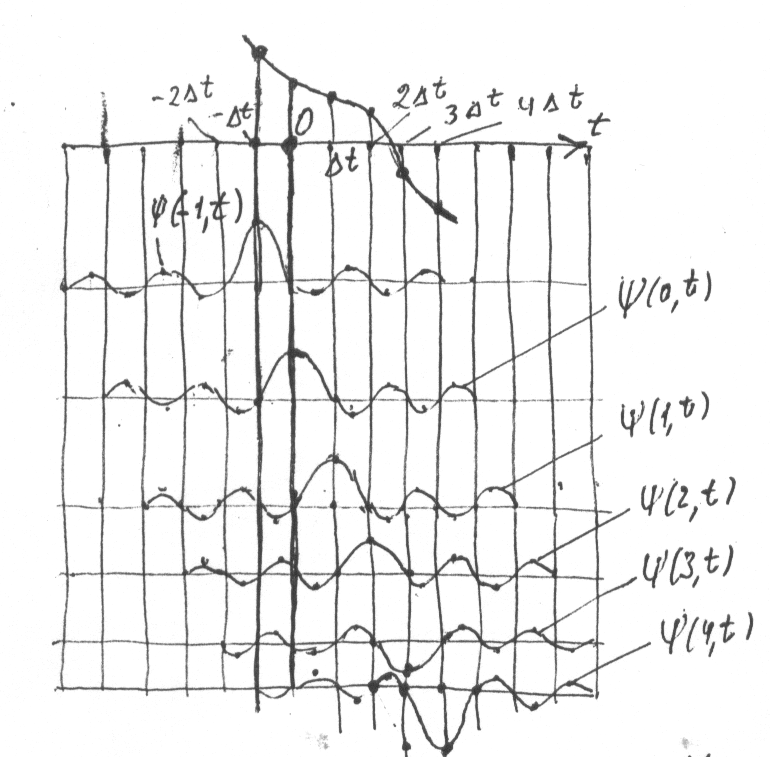
Рис. 3. Разложение функции f(t) в ряд составляющих (k,t), где k – целое число

Из рис видно, что к-е из слагаемых является ф-ей времени с убывающей ампл-й. Если в (2) индексу k придать некоторое значение l, то в момент t_l=lt функция (kt) становится неопределенностью вида 0/0, т.к. множитель (t-lt) в знаменателе равен нулю и числитель тоже будет равен нулю. Для раскрытия неопределенности берем отношение производных:

Учитывая (2), получаем

т.е. каждое слагаемое с любым номером l в момент времени t=lt становится равным f(t).

В тот же момент времени все остальные слагаемые с номером ml будут иметь множитель Но и, следовательно, , т.к. l и m – целые числа, т.е. все слагаемые в момент времени t=lt становятся равными нулю, кроме слагаемого с номером l, которое в этот момент равно f(t).

Т обр, на основе Т Котельникова делают вывод, что для информации о непрерывной величине достаточно передавать ее значение через интервалы времени

, (3)где F_max – частота наивысшей гармонической составляющей.