18. Стационарные и эргодические случайные процессы.

Случайный процесс называют стационарным в узком смысле, если выражения для плотностей вероятности не зависят от начала отсчета времени

(78)

где - случайная величина, отражающая значение процесса в момент времени t = t_i +  (- произвольное число).

Процесс U(t) принято называть стационарным в широком смысле, если выполняется условие постоянства математического ожидания и дисперсии, а, корреляционная функция не зависит от начала отсчета времени и является функцией только одного аргумента  = t₂ - t_1,т.е.

(79)

(80)

(81)

Т.к. условие постоянства дисперсии является частным случаем требования к корреляционной функции при  = 0:

то выполнение соотношений (79) и (81) достаточно, чтобы рассматривать случайный процесс U(t) как стационарный.

Случайные процессы, наблюдаемые в устойчиво работающих реальных системах, имеют конечное время корреляции. Поэтому для стационарных процессов, представляющих практический интерес, справедливо соотношение

(82)

Если для случайного процесса равенства (79), (81) не выдерживаются, но на интересующем нас интервале времени изменением указанных параметров можно пренебречь, его называют квазистационарным.

Среди стационарных случайных процессов многие удовлетворяют свойству эргодичности. Оно проявляется в том, что каждая реализация случайного процесса достаточной продолжительности несет практически полную информацию о свойствах всего ансамбля реализаций, поэтому заменяют усреднение значений по ансамблю реализаций усреднением значений одной реализации за длительный интервал времени.

Следовательно, для стационарных эргодических процессов справедливы соотношения

(83)

(84)

(85)

где u(t) – конкретная реализация случайного процесса U(t).

Для облегчения практического определения корреляционной функции в соответствии с (85) серийно выпускаются специальные вычислительные устройства – коррелометры (корреляторы).

19.Спектральное представление случайных сигналов.

Рассмотрим случайный процесс U(t), имеющий математическое ожидание m_u(t). Соответствующий центрированный случайный процесс характеризуется в момент времени t₁ центрированной случайной величиной :

(86)

Центрированный случайный процесс можно выразить в виде конечной или бесконечной суммы ортогональных составляющих, каждая из которых представляет собой неслучайную базисную функцию _k(t) с коэффициентом C_k, являющимся случайной величиной. Имеем разложение центрированного случайного процесса :

(87)

Случ величины C_k наз-ся коэффициентами разложения. В общ случ они статистически зависимы, эта связь задается матрицей коэффициентов корреляции ||R_ki||. Мат ожидания коэфф-в разложения =нулю. Неслучайные базисные функции наз-т координатными функциями.

Для конкретной реализации коэффициенты разложения являются действительными величинами и определяются:

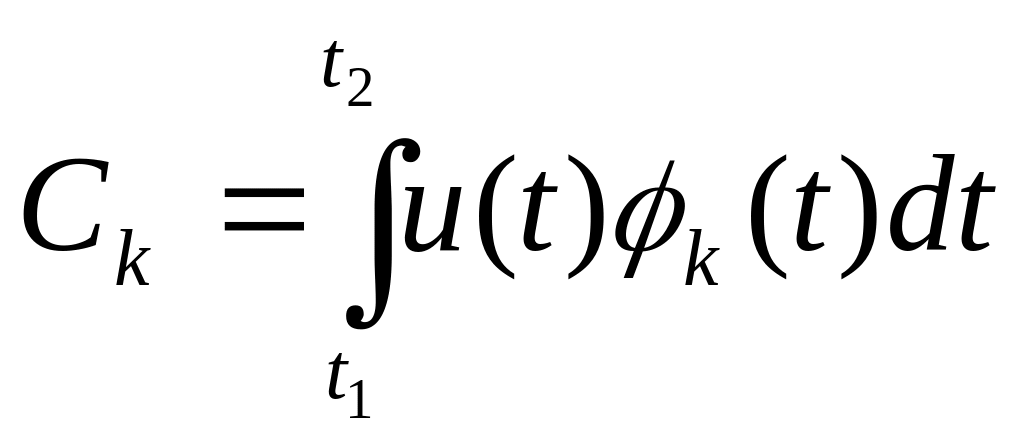([7])

Предположив, что , детерминированную функцию m_u(t) в (86) на интервале –T<t<T также можно разложить по функциям _k(t), представив в виде

, (87а)

. (87б)

Подставляя (87), (87а) в (86) для случайного процесса U(t) с отличным от нуля средним, получим

. (87в)

Выражение случайного процесса в виде (87в) позволяет существенно упростить его линейные преобразования, т.к.они сводятся к преобразованиям детерминированных функций [m_u(t), ], а коэффициенты разложения, являющиеся случайными величинами, остаются неизменными.

Чтобы определить требования к координатным функциям, рассмотрим корреляционную функцию процесса , заданную разложением

.

Так как D_k – дисперсия коэффициента C_k

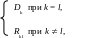
то

(88)

(88) проще, если коэффициенты {C_k} некоррелированы (R_kl=0 при kl, R_kl=D_k при k=l):

. (89)

В частности, при t₁ = t₂ = t получим дисперсию случайного процесса U(t)

(90)

Поэтому целесообразно выбирать такие координатные функции, которые обеспечивают некоррелированность случайных величин {C_k}. Разложение (87), удовлетворяющее этому условию, называют каноническим разложением.

при выбранном наборе координатных функций центрированный случайный процесс характеризуется совокупностью дисперсий коэффициентов разложения, которую можно рассматривать как обобщенный спектр случайного процесса.