
- •Введение.
- •Глава 1. Термодинамика.
- •§ 1. Исходные понятия и постулаты тд.
- •§ 2. I начало тд. Теплоемкости.
- •I начало тд обобщает закон сохранения энергии для тд процессов: количество теплоты, сообщаемое системе, идет на изменение ее внутренней энергии и совершение системой работы.
- •§ 3. Применение I начала тд к равновесным процессам в идеальных газах.
- •§ 4. Обратимые процессы. Циклические процессы. Цикл Карно. Теоремы Карно.
- •§ 5. Второе начало тд.
- •§ 6. Энтропия. Свободная энергия. Энтальпия.
- •I.) Энтропия.
- •II.) Энтальпия.
- •III.) Свободная энергия.
- •§ 7. III начало тд.
- •§ 8. Термодинамические потенциалы. Метод термодинамических потенциалов.
- •§ 9. Условия равновесия и устойчивости систем.
- •7. Условие равновесия изолированной двухфазной однокомпонентной системы.
§ 3. Применение I начала тд к равновесным процессам в идеальных газах.
Опытным путем, еще до появления молекулярно-кинетической теории, был установлен целый ряд законов, описывающих поведение идеальных газов в различных процессах. Эти законы можно назвать уравнениями процессов. Обобщив эти уравнения, французский физик Б. Клапейрон вывел уравнение состояния идеального газа, а Д.И. Менделеев ввел универсальную газовую постоянную, поэтому уравнение состояния идеального газа называется уравнением Менделеева-Клапейрона.
Запишем
первое начало термодинамики для одного
моля идеального газа,
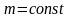 .
.
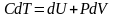
Изохорический процесс - процесс, происходящий при постоянном объеме.
Для
изохорического процесса давление и
температура связаны между собой законом
Гей-Люссака
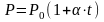 ,
где
,
где
 - термический коэффициент изменения
давления,
- термический коэффициент изменения
давления,
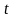 - температура в градусах Цельсия.
- температура в градусах Цельсия.
Э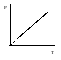 то
уравнение на диаграмме состояний в
то
уравнение на диаграмме состояний в
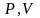 -координатах
представляет собой прямую параллельную
оси
,
а на диаграмме в
-координатах
представляет собой прямую параллельную
оси
,
а на диаграмме в
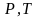 -координатах
представляет собой прямую, как бы
выходящую из начала координат, если
температуру по оси
,
будем откладывать в Кельвинах. Если
температуру будем откладывать в Цельсиях,
то изохора пересечет ось
-координатах
представляет собой прямую, как бы
выходящую из начала координат, если
температуру по оси
,
будем откладывать в Кельвинах. Если
температуру будем откладывать в Цельсиях,
то изохора пересечет ось
 температур в точке
температур в точке
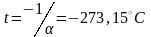 .
Отсюда
.
Отсюда
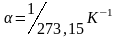 .
.
Закон
Гей-Люссака имеет и более удобный вид:
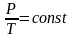 .
.
П ри
изменении состояния идеального газа
с
ри
изменении состояния идеального газа
с
 на состояние
на состояние
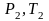 согласно закону Гей-Люссака получим
уравнение процесса
согласно закону Гей-Люссака получим
уравнение процесса
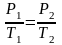 ,
связывающее параметры начального и
конечного состояния идеального газа.
,
связывающее параметры начального и
конечного состояния идеального газа.
Для
этого процесса
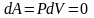 .
Система не совершает работу,
следовательно, количество теплоты,
передаваемое системе, идет на изменение
ее внутренней энергии
.
Система не совершает работу,
следовательно, количество теплоты,
передаваемое системе, идет на изменение
ее внутренней энергии
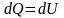 .
.
Таким
образом, I начало ТД для изохорического
процесса:
количество
теплоты, передаваемое системе, идет на
изменение внутренней энергии системы.
С учетом теплоемкости выглядит так:
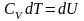 .
.
Изменение
внутренней энергии одного моля идеального
газа, с учетом молярной теплоемкости
и калорического уравнения состояния
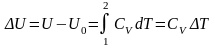 .
.
Для
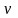 молей вещества
молей вещества
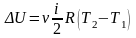 .
.
Изобарический процесс - процесс, происходящий при постоянном давлении.
Для
изобарического процесса объем и
температура связаны между собой законом
Гей-Люссака
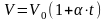 ,
где
- термический коэффициент объемного
расширения,
- температура в градусах Цельсия.
,
где
- термический коэффициент объемного
расширения,
- температура в градусах Цельсия.
Э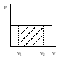 то
уравнение на диаграмме состояний в
-координатах
представляет собой прямую параллельную
оси
,
а на диаграмме в
то
уравнение на диаграмме состояний в
-координатах
представляет собой прямую параллельную
оси
,
а на диаграмме в
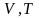 -координатах
представляет собой прямую, как бы
выходящую из начала координат. В общем
случае при
-координатах
представляет собой прямую, как бы
выходящую из начала координат. В общем
случае при
 закон не выполняется, т.к. газы переходит
в жидкое состояние (за исключением
гелия). Если температуру будем откладывать
в Цельсиях, то изохора как бы пересечет
ось
температур в точке
.
Аналогично уравнению изохорического
процесса, закон Гей-Люссака имеет и
другой более удобный вид:
закон не выполняется, т.к. газы переходит
в жидкое состояние (за исключением
гелия). Если температуру будем откладывать
в Цельсиях, то изохора как бы пересечет
ось
температур в точке
.
Аналогично уравнению изохорического
процесса, закон Гей-Люссака имеет и
другой более удобный вид: 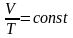 .
.
П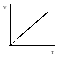 ри
изменении состояния идеального газа
с
ри
изменении состояния идеального газа
с
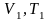 на состояние
на состояние
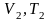 согласно закону Гей-Люссака получим
уравнение процесса
согласно закону Гей-Люссака получим
уравнение процесса
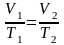 ,
связывающее параметры начального и
конечного состояния идеального газа.
,
связывающее параметры начального и
конечного состояния идеального газа.
Для
этого процесса
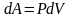 .
Система совершает работу при расширении
от объема
.
Система совершает работу при расширении
от объема
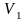 до объема
до объема
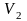 ,
температура системы соответственно
изменяется от
,
температура системы соответственно
изменяется от
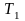 до
до
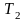 графически эту работу можно представить,
как площадь под графиком процесса в
-координатах.
Вычислим интеграл и получим выражение
для работы:
графически эту работу можно представить,
как площадь под графиком процесса в
-координатах.
Вычислим интеграл и получим выражение
для работы:
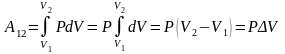
 .
.
Выразим
работу через изменение температуры.
Запишем систему из уравнений состояния
моля идеального газа и:
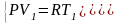 ,
отнимем от второго уравнения первое
,
отнимем от второго уравнения первое
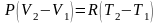 ,
отсюда получим
,
отсюда получим
 .
.
Для
молей вещества:
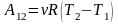
Изменение
внутренней энергии в этом процессе
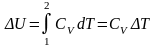 .
.
Для молей вещества .
I начало ТД для изобарического процесса: количество теплоты, передаваемое системе, идет на изменение ее внутренней энергии и совершение системой работы. В дифференциальной форме для одного моля с учетом теплоемкости:
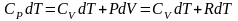 .
.
Изотермический процесс - процесс, происходящий при постоянной температуре.
Изотермический процесс можно осуществить, поместив систему, сосуд с поршнем, в термостат. Термостат – тело с настолько большой теплоемкостью , что его температура при теплообмене с какой-либо системой не меняется. Когда говорят о системе помещенной в термостат, то имеют в виду систему, в которой при всех происходящих в ней процессах (расширение, намагничивание и т.д.) температура поддерживается постоянной.
Если в этих условиях перемещать поршень вниз, то под действием внешней силы газ будет сжиматься, и работу будет совершать внешняя сила. Если газ будет расширяться, то поршень будет перемещаться вверх, и работу будет совершать газ.
Для
реализации условий
 изменения
должна происходить
- медленно.
изменения
должна происходить
- медленно.
У равнение
изотермического процесса – это уравнение
Бойля-Мариотта.
равнение
изотермического процесса – это уравнение
Бойля-Мариотта.
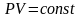
Уравнение
изотермы на диаграмме состояний в
-координатах
представляет собой гиперболу, положение
которой зависит от
.
Если газ переходит из состояния
 в состояние
в состояние
 ,
то уравнение состояния выглядит так
,
то уравнение состояния выглядит так
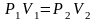 или
или
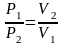 .
.
Система
совершает работу при расширении от
объема
до объема
,
давление в системе соответственно
изменяется от
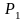 до
до
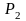 ,
графически эту работу можно представить,
как площадь под графиком изотермы в
-координатах.
Вычислим интеграл и получим выражение
для работы одного моля газа:
,
графически эту работу можно представить,
как площадь под графиком изотермы в
-координатах.
Вычислим интеграл и получим выражение
для работы одного моля газа:
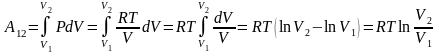
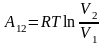 .
.
При
вычислении учли, что давление и объем
связаны уравнением состояния
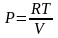 ,
если учтем уравнение процесса, то получим
другое выражение
,
если учтем уравнение процесса, то получим
другое выражение
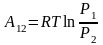 .
.
Для
молей идеального газа
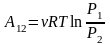
Для
изотермического процесса

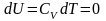 изменение внутренней энергии равно
нулю.
изменение внутренней энергии равно
нулю.
I
начало ТД для изотермического процесса:
в
изотермическом процессе все количество
теплоты, передаваемое системе, идет на
совершение системой работы по расширению.
В дифференциальной форме для одного
моля:
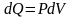 .
.
Адиабатический процесс - процесс, происходящий в изолированной системе, когда нет теплообмена с окружающей средой.
Для
адиабатического процесса
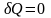 и I
начало ТД в дифференциальной форме
и I
начало ТД в дифференциальной форме
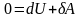 .
С учетом зависимости внутренней энергии
от температуры:
.
С учетом зависимости внутренней энергии
от температуры:
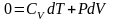
I
начало ТД для адиабатического процесса:
в адиабатическом процессе система
совершает работу за счет убыли внутренней
энергии
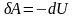 ,
и наоборот, работа, совершаемая над
системой идет на увеличение ее внутренней
энергии
,
и наоборот, работа, совершаемая над
системой идет на увеличение ее внутренней
энергии
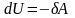 .
.
Получим из I начала ТД и уравнения состояния идеального газа уравнение адиабатического процесса (уравнение адиабаты).
Продифференцируем уравнение состояния для одного моля идеального газа .
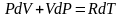
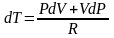 ,
подставим в I
начало ТД
,
подставим в I
начало ТД
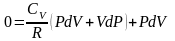 ,
перегруппируем подобные слагаемые,
,
перегруппируем подобные слагаемые,
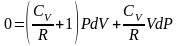 приведем
выражение в скобке к общему знаменателю
приведем
выражение в скобке к общему знаменателю
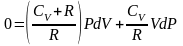 учтем
соотношение Майера
учтем
соотношение Майера
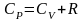 и разделим на
и разделим на
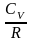
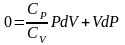 ,
введем обозначение отношения
,
введем обозначение отношения
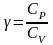 ,
оно называется - показатель адиабаты.
Разделим переменные и решим дифференциальное
уравнение, взяв интеграл:
,
оно называется - показатель адиабаты.
Разделим переменные и решим дифференциальное
уравнение, взяв интеграл:
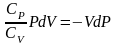
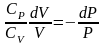
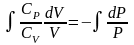
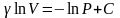 отсюда
отсюда
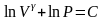
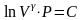
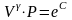 .
.
Уравнение
адиабаты
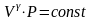 ,
было получено Пуассоном, и
,
было получено Пуассоном, и
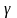 еще называют коэффициентом Пуассона.
Учитывая уравнение состояния, для
уравнения адиабаты есть и другие способы
записи:
еще называют коэффициентом Пуассона.
Учитывая уравнение состояния, для
уравнения адиабаты есть и другие способы
записи:
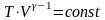 ,
,
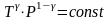 .
.
Уравнения
Пуассона применимы только для описания
квазистатических адиабатических
процессов, уравнения справедливы лишь
в интервале давлений, где величина
постоянная. Т.к.
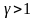 ,
то при адиабатическом сжатии газ
нагревается, а при адиабатическом
расширении – охлаждается.
,
то при адиабатическом сжатии газ
нагревается, а при адиабатическом
расширении – охлаждается.
В
общем случае нужно учитывать, что
функция
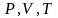 ,
т.е.
,
т.е.
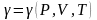 .
.
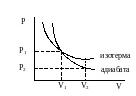
Уравнение адиабаты на диаграмме состояний в -координатах представляет собой гиперболу, положение которой зависит от , но график идет круче чем изотерма для той же системы, т.к. при увеличении объема давление уменьшается быстрее. Если газ переходит из состояния в состояние , то площадь под графиком изотермы больше, чем площадь под графиком адиабаты и, следовательно, система изотермическом процессе совершает большую работу, чем в адиабатическом процессе при том же расширении.
Вычислим работу, совершаемую идеальным газом в адиабатическом процессе расширения от объема до объема :
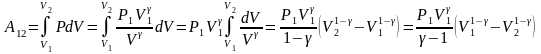 ,
если вынести из скобок
,
если вынести из скобок
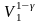 ,
учесть
,
учесть
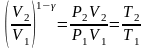 то получим более простые выражения
то получим более простые выражения
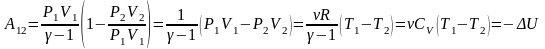 .
.
Каждое выражение можно использовать для вычисления численного значения произведенной работы в конкретном процессе.
Таким
образом, работа при одном и том же
изменении объема в адиабатическом
процессе меньше, чем в изотермическом
процессе. Но она существенно зависит
от показателя адиабаты
.
При значении
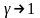 величина работы стремится к значению
при изотермическом процессе.
величина работы стремится к значению
при изотермическом процессе.
Политропный процесс - процесс, при котором теплоемкость системы остается постоянной
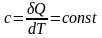 .
При таком процессе происходит частичный
теплообмен системы с окружающей средой.
.
При таком процессе происходит частичный
теплообмен системы с окружающей средой.
Это самый общий процесс, т.к. полностью исключить теплообмен системы с окружающей средой практически невозможно.
I начало ТД для политропного процесса: количество теплоты, передаваемое системе, идет на изменение ее внутренней энергии и совершение системой работы. В дифференциальной форме для одного моля с учетом теплоемкости:
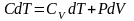
Получим из I начала ТД и уравнения состояния идеального газа уравнение политропного процесса (уравнение политропы)
Продифференцируем уравнение состояния для одного моля идеального газа .
, подставим в I начало ТД
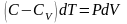
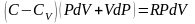 ,
перегруппируем подобные слагаемые,
,
перегруппируем подобные слагаемые,
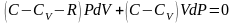
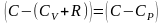 учтем
соотношение Майера
учтем
соотношение Майера
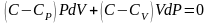 разделим
на
разделим
на
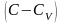
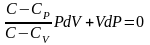 ,
введем обозначение отношения
,
введем обозначение отношения
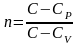 ,
оно называется - показатель политропы.
,
оно называется - показатель политропы.
Разделим переменные и решим дифференциальное уравнение, взяв интеграл:
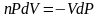
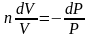
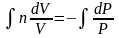
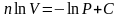 отсюда
отсюда
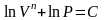
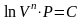
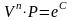 .
.
Уравнение
политропы
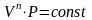 .
.
Учитывая уравнение состояния, для уравнения политропы, аналогично уравнению адиабаты, есть и другие способы записи:
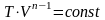
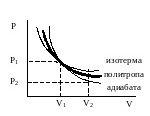 ,
,
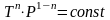 .
.
График политропы на диаграмме состояний в - координатах представляет собой гиперболу, занимающую промежуточное положение между изотермой и адиабатой.
Работа, совершаемая в политропном процессе, вычисляется аналогично работе в изобарическом процессе:
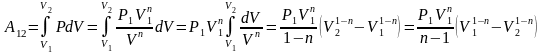
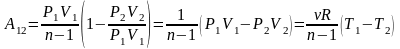 .
.
Если
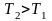 ,
то
,
то
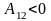 работа совершается над газом, газ
сжимается.
работа совершается над газом, газ
сжимается.
Изменение внутренней энергии в этом процессе , как и для всех других процессов в идеальном газе.
Для молей вещества .
Числовые
значения показателя политропы
 определяются опытным путем.
определяются опытным путем.
З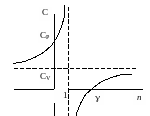 ависимость
теплоемкости
ависимость
теплоемкости
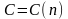 от
для идеального газа показана на графике.
от
для идеального газа показана на графике.
Все изопроцессы могут быть рассмотрены, как предельные случаи политропного процесса.
адиабатический процесс .
В
этом процессе
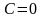 ,
показатель политропы превращается в
показатель адиабаты
,
показатель политропы превращается в
показатель адиабаты
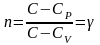 .
.
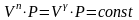 уравнение
политропы превращается в уравнение
адиабаты.
,
,
.
уравнение
политропы превращается в уравнение
адиабаты.
,
,
.
изотермический процесс .
В
этом процессе
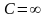 ,
показатель политропы равен единице
,
показатель политропы равен единице
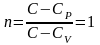 .
.
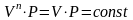 уравнение
политропы превращается в уравнение
изотермы.
уравнение
политропы превращается в уравнение
изотермы.
, , .
изобарический процесс .
В
этом процессе
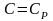 ,
показатель политропы равен нулю
,
показатель политропы равен нулю
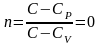 .
.
 ,
уравнение политропы превращается в
уравнение изобары.
,
уравнение политропы превращается в
уравнение изобары.
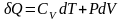 ,
,
,
,
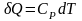 ,
,
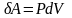 .
.
изохорический процесс .
В
этом процессе
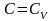 ,
показатель политропы равен бесконечности
,
показатель политропы равен бесконечности
 .
.
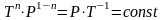 ,
уравнение политропы превращается в
уравнение изохоры.
,
уравнение политропы превращается в
уравнение изохоры.
,
 ,
.
,
.
