
- •1.Кільце многочленів к[X].
- •Означення многочлена
- •Дії над многочленами.
- •Подільність в кільці многочленів p[X],де р-поле. План
- •Спосіб знаходження нсд двох многочленів – алгоритм Євкліда.
- •Лінійне представлення нсд
- •Корені многочлена План
- •Означення і ознака кореня многочлена. Кратні корені.
- •3. Формули Вієта.
Корені многочлена План
Означення і ознака кореня многочлена. Кратні корені.
Теорема про найбільшу можливу кількість коренів многочлена.
Існування кореня многочлена над довільним полем. Формули Вієта.
Про алгебраїчну і функціональну рівність многочленів. Приклади.
Означення і ознака кореня многочлена. Кратні корені.
Означення 1: Коренем многочлена f(x)є P[x] називається елемент α поля Р такий, що f(α)=0.
Корінь многочлена f(x) називають також нулем многочлена f(x).
Теорема1: Елемент α є Р є коренем многочлена f(x)є P[x] тоді і тільки тоді, коли лінійний двочлен х- α є дільником многочлена с
Доведення:
За
т. Безу остача від ділення f(x)
на х- α дорівнює f(α).
Отже, f(x)![]() х- α тоді і тільки тоді, коли f(α)=0,
тобто α – корінь многочлена f(x).
х- α тоді і тільки тоді, коли f(α)=0,
тобто α – корінь многочлена f(x).
Ця ознака – необхідна і достатня умова того, щоб α – був коренем многочлена.
Означення 2: Елемент α є Р називається коренем многочлена f(x)є P[x], якщо f(x) ділиться на х-α .
Означення
3:
Елемент α є Р називається
k-кратним
коренем (або коренем k-ї
кратності) многочлена f(x)є
P[x],
якщо f(x)
ділиться на (х ![]() але не ділиться
на
але не ділиться
на ![]() .
.
Отже,
кратність кореня α многочлена f(x)
є найбільше з натуральних чисел m
таких,
що ![]() є
дільником f(x)
у кільці P[x].
є
дільником f(x)
у кільці P[x].
Корені кратності 1 називаються простими, корені кратності 2 і більше- кратними, двократні і трикратні корені іноді називають подвійними та потрійними.
Якщо
f(x)-нуль-многочлен,
то будь-який елемент α є Р є його коренем,
причому кратність цього кореня не можна
визначити, бо нуль-многочлен ділиться
на ![]() при довільному натуральному m.
α є Р k-кратним
коренем многочлена, f(x)є
P[x]
тоді і тільки тоді , коли f(x)=g(x),
(1) де g(x)-многочлен
над полем Р для якого α не є коренем.
при довільному натуральному m.
α є Р k-кратним
коренем многочлена, f(x)є
P[x]
тоді і тільки тоді , коли f(x)=g(x),
(1) де g(x)-многочлен
над полем Р для якого α не є коренем.
Приклад 1:
f(x)=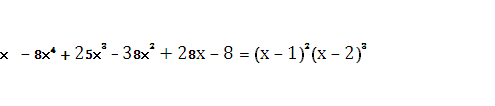
«1» - подвійний , «2» - потрійний корінь многочлена.
Приклад 2:
Многочлен
f(x)= над полем
Q
має
n-кратний
корінь α=0.
над полем
Q
має
n-кратний
корінь α=0.
Теорема (про найбільшу можливу кількість коренів многочлена).
Нехай
f(x)є
P[x],
![]() є
Р є коренем , f(x)
кратності
є
Р є коренем , f(x)
кратності ![]() ,
,
![]() є
є![]() -коренем
f(x)
кратності
-коренем
f(x)
кратності ![]() …,
…,![]() є
Р- коренем f(x)
кратності
є
Р- коренем f(x)
кратності ![]() ,
причому
,
причому ![]() при і
при і![]() .
Тоді, згідно з (1) можна записати
.
Тоді, згідно з (1) можна записати
f(x)=![]() (2)
(2)
де
![]() не ділиться на
не ділиться на ![]() .
.
Оскільки
f(x)
має ділитись на ![]() (але
не на (
(але
не на (![]() ),
а
),
а ![]() взаємно простий з
то з (2) видно, що
ділиться
на
(але не на (
взаємно простий з
то з (2) видно, що
ділиться
на
(але не на (![]() ), тобто
), тобто
f(x)=![]()
![]() ,
де
- многочлен, який не має своїми коренями
,
де
- многочлен, який не має своїми коренями
![]() і
.
і
.
Продовжуючи міркувати в такий же спосіб (тобто, по суті, застосовуючи метод математичної індукції ),дістанемо :
f(x)=
…![]() ,
(3)
,
(3)
де
![]() - многочлен, для якого жодний ж елементів
- многочлен, для якого жодний ж елементів
![]() не є коренем. З (3) видно, що deg
f
=
+
не є коренем. З (3) видно, що deg
f
=
+![]() …+
…+![]() deg
m
, тобто
deg
m
, тобто
+ …+ = n
Отже, число коренів многочлена f(x) у полі Р не може перевищувати степеня цього многочлена, коли навіть кожний корінь ураховували стільки разів, яка кратність.
Теорема 2: Число усіх можливих коренів многочлена f(x) над полем Р не перевищує його степеня.
3.Існування кореня многочлена над довільним полем. Формули Вієта.
Наведемо приклади многочленів над полем Р, які не мають жодного корення у цьому полі.
![]() над полем
Q не має рац. коренів. Многочлен
над полем
Q не має рац. коренів. Многочлен ![]() над
полем R
не має дійсних коренів. Але кожній з цих
многочленів має корені в деякому
розширенні розглядуваного поля, а саме:
над
полем R
не має дійсних коренів. Але кожній з цих
многочленів має корені в деякому
розширенні розглядуваного поля, а саме:
![]() має корені
має корені ![]()
![]() корені
корені ![]() .
.
Теорема
3 (Кронекера):
Якщо ![]() довільний многочлен над полем Р, для
якого
довільний многочлен над полем Р, для
якого ![]() то існує
розширення К поля Р, в якому є корінь
.
то існує
розширення К поля Р, в якому є корінь
.
Теорема
4:
Для будь-якого многочлена ![]() степеня
існує таке розширення L
поля
Р, в якому
розкладається на лінійні множники.
степеня
існує таке розширення L
поля
Р, в якому
розкладається на лінійні множники.
Означення 1: Поле L, в якому многочлен розкладається на лінійні многочлени, називають полем розкладу цього многочлена.
Приклад 1.
не
розкладається на множники ![]() в.
в.
![]() в
кінці многочленів над полем чисел виду
в
кінці многочленів над полем чисел виду
![]() в кінці многочленів
в кінці многочленів
![]() над
полем
R
дійсних
чисел
над
полем
R
дійсних
чисел
![]()
![]()
![]() над
полем
дійсних
чисел, всі множники лінійні, тому С поле
розкладу.
над
полем
дійсних
чисел, всі множники лінійні, тому С поле
розкладу.
Означення 2: Поле Р називається алгебраїчно замкнутим, якщо воно є полем розкладу для будь-якого многочлена ненульового степеня.
Приклад: поле С комплексних чисел. Твердження про алгебраїчну замкненість цього поля основна теорема теорії многочленів.
Наслідок 1: Многочлен n-го степеня має у полі розкладу n коренів.
Наслідок
2: У
полі розкладу многочлен ![]() має
канонічний розклад виду
має
канонічний розклад виду ![]() ,
де
,
де
![]() різні корені многочлена
.
різні корені многочлена
.
Теорема
5 (Вієта): Якщо
корені многочлена ![]() ,
то
,
то
![]() ,
,
![]() ,
(3)
,
(3)
……………………………………………………………………………………
![]()
…………………………………………………………………………………….
![]()
Символ
![]() cлід
тут
розмістити так, що сума береться по всіх
cлід
тут
розмістити так, що сума береться по всіх
![]() комбінаціях
з n індексів 1,2,3,…,
n
по
k.
комбінаціях
з n індексів 1,2,3,…,
n
по
k.
Для доведення формул (3) досить виконати множення у правій частині рівності:
![]()
