Дії над многочленами.

Нехай дано два многочлени над областю цілісності R.

( К , (8)

( ) (9)

Означення 1.

Многочлени називають рівними між собою і записують , якщо канонічні форми цих многочленів збігається ,тобто

(10)

Рівність многочленів має властивості рефлексивності ,симетричності та транзитивності,тобто є відношенням еквівалентності на множині К[x] .

Означення 2.

Сумою многочленів називається многочлен:

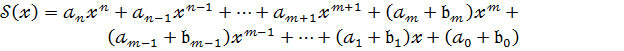(11).

Те ,що є сумою многочленів записують так:

Н1.

Якщо є К[ ] , К[ ] , то й

Н2.

Степінь суми двох многочленів не перевищує більшого зі степенів даних многочленів :

deg

Н3.

Для довільного многочлена К[ ] і К[ ]

(12)

Означення 3.

Добутком многочленів (8 і 9) називається многочлен:

(13)

де

( ),

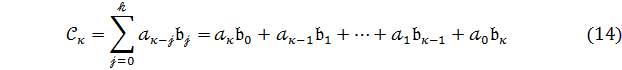
Те що є добутком многочленів , записують так:

.

Наведене означення є безпосереднім узагальненням «шкільного» правила множення многочленів.

Вираз (14) можна переписати :

.

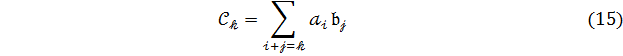
Н4:

Якщо є К[ ], є К[ ],то й є К[ ]

Н5:

Якщо не є нуль-многочлени ,то deg ( )=deg deg . (16)

Н6:

При множені двох многочленів,з яких хоч один нуль-многочлен дістаємо нуль-многочлен.

(17)

Теорема 1:

Сукупність К[ ] усіх многочленів над областю цілісності К є область цілісності відносно операції додавання та множення многочленів.

Доведення:

З наслідків 1 та 4 випливає що сукупність К[ ] є комутативне кільце відносно заданих операцій:

1.

2. тому , що є комутативне кільце і

3.Асоціативність додавання многочленів.

Розглянемо три многочлени:

[ ]+ (18)

випливає безпосередньо з асоціативності додавання елементів у кільці К.

За означенням рівності многочленів співвідношення (18) рівносильне степені рівностей:

(

4.Нульовим елементом в К[ ] є очевидно нуль многочлен

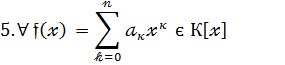
Існує в К[ ] протилежний

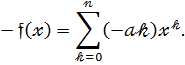
6.Для перевірки асоціативності множення многочленів :

Якщо коефіцієнт многочлена то відповідно до (15)

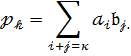
Але тоді й коефіцієнт многочлена :

є

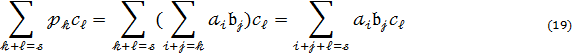
З другого боку позначаючи через й коефіцієнт многочлена

Дістаємо для коефіцієнта многочлена такий вираз :

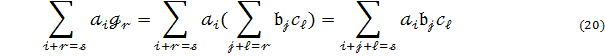
Зіставляючи (19) і (20) переконуємось що асоціативність виконується.

7.Дистрибутивний закон

[ ] випливає з рівності

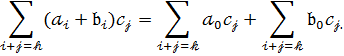
Отже К[ ] – комутативне кільце.

Покажемо , що К[ ] – область цілісності, тобто не існує в ньому дільників нуля.

Нехай є К[ ].

старші коефіцієнти .

має старший коефіцієнт ,тому не є нуль многочленом.

2.Подільність в К[ ].

Слід показати ,що для довільних многочленів можна подати у вигляді:

(1)

Де ,або deg Тут ділене , дільник , частка,

Степінь остачі повинен бути менший за степінь дільника.

Приклад 1 : Нехай f(х)= х²-3х+1, g(х)=х²+1. Рівність х³-3х+1=(х²+1)х+(-4х+1) свідчить, що f(х) ÷ на g(х) з остачею. Частина S(х)=х, остача r(х) =-4х+1. Так само g(х) ділиться на f(х) з остачею: х²+1=0*(х³-3х+1)+х²+1. S₁(х)=0 – частка, r₁(х)=х²+1 – остача.

Теорема ( про ділення з остачею в К[х]), де К-поле. Будемо вимагати, щоб К була полем, тобто, щоб в К існувала одиниця і для довільного елемента а≠0 існував обернений елемент а^-1.

Сукупність всіх многочленів над полем Р є область цілісності з одиницею Р[х] відносно додавання і множення многочленів.

Теорема 1 : Довільний многочлен f(х) з кільця Р[х] ділиться з остачею на будь-який многочлен g(х) з цього кільця, відмінний від 0 многочлена, при цьому частина й остача також належать до Р[х] і визначаються однозначно.

Доведення: Встановимо можливість знайти серед многочленів з кільця Р[х] частку S(х) і остачу r(х) для будь-яких многочленів f(х)= g(х) є Р[х] при g(х)≠0. Нехай f(х)= а_nхⁿ+a_n-1 x^n-1+…+a₁x+a_0, g(х) = b_mx^m + b_m-1x^m-1+…+b₁x+b₀.

Якщо f(х)=0, то S(х)=0, r(х)=0. Нехай n=deg f(х)<deg g(x)=m тоді S(x)=0, r(x)=f(x). Розглянемо n≥m.

Виконаємо доведення методом індукції по n, починаючи з n=0. При n=0, m=0, f(x)=a₀, g(x)=b₀≠0 тому S(x)= a₀/ b₀, r(x)=0. S(x) є P(x), бо a₀/b₀ є Р.

Припустимо, що теорема справедлива для всіх многочленів таких, що deg f <n і доведемо її для многочленів степеня n.

Розглянемо многочлен

Р(х)=f(x)=a_n/b_m x^n-m g(x) a_n≠0, b_m≠0.

Старший член многочлена а_n/b^m x^n-m g(x)=a_nxⁿ тобто старшому члену многочлена f(x). Тому deg P<n і за припущенням індукції Р(х) можна поділити з остачею на g(x);

P(x)= g(x)S₁(x) + r₁(x), S₁(x), r₁(x) є P[x], r₁(x)=0 або deg r₁<deg g.

Отже f(x)- a_n/b_m x^n-m g(x)= g(x)S₁(x) + r₁(x),

Звідси f(x)=g(x) S(x)+r(x), де r(x)=r₁(x), S(x)=S₁(x)+ a_n/b_m x^n-m, де S(x) і r(x) є P[x] і що r(x)=0, або deg r= deg r₁<deg g.

Цим показано можливість ділення f(x) на g(x) з остачею. Встановимо єдиність частки S(x) і остачі r(x). Припустимо, що можливі два записи:

f(x)= g(x)S(x)+ r(x), deg r<deg g;

f(x)= g(x)S^{^}(x)+r^{^}(x), deg r^{^}< deg g;

Віднімаючи другу рівність від першої, дістанемо:

g(x) [S(x)- S^{^}(x)]=r(x)- r^{^}(x). (2)

g(x)≠0 за умовою

Якщо припустити, що r(x) ≠ r^{^}(x), то й S(x) ≠ S^{^}(x) (адже Р[x] не має дільників нуля). Але приходимо до суперечливості. Справді права частина (2) є многочлен степінь якого менший від deg g і меншого від степеня лівої частини рівності (1). Отже (2) можлива коли коли r(x)= r^{^} (x) S(x)= S^{^}(x), частка єдина, остача єдина. Теорема доведена.

4. Ділення многочлена на лінійний двочлен. Схема Горнера. Теорема Безу. Розклад многочлена за степенями лінійного двочлена. Практичне здійснення ділення з остачею, для двох заданих многочленів ґрунтується на методі, використаному при доведенні теореми 1.

Приклад 1: Нехай f(x)=x⁴-2x³+x-1, a g(x)=x²-2

Знайдемо : g₁(x)=f(x)- a_n/b_m x^n-m g(x):

g₁(x)=x⁴-2x³+x-1-x² (x²-2)=-2x³+2x²+x+1 далі з g₁(x) так як з f(x);

g₂(x)=-2x³+2x²+x-1+2x(x²-2)=2x²-3x-1;

g₃(x)=2x²-3x-1-2(x²-2)=-3x+3

deg g₃(x)<deg g(x) і тому S(x)=x²-2x+2, r(x)= -3x+3.

X⁴-2x³+x-1=(x²-2)(x²-2x+2)+ (-3x+3)

Це можна записати :

X⁴-2x³+x-1 x²-2

Метод невизначених коефіцієнтів

X⁴-2x³+x-1=(x²-2)S(x)+r(x) (3)

cтепінь S(x)≤n-m=2 r(x)<m, deg r(x)=1.

S(x)=A₂x²+A₁x+A₀ r(x)=B₁x+B₀

Підставляючи вирази в рівність (3) маємо:

X⁴-2x³+x-1=(x²-2)(A₂x²+A₁x+A₀)+(B₁x+B₀) на підставі означення рівності многочленів коефіцієнти при однакових степенях Х рівні між собою. Звідси дістанемо:

A₂=1, A₁=-2, -2A₂+A₀=0, -2A₁+B₁=1, -2A₀+B₀=-1,

A₂=1, A₁=-2, A₀=2, B₁=-3, B₀=3

S(x)=x²-2x+2, r(x)=-3x+3

У загальному випадку S(x) шукають у вигляді многочлена з невизначеними коефіцієнтами степеня n-m, a r(x) - m-1

Нехай g(x)= х-2 – лінійний двочлен. Використаємо метод невизначених коефіцієнтів

a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀=(x-2)(A_n-1x^n-1+A_n-2x^n-2+…+A₁x+A₀)+r. r-const. (4)

Прирівнюючи коефіцієнти у (4) дістанемо:

а_n=A_n-1,

a_n-1=A_n-2- α A_n-1

……………………..

a₁=A₀- α A₁,

a₀= r- α A_0,

звідси

A_n-1= a_n

A_n-2= a_n-1+ α A_n-1

A_n-3=a_n-2+ α A

……………………..

A₀= a₁+ α A₁

r= a₀+ α A₀

Формули (5) показують, що поділити многочлен на х- α можна за такою схемою- схемою Горнера:

	аn	an-1	an-2	an-3	…	a1	a0
α	an An-1	αAn-1+an-1 An-2	αAn-2+an-2 An-3	αAn-3+an-3 An-4	…	αA1+a1 A0	αA0+a0 r

Виконуючи ділення з остачею за цією схемою, кожний наступний коефіцієнт А_к-1 частки й остачу r дістають множенням щойно обчисленого коефіцієнта А_к на α і додаванням до знайденого добутку відповідного коефіцієнта ак даного многочлена.

Приклад 2 : Поділимо за схемою Горнера многочлен х⁴-3х²+2х-1 на х-2 а₄=1, а₃=0, а₂=-3, а₁=2, а₀= -1, α=2.

	1	0	-3	2	-1
2	1	2	2*2-3=1	2*1+2=4	2*4-1=7

S(x)= x³+2x²+x+4, r=7

За схемою можна кілька раз ділити на один і той же лінійний двочлен

	1	0	-3	2	-1
2	1	2	1	4	7
2	1	4	5	22

Легко перевірити: остача при діленні f(x) на х- α дорівнює значенню многочлена при х= α тобто f(x). Це теорема Безу.

Т.Б для будь-якого елемента α з поля Р остача при діленні многочлена f(x) є P[x] на х- α= f(x).

Доведення : за формулою (1) ділення з остачею маємо:

f(x)=(х- α)S(x)+r, (6)

де многочлен r є константа, бо має степінь, нижчий від степеня х- α. Оскільки многочлени, що стоять у лівій і правій частинах (6) рівні між собою, то рівні між собою і їх значення при будь-якому х є Р. Тому взявши х= α, дістанемо f(α)=r, що й треба було довести.

За схемою Горнера зручно багато ділити многочлен на лінійний двочлен. За допомогою такого ділення легко дістати розклад довільного многочлена f(x) за степенями х- α.

Нехай f(x)- многочлен n-го степеня над полем Р, α-елемент цього поля. Ділення на х- α дає: f(x)=(х- α) f₁(х)+С₀, де (7)

f₁(х)-многочлен (n-1)-го степеня з Р[x], a C₀-елемент поля Р. Якщо n˃1 маємо :

f₁(x)=(x- α) f₂(x) + C₁ (8)

f₂(x)=(x- α)f₃(x)+C₂

……………………………

f_n-1(x)= (x- α)f_n(x)+C_n-1

f_n(x) є многочлен нульового степеня f_n(x)=C_n

Виключаючи з (7) і (8) f_n-1(x),f_n-2(x),…,f₂(x), f₁(x) дістанемо:

f(x)=C_n(x- α)ⁿ+C_n-1(x-α)^n-1+…+C₁(x-α)+C₀ (9)

Отже, многочлен f(x) над полем Р ми подали як многочлен такого самого степеня над тим самим полем, але вже від заміненого у=х- α. При цьому коефіцієнти С₀, С₁, …С_n однозначно визначаються через α коефіцієнти а_0, а₁, …,а_n многочлена f(х) . А саме, С₀ є остача від ділення f(х) першої частки f₁(x) на х- α і т.д. Що ж до C_n то ще є остання частка в процесі послідовного ділення.

Приклад 4: Знайдемо розклад многочлена f(x)=х⁵-3х³+х²-2х+1 за степенями двочлена х-1.

	1	0	-3	1	-2	1
1	1	1	-2	-1	-3	-2
1	1	2	0	-1	-4
1	1	3	3	2
1	1	4	7
1	1	5
1	1

С₅=1, С₄=5, С₃=7, С₂=2, С₁=-4, С₀=-2

f(х)= (х-1)⁵+5(х-1)⁴+7(х-1)³+2(х-1)²-4(х-1)-2.

****************************************************************

Лекція 2