Лекция 2 План лекции
Функции комплексного переменного.
Дифференцируемость и аналитичность.
Условия Коши-Римана.
2. Понятие и функции комплексного переменного.
Рассмотрим
две комплексные плоскости «W»
и «z»
(
;
).
Говорят, что на множестве Е плоскости «z» задана функция (W=f(z)), если указано правило, по которому каждой точке z из Е ставится в соответствие одна или несколько точек плоскости «W».
Если точка z пробегает значения множества Е, то точка W будет пробегать значения некоторого множества F.
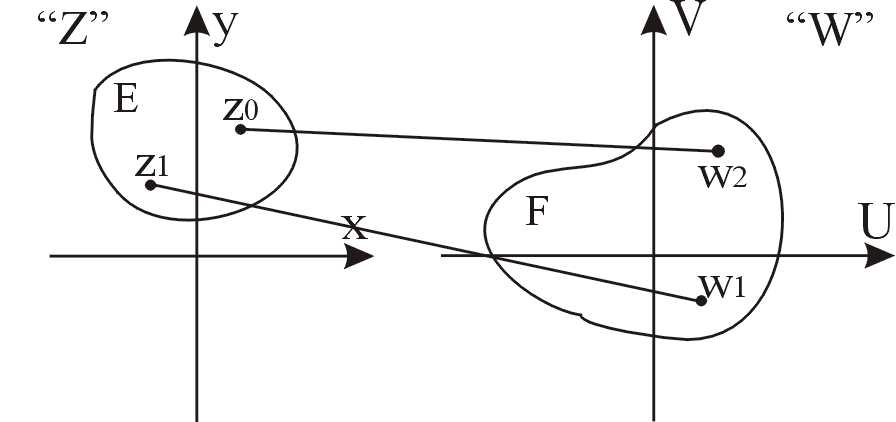Множество
Е – область определения функции f(z),
а множество F
– область
значения функции f(z).
Рис. 5
Если каждой точке z множества Е ставится в соответствие только одна точка F, то такая функция называется однозначной функцией, иначе многозначной.
Задание функции комплексного переменного эквивалентно заданию двух функций вещественного переменного.
.
3. Дифференцируемость и аналитичность.
Пусть
в некоторой окрестности точки
задана однозначная функция
.
Говорят, что существует предел функции
f(z)
при
(
),
если существуют следующие пределы
функции вещественного переменного:
,
.
При
этом число
называется пределом функции f(z)
при
,
т.е.
=
.
В
соответствии с определением предел не
зависит от того каким способом z
стремится
к
.
Поскольку предел функции комплексного
переменного сводится к двум пределам
вещественного переменного, то сохраняются
правила предельного перехода:
,
,
.
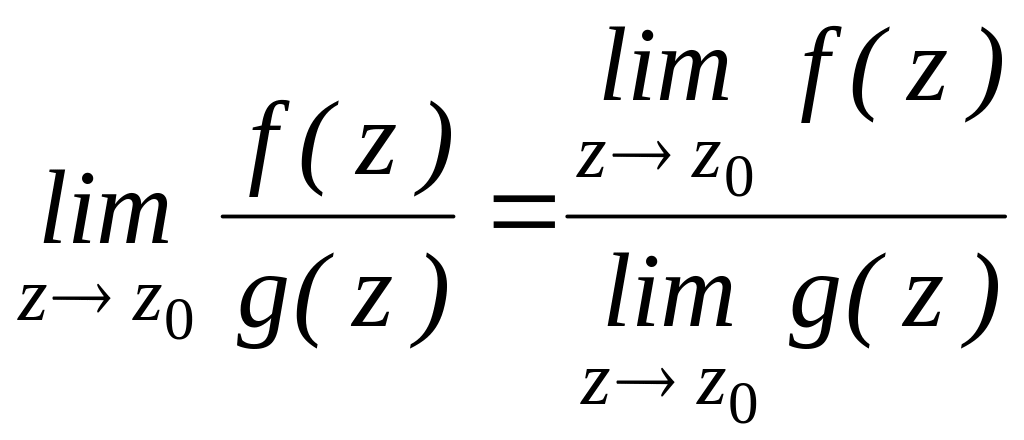Функция
f(z)
называется
непрерывной в точке
,
если
Функция
f(z)
называется
непрерывной в точке
,
если для
любого .>0
найдется такое (),
что из условия
следует, что
.
Функция
f(z)
называется
дифференцируемой в точке
,
если существует
предел
.
Рассмотрим условия, при которых функция f(z) является дифференцируемой. Пусть функция однозначно определена в окрестности точки z=x+iy.
Теорема 1. Для того чтобы функция была определена в точке z=x+iy необходимо и достаточно выполнение следующих условий:
в этой точке должны быть дифференцируемы функции U(x,y), V(x,y);
должны выполнятся условия Коши-Римана:
Докажем
необходимость. Предположим, что функция
f(z)
имеет точке
z
производную,
т.е. существует предел:
,
где h=s+it.
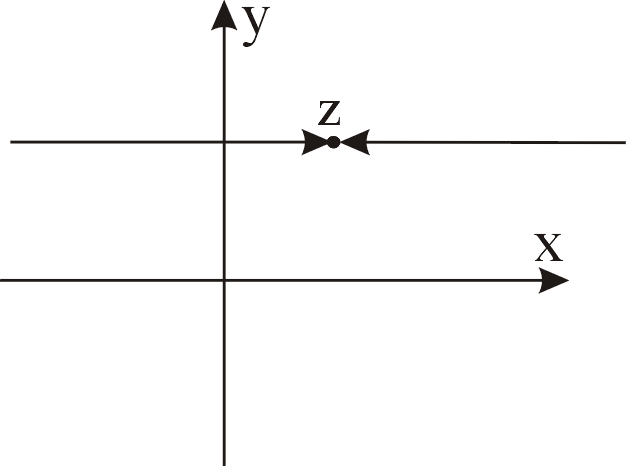
Воспользуемся независимостью предела
от способа стремления точки z+h
к точке z
(рис. 6). Положим h=s.
Рис. 6
По определению:
.
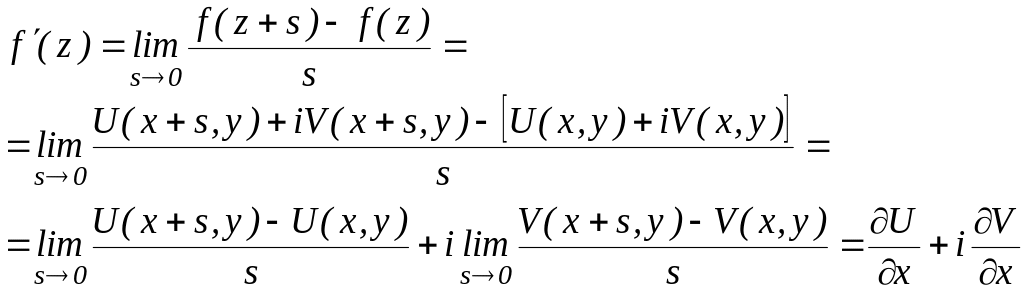
Примем, что точка z+h стремится к точке z вдоль прямой параллельной мнимой оси (h=it)(рис. 7).
Имеем:
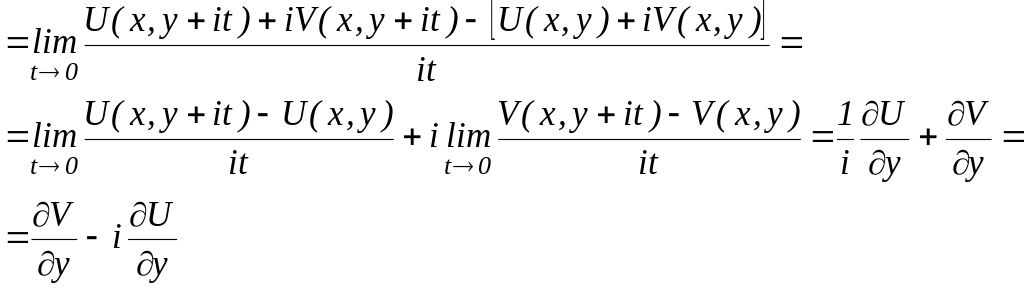
р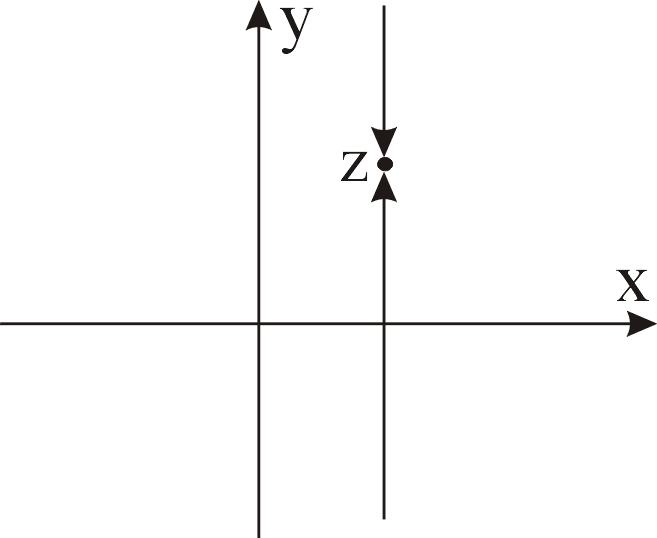
ис.7
,
.
Необходимость доказана, достаточность примем без доказательства.
С учетом условия Коши –Римана можно записать:
.
Поскольку для функций комплексного переменного сохраняются общие правила предельного перехода, то сохраняют свою силу и общие правила дифференцирования:
предельного перехода:
,
,
.
Функция f(z) называется аналитической в области D, если она дифференцируема в каждой точке области D.
Функция
f(z)
называется
аналитической
в точке а, если найдется такая окрестность
точки а:
,
в которой она дифференцируема.
Функция f(z) называется аналитической в области D, если она дифференцируема в каждой точке области D.