ГОСУДАРСТВЕННЫЙ КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ПО РЫБОЛОВСТВУ
МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСТЕТ
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ
ИЗМЕРЕНИЙ
Методические указания к практическим работам по дисциплине
«Метрология, стандартизация, сертификация» для специальности 271000 «Технология рыбы и рыбных продуктов» и специальности 271200
«Технология продуктов общественного питания»
.
Мурманск
УДК. [519.24 : 389.1] : 663/664 (07)
ББК 30.10 В 6
М- 34
Составитель – Ольга Александровна Николаенко, канд. техн. наук, доцент кафедры технологии рыбных продуктов Мурманского государственного технического университета, Сергей Юлианович Дубровин, канд. техн. наук, профессор той же кафедры
Рецензент: Петров Борис Федорович, канд. техн. наук, доцент кафедры технологии рыбных продуктов Мурманского государственного технического университета.
Методические указания рассмотрены и одобрены кафедрой технологии рыбных продуктов «15» января 2003г., протокол № 4
Мурманский государственный технический университет
Оглавление
-
Практическая работа 1. Определение грубых ошибок измерительного эксперимента и доверительных границ истинного значения измеряемой величины ……………………………
4
Практическая работа 2 Установление корреляционной зависимости между измеряемыми величинами……………………
11
Практическая работа 3. Проверка гипотезы о равенстве или различии измеряемых величин………………………………
21
Вопросы для самоконтроля…………………………………..
27
Рекомендованная литература………………………………….
27
|
4п 7 4
|
Практическая работа 1
Определение грубых ошибок измерительного эксперимента и
доверительных границ истинного значения измеряемой величины
Цель работы: научиться применять математические расчеты для контроля результатов измерений.
Задание:
1. Определить грубые ошибки из ряда измерений.
2. Определить среднее значение для ряда измерений и рассчитать доверительные границы истинного значения измеряемой величины.
3. Определить относительную погрешность для ряда измерений при заданной доверительной вероятности.
Теоретические сведения
Результат измерений – значение величины, полученное путем ее измерений. Результат измерений бывает неисправленный, исправленный и усредненный.
Неисправленный результат измерений – значение физической величины (ФВ), полученное при измерении до введения в него поправок, учитывающих систематическую погрешность.
Исправленный результат измерений - значение ФВ, полученное при измерении и уточненное введением в него необходимых поправок на действие систематических погрешностей.
Усредненный результат измерений – значение ФВ как среднее арифметическое значение кратного числа измерений.
К основным характеристикам качества измерений относятся точность, правильность, воспроизводимость и сходимость результатов измерений.
1. Точность измерений – качество измерений, отражающее близость результата измерений к истинному значению измеряемой величины.
2.Правильность измерений – качество измерений , отражающее близость к нулю систематической погрешности в их результате.
3.Сходимость результата измерений – близость друг к другу результатов измерений одной и той же величины, выполненных повторно одним и тем же средством измерений (СИ), одним и тем же методом в одних и тех же условиях и с одинаковой тщательностью.
4. Воспроизводимость результатов измерений - близость друг к другу результатов измерений одной и той же величины, полученных разными СИ, или разными методами, или в разных местах и разное время, или разными операторами.
Правильность измерений определяется погрешностью измерений – отклонением результата измерений от истинного (Хист) или действительного (ХД) значения измеряемой величины (Х изм).
Истинное значение ФВ применяют только в теоретических исследованиях. На практике используют действительное значение ФВ (ХД), тогда погрешность ΔХ изм. определяют по формуле:
ΔХ изм = Х изм - ХД
По способу проявления погрешности подразделяются на случайные, систематические, промахи, или грубые погрешности.
Систематическая погрешность измерений – составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же ФВ.
Случайная погрешность измерения – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и (или) значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же ФВ.
Грубая ошибка (промах) - это заведомо неправильный результат, возникающий в следствие нарушения основных условий измерения или в результате недосмотра экспериментатора.
Случайные погрешности не могут быть точно определены, но с помощью математической статистики и теории вероятности можно определить их пределы.
Основу теории случайных ошибок составляют предположения о том, что при большом числе измерений случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто; большие погрешности встречаются реже, чем малые (вероятность появления погрешности уменьшается с ростом ее величины); при бесконечно большом числе измерений истинное значение измеряемой величины равно среднеарифметическому значению всех результатов измерений, а появление того или иного результата измерений как случайного события или иного результата измерений как случайного события описывается нормальным законом распределения.
Из
теории вероятности известно, что наиболее
универсальным способом описания
случайных величин, является описание
их дифференциальных функций распределения,
т.е. плотности распределения вероятности
р(х)=dF(х)/d(х). Она всегда неотрицательная
и подчиняется условию нормирования:
.
(р – вероятное события). Достоверное
событие имеет вероятность р = 1, невозможное
р = 0. Для случайного события
,
а сумма вероятностей всех возможных
значений равна 1.
Зависимость вероятности р ожидания отдельных значений случайной величины от самих этих значений называется функцией распределения или рассеивания. Функция распределения может иметь любую форму. Наиболее часто в качестве модели распределения случайных погрешностей применяется нормальный закон распределения.
Мерой рассеивания результатов измерений является дисперсия, которая вычисляется по формуле:
, (1.1)
где
m(x)
– математическое ожидание,
,
хi
- множество возможных значений
Значительно чаще в качестве меры рассеивания используется среднее квадратическое отклонение:
(1.2.)
Чем
меньше
,
тем меньше рассеяние, тем больше
сходимость результатов измерений.
Для большой выборки и нормального закона распределения.
, (1.3.)
где
n
– число измерений
- среднее арифметическое значение
измеряемых величин.
Несмотря на то, что истинное значение измеряемой величины остается неизвестным, при помощи математической статистики модно определить пределы области вокруг экспериментально найденного значения измеренной величины, внутри которой следует ожидать с заданной степенью вероятности нахождение истинного значения. Эта область называется доверительным интервалом. Доверительный интервал характеризует точность измерений.
Доверительные границы погрешности результата измерений (μ) – наибольшее и наименьшее значение погрешности измерений, ограничивающее интервал, внутри которого с заданной вероятностью находится искомое значение погрешности результата измерений.
Ширина доверительного интервала зависит:
от величины рассеивания результатов измерений (зависит от числа измерений);
-от доверительной вероятности утверждения (доверительной вероятности).
Достоверность измерений (доверительная вероятность) рд –это вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал. Эта величина определяется в долях или в процентах, для технологических расчетов она, обычно, принимается равной 0,95. Это означает в заданный доверительный интервал из 100 измерений в доверительный интервал попадают 95. Значение (1-рД) – называется уровнем значимости. Из него следует, что при нормальном законе распределения погрешность, превышающая доверительный интервал, будет встречаться один раз из n измерений, где n = рД / (1-рД)
Если число измерений меньше 30, половина доверительного интервала определяется по формуле:
, (
1.4)
где t – критерий Стьюдента (таблица 1.1).
Если обозначить
,
(1.5)
тогда
, (1.6)
а действительное значение измеряемой величины равно:
(1.7)
Доверительный интервал:
(1.8)
Таблица 1.1 – Коэффициенты Стьюдента
n |
РД |
|||
0,80 |
0,90 |
0,95 |
0,99 |
|
2 |
3,080 |
6,310 |
12,710 |
63,700 |
3 |
1,886 |
2,920 |
4,300 |
9,920 |
4 |
1,638 |
2,350 |
3,188 |
5,840 |
5 |
1,533 |
2,130 |
2,770 |
4,600 |
6 |
1,476 |
2,020 |
2,570 |
4,030 |
7 |
1,440 |
1,940 |
2,450 |
3,710 |
8 |
1,415 |
1,860 |
2,360 |
3,500 |
9 |
1,397 |
1,830 |
2,310 |
3,360 |
10 |
1,383 |
1,800 |
2,260 |
3,250 |
Относительная погрешность результатов серии измерений при заданной доверительной вероятности определяют по формуле:
(1.9)
При обработке результатов измерений возникает необходимость исключить грубые ошибки измерений ( промахи) - заведомо неправильный результат, возникающий в следствие нарушения основных условий измерения или в результате недосмотра экспериментатора. Грубые ошибки необходимо отбрасывать. Внешним признаком результата, содержащего грубую ошибку, является его резкое отличие по величине от остальных значений.
Грубые ошибки отбраковываются путем расчета специальных критериев.
1 способ:
Пусть имеется число измерений (n+1), n не вызывают сомнения, одно нарушает ряд измерений. Все измерения выстраивают в порядке возрастания, тогда сомнительный результат будет Х п+1 или Хп-1
Находим среднее арифметическое значение n измерений:
(1.10)
Определяем среднюю квадратическую погрешность:
(1.11)
Исходя из степени достоверности, которая должна быть обеспечена, зададимся вероятностью Р того, что значение / Хп+1-Х/ не превышает некоторого значения ε (допустимое значение интервала), которое определим по формуле
ε = t σ (1.12)
Если / Хп+1-Х/ > ε результат Хп+1- подлежит исключению.
Например: получили результаты 81,80,80,82,87.
=
80,8
σ = 0,96
ε = 2,35 * 0,96 = 2,26
87-82 > 2,26; 87 – промах, исключается при обработке результатов
2 способ. С использованием критерия Диксона.
Все измерения располагают в порядке возрастания
Если величина, которая вызывает сомнение Х1, то Кд определяют по формуле:
(1.13)
Если величина, которая вызывает сомнение Хn+1, то Кд определяют по формуле:
(1.14)
Если Кд больше табличного значения Zp (таблица 1.2), которое определяется в зависимости от доверительной вероятности Р и числа степеней свободы (n-1), то результат, который вызывает сомнение в расчет не берут.
Например. Располагаем ряд измерений по возрастанию: 80,80,81,82,87
0,71
При доверительной вероятности 0,95 и числе степеней свободы 4
Zp = 0,64; 0,71>0,64 , значит 87 – промах.
Таблица 1.2
Число степеней свободы (n-1) |
Zp при Р |
||
0,90 |
0,95 |
0,99 |
|
3 |
0,58 |
0,75 |
0,89 |
4 |
0,56 |
0,64 |
0,78 |
5 |
0,48 |
0,56 |
0,70 |
6 |
0,35 |
0,41 |
0,53 |
3 способ. С использованием критерия
Шовине, который используют, если число
измерений невелико (не более 10). В этом
случае промахом считается результат
Хi, если разность |
-Xi| превышает значение
,
приведенные ниже в зависимости от числа
измерений:
| -Xi| › 1,6 при n = 3
| -Xi| › 1,7 при n = 6
| -Xi| › 1,9 при n = 8
| -Xi| › 2,0 при n = 10
Порядок выполнения работы
1. В соответствии с задания по формулам 1.9 – 1.14 вычислить и исключить грубые погрешности (промахи) из серии измерений.
1. По формулам 1.1.-1.7 вычислить доверительных границ истинного значения измеряемой величины
1. По формуле 1.8 вычислить относительные погрешности в сериях измерений. Результаты обработки данных занести в таблицу 3
Таблица 1.3 – Результаты обработки данных
i |
Хi |
Х2 |
Х3 |
Х4 |
Х5 |
|
σ |
μ |
Хд |
|
|
|
|
|
|
|
|
|
|
Практическая работа 2
Установление корреляционной зависимости между
измеряемыми величинами
Цель работы: научиться применять математические расчеты для установления корреляционной зависимости между измеряемыми величинами.
Задание:
1. Определить среднее арифметическое значение физической величины из ряда равноточных измерений.
2. Определить значение коэффициента корреляции между значениями двух физических величин.
Теоретические сведения
Корреляционный анализ изучает усредненный закон поведения каждой из двух величин в зависимости от значений другой величины. Меру этой зависимости количественно устанавливает коэффициент корреляции (r).
Корреляция называется линейной, если обе функции регрессии y=f(x) b x=f(y) линейны. В этом случае мерой линейной зависимости между величинами служит коэффициент корреляции первого порядка (линейный).
Коэффициент корреляции по абсолютной величине всегда меньше или равен -1≤ | r | ≤ 1.
Если r=0, то это значит, что линейная функция отсутствует, но возможно существование нелинейной.
Чем | r | ближе к 1, тем теснее линейная зависимость между у и х.
Если | r | = 1 , то существует линейная функциональная зависимость между величинами, т.е. каждому значению одной величины соответствует точно одно значение другой величины.
О степени взаимозависимости между величинами судят по абсолютной величине коэффициента корреляции:
| r | < 0,39 |
- нет корреляции |
0,40 ≤ | r | < 0,60 |
- средняя корреляция |
0,60 ≤ | r | ≤ 0,80 |
- значительная корреляция |
| r |> 0,80 |
- высокая корреляция |
Положительное значение r означает, что с увеличением одной величины, другая тоже возрастает. Отрицательное значение r означает, что с увеличением одной величины, другая уменьшается.
Коэффициент корреляции рассчитывается по формуле:
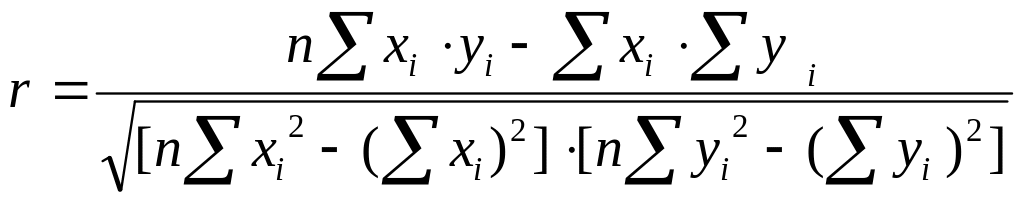(2.1)
где n – число измерений.
Достоверность коэффициента корреляции tr определяют по формуле:
tr = r/mr, (2.2)
где mr – ошибка коэффициента корреляции, которая определяется по формуле:
(2.3)
где N – количество элементов в выборке (количество точек измерений).
Полученное значение tr сравнивают со стандартным значением критерия Стьюдента tS (таблица 3.1).
Таблица 3.1 Стандартным значением критерия Стьюдента при вероятности 0,95 и числе степеней свободы f = N-2
f |
tS |
f |
tS |
1 |
12,7 |
6-7 |
2,4 |
2 |
4,3 |
8-9 |
2,3 |
3 |
3,2 |
10-13 |
2,2 |
4 |
2,8 |
14-28 |
2,1 |
5 |
2,6 |
29 и более |
2,0 |
Если tr › tS, то коэффициент корреляции значим.
Пример: имеется статистический ряд парных измерений
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
8 |
11 |
14 |
16 |
21 |
26 |
27 |
32 |
34 |
41 |
Необходимо определить коэффициент корреляции. Расчет целесообразно вести в табличной форме (таблица 2.2)
Таблица 2.2. Расчет уравнения
х |
у |
х2 |
у2 |
ху |
1 |
8 |
1 |
64 |
8 |
2 |
11 |
4 |
121 |
22 |
3 |
14 |
9 |
196 |
42 |
4 |
16 |
16 |
256 |
64 |
5 |
21 |
25 |
441 |
105 |
6 |
26 |
36 |
676 |
156 |
7 |
27 |
49 |
729 |
189 |
8 |
32 |
64 |
1024 |
256 |
9 |
34 |
81 |
1156 |
306 |
10 |
41 |
100 |
1681 |
410 |
55 |
230 |
385 |
6344 |
1558 |
Коэффициент корреляции согласно (2.1)
