Тема 12

Задачі, що приводять до поняття похідної. Означення похідної. Фізичний та геометричний зміст похідної. Таблиця похідних. Похідна складеної та оберненої функцій

Відношення приросту у функції у = f(x) до приросту незалежної змінної х називається диференціальним відношенням:

Функція у = f(x) називається диференційовною в точці х = х₀, якщо існує границя

.

Похідні основних елементарних функцій

1. Похідна степеневої функції

.

2. Похідна показникової функції

3. Похідна логарифмічної функції

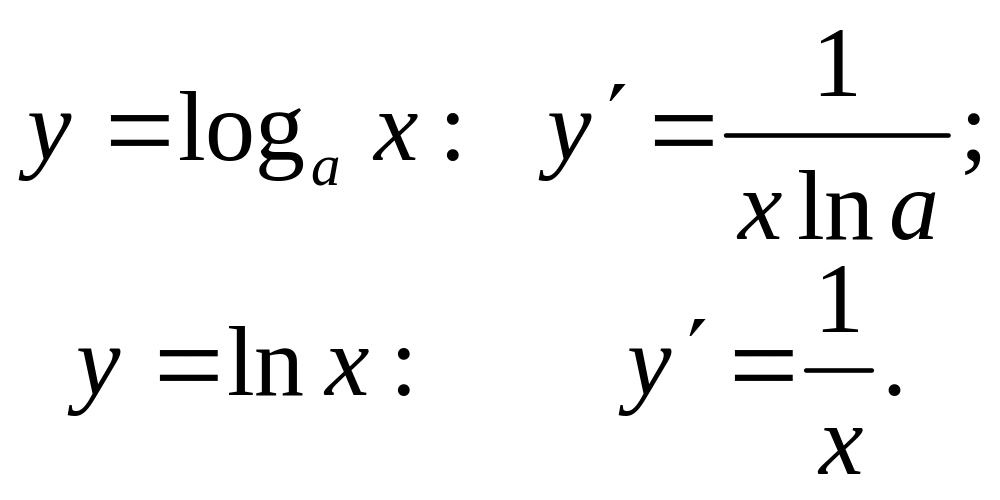
4. Похідні тригонометричних функцій

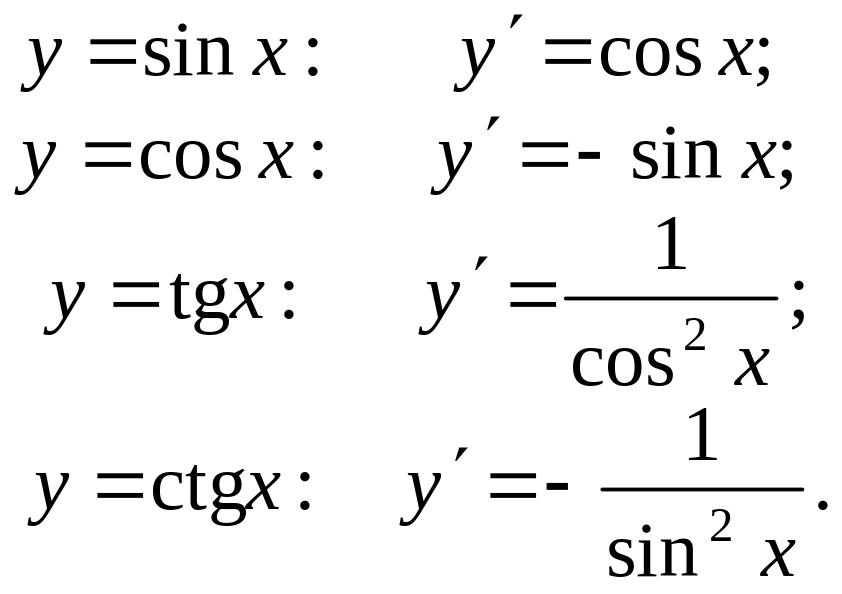
Похідна оберненої функції

Теорема 1. Якщо функція у = f(x) монотонна й має в точці х відмінну від нуля похідну, то функція, обернена до даної, подається у вигляді х = g(y) і має похідну х = g(y), обернену до похідної даної функції:

.

Тема 13

Диференціал функції, його геометричний зміст. Властивості. Застосування диференціала в наближених обчисленнях

Означення. Величина f(x)х називається диференціалом функції f(x) за приростом х.

Диференціал є лінійним наближенням (апроксимацією) до приросту функції: . Наскільки менше , настільки краще наближення.

Правила обчислення диференціала

Правило 1. Нехай .

Тоді

або

Правило 2. Дано .

Тоді

Правило 3. Маємо , .

Тоді

Правило 4. Якщо , , то

Правило 5. Якщо функція має обернену , то

.

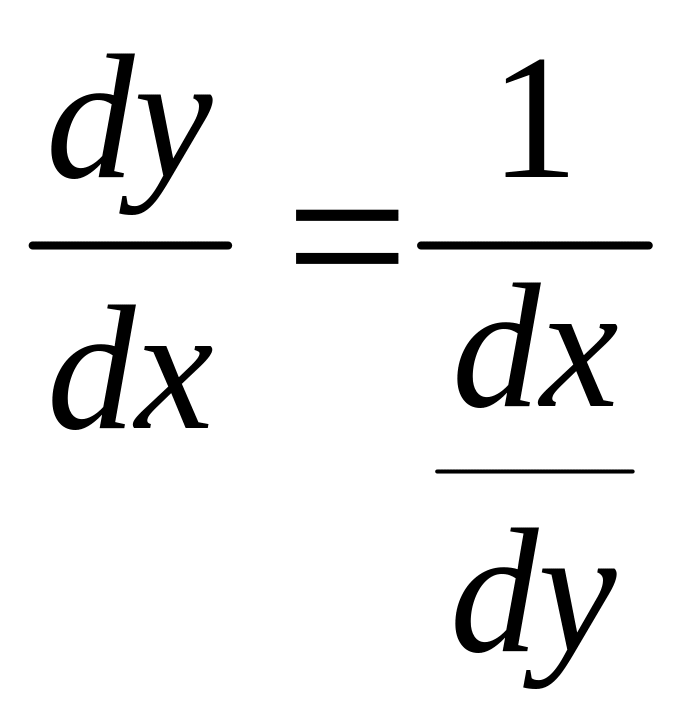Правило 6. Якщо функції задані у параметричному вигляді

, ,

то

.

Другим диференціалом функції у = f(x) називається вираз d(dy).

Тема 14

Формула Тейлора

Теорема. Нехай функція f(x) має в -околі точки х₀ (n + 1) похідну. Тоді для будь-якої точки х із цього околу знайдеться точка с, розміщена між точками х і х₀, для якої справджується рівність:

(1)

де Т(х) — п-й многочлен Тейлора функції f(x) у точці х₀.

Формулa Маклорена:

Тема 15

Застосування диференціального числення до дослідження функцій

Лекція „Загальний план дослідження функції”

1. Знайти область визначення та значення функції, заданої формулою, якщо таку область не зазначено.

2. Дослідити функцію на парність, непарність, періодичність.

3. З’ясувати точки перетину функції з вісями координат.

4. Дослідити функцію на неперервність.

5. Знайти асимптоти графіка функції (якщо вони існують).

6. З’ясувати, як функція поводиться на кінцях кожного з проміжків області визначення (знайти границі функції на кінцях цих проміжків, якщо вони є).

7. Дослідити функцію на диференційовність.

8. Дослідити функцію на монотонність та екстремуми. Знайти екстремуми і значення функції в точках екстремуму.

9. Дослідити функцію на опуклість (вгнутість): знайти інтер­вали опуклості (вгнутості), а також точки перегину функції.

10. Знайти найбільше і найменше значення функції (якщо вони існують).

11. Побудувати графік функції.

Тема 16

Функція багатьох змінних. Означення та символіка. Границя функції. Графік функції

Графіком функції двох змінних називається множина всіх точок (х, у, f(x, y)) простору R³, де (x, y)  R².

Лінією рівня називається множина всіх точок площини, в яких функція набуває однакових значень. Рівняння ліній рівня записують у вигляді . Для функції трьох змінних розглядають поверхні рівня

Число А називається границею функції при , , якщо для будь-якого існує число , таке, що в разі виконання нерівності

справджується нерівність .

Теорема 1. Якщо функція f(х, y) має границю при (х, y)   (х₀, y₀), то така границя тільки одна.

Теорема 2. Якщо функція f(х, y) має границю при (х, y)   (х₀, y₀), то вона обмежена в деякому околі точки f(х₀, y₀).

Теорема 3. Якщо , і в деякому виколотому околі точки ( , y₀) виконується нерівність , то .

Теорема.4. Якщо і в деякому виколотому -околі точки ( , y₀) справджуються нерівності , то і .

Теорема 5. Якщо ,

Теорема 1.6. Нехай на множині D визначено складену функ­цію , де , і нехай функції , неперервні в точці , а функція неперервна в точці , де , . Тоді складена функція неперервна в точці