
- •Диференціальні рівняння з частинними похідними першого порядку. Звязок з системою звичайних диференціальних рівнянь у симетричній формі.
- •Класифікація диференціальних рівнянь з частинними похідними іі порядку для випадку двох і багатьох незалежних змінних.
- •Види топологічних просторів. Топологія, індукована метрикою.
- •Поняття метричного простору. Простір ізольованих точок. Метричні простори r1, r(n), c[a,b].
- •Граничні точки, точки дотику, замикання множини. Сепарабельні простори. Послідовність в метричному просторі. Границя послідовності.
- •Стискаючі відображення, їх неперервність. Теорема Банаха, її геометричне тлумачення.
- •Поняття лінійного простору. Приклади. Лінійна залежність і лінійна незалежність елементів. Нескінченно - вимірні простори. Підпростори.
- •Означення і приклади нормованих просторів. Означення евклідових просторів. Нерівність Буняковського - Коші.
- •Означення і приклади лінійних операторів. Неперервність і обмеженість. Норма операторів. Сума і добуток операторів. Обернений оператор, оборотність.
- •Бінарні відношення. Рефлексивні, симетричні, транзитивні бінарні відношення. Класи еквівалентності, фактор–множина.
- •Бінарні відношення порядку, його властивості. Мінімальні та максимальні елементи. Впорядковані множини.
- •Групи. Приклади груп. Основні властивості груп.
- •Ізоморфізм та гомоморфізм груп. Його властивості.
- •Кільце, приклади кілець. Основні властивості кілець. Ізоморфізм та гомоморфізм груп
- •Поле. Приклади полів, основні властивості полів. Ізоморфізм та гомоморфізм полів.
- •Поле комплексних чисел. Комплексні числа, алгебраїчна форма комплексних чисел.
- •Неперервні відображення топологічних просторів і їх властивості. Гомеоморфізм.
- •Теорема Ейлера для многогранників.
- •Суть сучасного аксіоматичного методу. Основні вимоги до системи аксіом. Поняття про інтерпретацію системи аксіом.
- •Точково–векторна аксіоматика Вейля трьохвимірного евклідового простору і її несуперечливість.
- •Вимірювання многокутників. Площа многокутника і її аксіоми. Теорема існування і єдиності.
- •Рівноскладеність і рівновеликість многокутників і многогранників.
- •Аксіоматика площини Лобачевського. Абсолютна геометрія. Паралельні напрямлені прямі на площині Лобачевського і їх властивості.
- •Взаємне розміщення прямих на площині Лобачевського. Теорема про існування розбіжних прямих і наслідки з неї. Критерій розбіжності двох прямих.
- •Трикутники на площині Лобачевського.
- •Незалежність аксіоми паралельності від решти аксіом д. Гільберта.
Диференціальні рівняння з частинними похідними першого порядку. Звязок з системою звичайних диференціальних рівнянь у симетричній формі.
Диференціальним
рівнянням І порядку з частинними
похідними
наз. співвідношення, яке зв’язує між
собою незалежні змінні, шукану функцію
і похідні І порядку від шуканої функції.
![]() .
(0)
.
(0)
Рівняння
(0) наз. лінійним,
якщо функція
![]() є лінійною по відношенню до шуканої
функції
є лінійною по відношенню до шуканої
функції
![]() та її частинних похідних.
та її частинних похідних.
Розв’язок
відповідного однорідного рівняння
![]() (1) шукаємо, враховуючи існування
незалежних інтегралів системи звичайних
диференціальних рівнянь записаній в
симетричній формі
(1) шукаємо, враховуючи існування
незалежних інтегралів системи звичайних
диференціальних рівнянь записаній в
симетричній формі
![]() .
(2)
.
(2)
Система (2) наз. відповідною однорідному рівнянню (1).
Коефіцієнти
![]() є визначеними і неперервними разом з
похідними 1-го порядку по змінних
є визначеними і неперервними разом з
похідними 1-го порядку по змінних
![]() і одночасно
і одночасно
![]() нулю в околі деякої точки
нулю в околі деякої точки
![]() .
.
Наприклад,
нехай
![]() ,
тоді як відомо з курсу диф. рівнянь
система (2) має єдиний розв’язок і для
даної системи існують
,
тоді як відомо з курсу диф. рівнянь
система (2) має єдиний розв’язок і для
даної системи існують
![]() незалежних інтегралів.
незалежних інтегралів.
Дійсно, систему (2) можна переписати у нормальній формі:
![]() Відмітимо,
що кожний інтеграл системи (2) є розв’язком
рівняння (1) і
Відмітимо,
що кожний інтеграл системи (2) є розв’язком
рівняння (1) і
![]() навпаки
кожний розв’язок
рівняння (1) є інтегралом системи (2).
навпаки
кожний розв’язок
рівняння (1) є інтегралом системи (2).
………..
Дійсно,
нехай
![]() - інтеграл системи (2). Тоді повний
- інтеграл системи (2). Тоді повний
![]() диференціал
даного виразу дорівнює
диференціал
даного виразу дорівнює
![]()
![]()
![]() .
Поділимо на диференціал
.
Поділимо на диференціал
![]() :
:
![]()
![]()
![]() .
Враховуючи систему в нормальній формі:
.
Враховуючи систему в нормальній формі:
![]()
![]() .
Домножимо рівняння на коефіцієнт
.
Домножимо рівняння на коефіцієнт
![]() :
:
![]()
![]()
![]() .
Останній вираз – це однорідне ДРЧП І
порядку для ф-ції
.
Останній вираз – це однорідне ДРЧП І
порядку для ф-ції
![]() ,
де
- розв’язок.
,
де
- розв’язок.
Якщо
відомо
незалежних інтегралів системи (2), то
загальний розв’язок однорідного
рівняння записується у вигляді:
![]() ,
де
,
де
![]() - незалежні інтеграли, ф - ція
- довільна ф-ція, неперервна разом з
похідними 1-го порядку.
- незалежні інтеграли, ф - ція
- довільна ф-ція, неперервна разом з
похідними 1-го порядку.
Лінійне неоднорідне рівняння в загальному має вигляд:
![]() (3)
(3)
Розв’язок
р-ня (3) шукаємо в неявній формі
![]() ,
де
,
де
![]()
![]() ,
,
![]() .
Виразимо
.
Виразимо
![]()
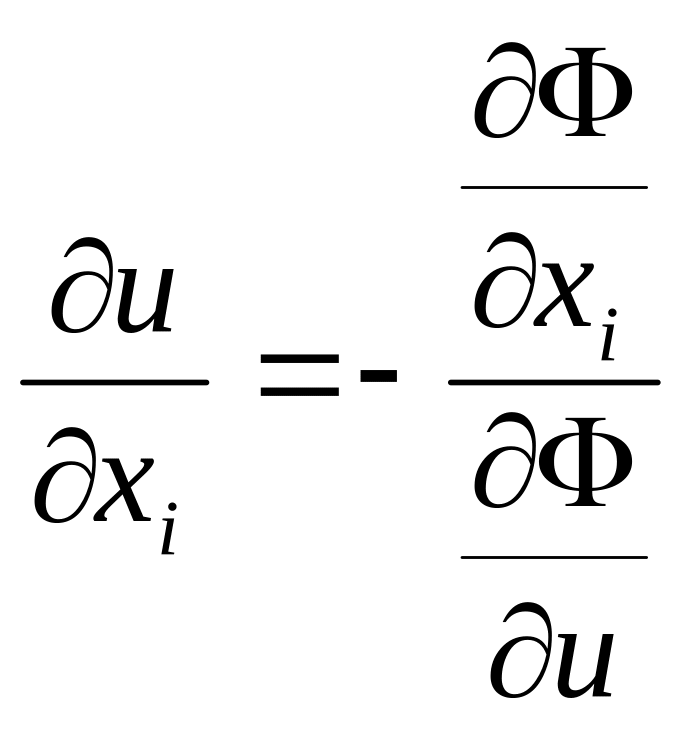 і підставляємо в р-ня (3), помножимо на
і підставляємо в р-ня (3), помножимо на
![]() ,
поміняємо знак. Отримаємо:
,
поміняємо знак. Отримаємо:
![]() .
.
Останній
вираз є однорідним диференціальним
рівнянням відносно функції
.
Система в симетричній формі:
![]() .
Така симетрична система повинна мати
.
Така симетрична система повинна мати
![]() - незалежних інтегралів
- незалежних інтегралів
![]() .
А далі все як для однорідної системи.
.
А далі все як для однорідної системи.
![]() -
загальний розв’язок
для неоднорідного рівняння.
-
загальний розв’язок
для неоднорідного рівняння.
Класифікація диференціальних рівнянь з частинними похідними іі порядку для випадку двох і багатьох незалежних змінних.
Диференціальним рівнянням з частинними похідними ІІ порядку наз. співвідношення, що зв’язує невідому ф-цію, похідні від шуканої ф-ції до ІІ порядку включно.
Наприклад,
для випадку двох просторових змінних
лінійного рівняння двох змінних має
вигляд
![]() (1),
(1),
![]()
![]()
![]()
![]() .
Підберемо нові змінні
.
Підберемо нові змінні
![]() так, щоб
рівняння (1) набувало більш простої
форми:
так, щоб
рівняння (1) набувало більш простої
форми:
![]() ,
,
![]() .
Знайдемо запис рівняння (1) в нових
змінних
.
Знайдемо запис рівняння (1) в нових
змінних
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Очевидно,
що нові змінні
є лінійними функціями
,
то другі похідні (![]() )
дорівнюють нулю. Підставляючи значення
в рівняння (1) отримаємо:
)
дорівнюють нулю. Підставляючи значення
в рівняння (1) отримаємо:
![]() (2).
Очевидно, що рівняння набуває більш
простої форми, якщо один із коефіцієнтів
рівняння дорівнює нулю. Наприклад,
(2).
Очевидно, що рівняння набуває більш
простої форми, якщо один із коефіцієнтів
рівняння дорівнює нулю. Наприклад,
![]() .
.
![]() .
.
Останнє
рівняння є рівнянням з частинними
похідними І порядку відносно ф-ції
![]()
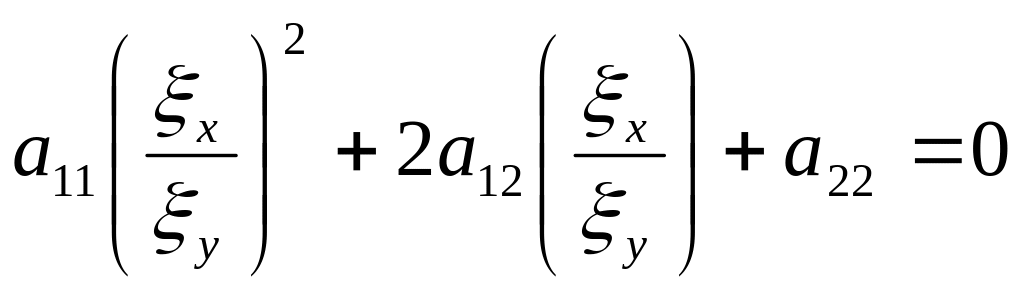 .
Це квадратне рівняння відносно
.
Це квадратне рівняння відносно
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() - звичайні диференціальні рівняння.
- звичайні диференціальні рівняння.
Розв’язки
останнього рівняння залежать від знака
підкореневого виразу
![]() .
У зв’язку
з цим вводиться класифікація рівнянь
з частинними похідними ІІ порядку.
.
У зв’язку
з цим вводиться класифікація рівнянь
з частинними похідними ІІ порядку.
![]() наз.
дискримінантом
рівняння (1).
наз.
дискримінантом
рівняння (1).
Якщо
![]() ,
то рівняння (1) наз. рівнянням
гіперболічного типу.
Має дві дійсних характеристики
(розв’язки), канонічна форма:
,
то рівняння (1) наз. рівнянням
гіперболічного типу.
Має дві дійсних характеристики
(розв’язки), канонічна форма:
![]() ,
де
,
де
![]()
Якщо
![]() ,
то рівняння (1) наз. рівнянням
параболічного типу.
Має одну дійсну характеристику, канонічна
форма:
,
то рівняння (1) наз. рівнянням
параболічного типу.
Має одну дійсну характеристику, канонічна
форма:
![]() ,
де
,
де
![]()
Якщо
![]() ,
то рівняння (1) наз. рівнянням
еліптичного типу.
Має дві комплексно-спряжені характеристики,
канонічна форма (заміна
,
то рівняння (1) наз. рівнянням
еліптичного типу.
Має дві комплексно-спряжені характеристики,
канонічна форма (заміна
![]() ):
):
![]()
Розглянемо
рівняння з частинними похідними ІІ
порядку для випадку багатьох змінних
![]() ,
(4)
,
(4)![]() - відомі задані ф-ції,
- шукана ф-ція.
- відомі задані ф-ції,
- шукана ф-ція.
Фіксуємо
деяку точку області
і в даній точці для рівняння (4) складаємо
наступну квадратичну форму:
![]() (5).
(5).
Якщо
при зведенні квадратичної форми (5) до
суми квадратів лише один коефіцієнт
відрізняється знаком від інших, то
рівняння (4) в даній точці
![]() є рівнянням
гіперболічного типу.
є рівнянням
гіперболічного типу.
Якщо при зведенні квадратичної форми (5) до суми квадратів існує більше одного додатного коефіцієнта і більше одного від’ємного коефіцієнта, то рівняння (4) в даній точці є рівнянням ультрагіперболічного типу.
Якщо при зведенні квадратичної форми (5) до суми квадратів один коефіцієнт рівний нулю, а всі решта мають один знак і відмінні від нуля, то рівняння (4) в даній точці є рівнянням параболічного типу.
Якщо при зведенні квадратичної форми (5) до суми квадратів всі коефіцієнти відмінні від нуля і є одного знаку, то рівняння (4) в даній точці є рівнянням еліптичного типу.
Метод характеристик. Розвязок мішаної задачі для рівняння гіперболічного типу. Формула Даламбера. Фізична інтерпретація розвязку.
Загальна схема методу Фурє. Крайова задача Штурма-Ліувіля на знаходження власних значень, власних функцій. Теорема Стеклова.
Поняття потенціалу як безрoзмірної узагальненої величини кількісної взаємодії між обєктами (рівняння Лапласа, Пуассона). Моделювання стаціонарних процесів за допомогою рівнянь еліптичного типу.
Топологічні простори. Підпростір топологічного простору.
Топологія
вивчає властивості геометр. фігур,
інваріантні щодо всіх взаємнооднозначних
і взаємнонеперервних відображень. Якщо,
наприклад, мова іде про поверхню,
реалізовану у вигляді гнучкої і розтяжної
плівки, то її взаємнооднозначними і
взаємнонеперервними перетвореннями
(відображеннями на себе) будуть її розтяг
і стиск без розривів і склеювань.
Фундаментальним поняттям топології є
поняття топологічного простору, який
вводиться таким чином.![]()
Множина
R,
елементи якої наз. точками,
наз. топологічним
простором,
якщо в ній задано сімейство Ф
= {![]() }
її підмножин
,
які наз. відкритими
множинами,
і притому так, що виконуються наступні
аксіоми.
}
її підмножин
,
які наз. відкритими
множинами,
і притому так, що виконуються наступні
аксіоми.
I. Об'єднання будь-якої кількості (скінченної або нескінченної) відкритих множин є відкрита множина.
II. Перетин будь-яких двох відкритих множин є відкрита множина.
ІІІ.
Порожня множина
![]() і вся множина
R
є відкритими множинами.
і вся множина
R
є відкритими множинами.
Вважаємо, що сімейство Ф = { } є топологічною структурою на R, або просто топологією. Таким чином, топологічний простір є пара, яка складається із множини R і введеної на ній топологічної структури Ф. Топологічний простір позначається через (R, Ф) і лише в тих випадках, коли ясно, про яку топологічну структуру Ф йде мова, топологічний простір (R, Ф) позначається просто через R.
З
аксіоми II
![]() ,
що перетин
скінченного числа відкритих множин є
відкрита множина.
,
що перетин
скінченного числа відкритих множин є
відкрита множина.
Приклади топологічних просторів.
1. У довільній нескінченній множині R відкритими множинами вважатимемо тільки дві множини—порожню множину і саму множину R. Така топологія наз. тривіальною.
2. Нехай R—довільна множина. Відкритими множинами вважатимемо всі підмножини множини R, включаючи порожню множину. Така топологія наз. дискретною.
Околом
точки а
топологічного простору R
наз. будь-яку відкриту множину U![]() R,
що містить точку а.
R,
що містить точку а.
Нехай
R —
топологічний простір, а М
— довільна
множина точок цього простору. Т. а![]() М
наз. внутріш.
точкою
множини М,
якщо існує такий окіл U
М
наз. внутріш.
точкою
множини М,
якщо існує такий окіл U![]() точки а,
що U
М.
точки а,
що U
М.
Теорема: Всі точки відкритої множини є внутрішніми точками. Навпаки, якщо всі точки множини F R топологічного простору (R, Ф) внутрішні, то множина F є відкритою. Довед.
1-а
част. Дано: множина відкрита. Довед. що
всі точки внутрішні. Справді, для кожної
точки даної множини існує окіл, який
належить множині
![]() .
Отже, точки внутрішні.
.
Отже, точки внутрішні.
2-а
част. Дано: всі точки множини внутрішні.
Доведемо, що множина відкрита. Оскільки
всі точки множини F
внутрішні,
то для будь-якої точки а
цієї множини існує такий окіл U
,
що U
F. Легко
побачити, що F
=![]() Ua.
Згідно
аксіоми І, F—відкрита
множина.
Ua.
Згідно
аксіоми І, F—відкрита
множина.
Покажемо, що будь-яка підмножина топологічного простору може бути розглянута як топологічний простір. Справді, нехай (R, Ф) топологічний простір, а М підмножина множини R.
Відкритою
множиною в М
наз. будь-яку
її підмножину виду
F'
=М![]() F
,
де F'
–будь-який
елемент сімейства Ф.
Легко
переконатися
в тому, що при цьому означенні виконуються
всі аксіоми I–III топологічного простору,
тому ми говоритимемо, що на множині М
індукується
(породжується) топологічна структура
Ф'={
F'
}.
F
,
де F'
–будь-який
елемент сімейства Ф.
Легко
переконатися
в тому, що при цьому означенні виконуються
всі аксіоми I–III топологічного простору,
тому ми говоритимемо, що на множині М
індукується
(породжується) топологічна структура
Ф'={
F'
}.
Топологічний простір (М,Ф') наз. підпростором топологічного простору (R, Ф).
