2.2. Теплопроводность

При теплопроводности тепловая энергия передается за счет движения и взаимодействия молекул. Интенсивность переноса тепла определяется температурным напором и свойствами тела. Процесс теплопроводности описывается законом Фурье

(2.2)

где  – коэффициент пропорциональности, называемый коэффициентом теплопроводности, Вт/(мК); dF – площадь, нормальная тепловому потоку, м²; d – время, с; dt – перепад температур, С; dn –расстояние между изотермами по нормали, м.

Коэффициент теплопроводности (обычно его называют просто теплопроводностью) является теплофизической константой материала, определяется его природой и зависит от температуры и, в некоторой степени, от давления. Он численно равен количеству тепла, проходящему в теле через площадку в один квадратный метр за одну секунду на расстояние в один метр при перепаде температур в один градус. Наибольшие значения теплопроводности у меди =450 Вт/(мК), затем идут металлы, строительные материалы и неметаллы, жидкости, теплоизоляционные материалы. Самые низкие значения, порядка 0,02 Вт/(мК), характерны для газов. С увеличением температуры теплопроводность обычно снижается. Зависимостью теплопроводности от давления, как правило, пренебрегают. Формулы для приближенного расчета теплопроводности различных веществ приведены в разделе 1 части первой данной книги.

Предел отношения разности температур к расстоянию между изотермами по нормали, представляющий собой производную температуры по нормали, называют температурным градиентом. Так же как и тепловой поток, температурный градиент является векторной величиной с направлением, противоположным тепловому потоку. Знак минус в уравнении Фурье учитывает противоположность направлений векторов теплового потока и температурного градиента.

Процесс нестационарной теплопроводности описывается дифференциальным уравнением теплопроводности, полученным из теплового баланса элементарного параллелепипеда с ребрами dx, dy и dz при условии независимости свойств вещества от координат и температуры. Тепло расходуется на изменение средней температуры вещества во времени t/. Расход тепла dQ определим как произведение массы dm=dV=dxdydz, теплоемкости с, времени d и изменения температуры во времени t/: cdVdt/. Приход тепла складывается из тепла за счет теплопроводности через грани параллелепипеда с площадями dFz=dx dy, dFy=dx dz и dFx=dz dy и внутренних источников тепла qVdV d. Тепло, поступающее за счет теплопроводности, определим по уравнению Фурье, в котором градиент температуры dt/dn представим как произведение частной производной на дифференциал аргумента. Теплопроводный поток составит: для оси z – dF_z d (t/z)/z, для оси у – dF_y d (t/y)/y и оси x – dF_x d (t/z)/z. Приравняв приход тепла расходу, после несложных преобразований получим дифференциальное уравнение нестационарной теплопроводности с внутренними источниками тепла

, или , (2.3)

где а=/(с) – коэффициент температуропроводности (или просто температуропроводность), м²/с; q_V – интенсивность внутренних источников (стоков) тепла, Вт/м³;  – плотность, кг/м³; с – теплоемкость, Дж/(кгК); ²t=²t/x²+²t/у²+²t/z² – оператор Лапласа по температуре.

Решение дифференциального уравнения возможно только при использовании условий однозначности, т.е. в общем виде невозможно.

Для стационарных условий (t/=0) и одномерного температурного поля (неограниченная пластина с тепловым потоком, направленным по нормали к поверхности t/у=0 и t/z=0) при отсутствии внутренних источников (qV=0) уравнение (2.3) примет вид d2t/dx2=0.

Интегрирование последнего уравнения приводит к выражениям dt/dx=C₁ и t=C₁x+C₂. Как видно из последних выражений, температура по толщине неограниченной пластины изменяется по линейной зависимости. Константы интегрирования С₁ и С₂ определим подстановкой граничных условий. При х=0 температура на поверхности равна t_cт¹. На противоположной поверхности при х= температура равна t_cт². После подстановки получаем C₁=(t_cт²-t_cт¹)/ и C₂=0. Подставляя значение производной dt/dx=(t_cт²-t_cт¹)/ в уравнение Фурье (2.2), получим уравнение теплопроводности плоской неограниченной пластины тепла для стационарных условий

q=Q/(F)=t/=t/R, (2.4)

где t=t_ст¹-t_ст² – температурный напор теплопроводности, С; t_ст¹,t_ст² – температуры наружных поверхностей стенки, С;  – толщина стенки, м;  – время, с; R=/ – термическое сопротивление плоской стенки, м²К/Вт.

Для расчета многослойных плоских стенок используют уравнение (2.4), но термическое сопротивление определяется как сумма сопротивлений слоев

R=_i/ _i . (2.5)

Как уже отмечалось, температура в плоской стенке изменяется по линейной зависимости (прямая 2 на рис.2.1,а), что справедливо при отсутствии зависимости теплопроводности от температуры и координат. Для возрастающей зависимости теплопроводности от температуры распределение температур будет криволинейным с более пологой частью в области высоких температур (кривая 1 на рис.2.1,а). Для большинства веществ с ростом температуры теплопроводность снижается, и для реальных тел кривая распределения температур выполаживается в области низких температур (кривая 3 на рис.2.1,а).

Д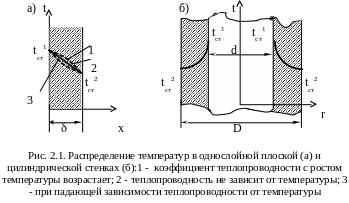 ля цилиндрических стенок распределение температур подчиняется логарифмической зависимости и расчетное уравнение, получаемое интегрированием закона Фурье, для бесконечной цилиндрической стенки имеет вид

Q= и q_L= , (2.6)

где L – длина стенки, м; R_L= – линейное термическое сопротивление, мК/Вт.

Для многослойной цилиндрической стенки линейное термическое сопротивление определяется суммированием линейных термических сопротивлений слоев

R_L= . (2.7)

Для снижения потерь тепла трубопроводами в окружающую среду их покрывают слоем теплоизоляции. В этом случае тепло от горячего теплоносителя Q₁=₁(t₁-t_ст)F₁ конвекцией отдаётся стенке трубопровода, затем путем теплопроводности многослойной стенки (труба+изоляция) проходит к наружной поверхности Q_ст=L(t_ст1– –t_из)/[ln(d_в/d_н)/(2_cт)+ln(d_н/d_из)/(2_из)] и от нее конвективным путем отдается в окружающую среду Q₂=₂(t_из-t₂)F₂. При стационарных условиях все три тепловых потока одинаковы, т.е. Q₁=Q_cт=Q₂=Q. Выделим из выражений тепловых потоков разности температур, проведем сложение правых и левых частей равенств. Учитывая, что F₁=d_вL, F₂=d_изL и Q₁=Q_cт=Q₂=Q, получим

Q=L(t₁-t₂)/[1/(₁d_в)+ln(d_в/d_н)/(2_cт)+ln(d_н/d_из)/(2_из)+1/(₂d_из)], (2.8)

где ₁ и ₂ – коэффициенты теплоотдачи, Вт/(м²К).

Почти во всех реальных случаях первые два слагаемых знаменателя 1/(₁d_в) и ln(d_в/d_н)/(2_cт) пренебрежительно малы. Тогда q_L=Q/L=(t₁–t₂)/[ln(d_н/d_из)/(2_из)+1/(₂d_из)]. С увеличением диаметра изоляции d_из первый член суммы в знаменателе растет, а второй – уменьшается. Следовательно, зависимость q_L=f(d_из) при d(q_L)/d(d_из)=0 будет иметь минимальную точку. После дифференцирования и приравнивания производной нулю, получим выражение для критического значения диаметра изоляции, соответствующего максимуму передаваемого тепла:

d_кр=2_из/₂. (2.9)

Если диаметр трубопровода будет превышать критический диаметр, то использование теплоизоляции однозначно будет снижать тепловые потери. В противном случае, т.е. при d_н<d_кр, использование теплоизоляции с толщиной до (d_кр-d_н)/2 тепловые потери будет увеличивать, а при дальнейшем увеличении толщины теплоизоляции теплопотери будут вновь снижаться.

К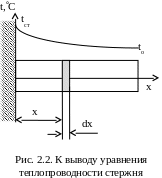 оэффициент теплоотдачи к воздуху 10 Вт/(м²К), теплопроводность многих теплоизоляционных материалов 0,1 Вт/(мК). Для этих условий d_кр=20,1/10=0,02 м=20 мм, и для теплоизоляции труб с диаметром порядка 20 мм использование материалов с коэффициентом теплопроводности около 0,1 Вт/(мК) будет неэффективным. Для этих целей необходимо использовать материалы с меньшей теплопроводностью, например, стекловату с теплопроводностью 0,050,08 Вт/(мК).

В ряде случаев теплообменные поверхности промышленных аппаратов увеличивают использованием оребрения. Рассмотрим стационарную теплопроводность стержня длиной L, находящегося в среде с постоянной температурой и заделанного одним концом в стенку с постоянной температурой (рис.2.2). Будем полагать, что стержень имеет достаточно большую длину и его температура на конце равна температуре окружающей среды. Тепло от горячей стенки будет распространяться по стержню за счет его теплопроводности. В процессе прохождения тепла по стержню часть его будет отводиться в окружающую среду за счет конвекции. В соответствии с этим средняя температура стержня будет изменяться от максимальной в месте его заделки до минимальной и равной окружающей среде на достаточно большом удалении от стенки. Рассмотрим тепловой баланс элементарного слоя стержня толщиной dx на расстоянии х от места заделки стержня. Обозначим периметр стержня П и его сечение S. Тогда поверхность выделенного объема определится по формуле dF=П dx. Тепло, входящее в выделенный объем слева, определим по уравнению Фурье Q_x=- S(dt/dx). За счет конвекции часть этого тепла dQ=(t-t_c)dF=(t-t_c)П dх отведется в среду, а остальное пройдет дальше по стержню за счет теплопроводности Q_x+dx=-S(dt/dx)-(Q/x)dx. Приравняв разность теплопроводных потоков тепла конвективному тепловому потоку и произведя сокращения, получим ₁=(t_ст–t₀)П=-(Q/x)=S(²t/x²).

Заменив температуру t на относительную v=t_ст-t₀ и обозначив комплекс констант для конкретного стержня одной величиной m=[П/(S)]^0,5, получим

²v/x²=mv. (2.10)

Решение последнего дифференциального уравнения второго порядка имеет вид

v=C₁exp(mx)+C₂exp(-mx).

Константы интегрирования этого решения определим из граничных условий:

– при х=0  v=v_o и С₁+С₂=v_o;

– при х=L  v=0 и C₁exp(Lm)+C₂exp(-Lm)=0.

C₁=v_oexp(mL)/[exp(-mL)+exp(mL)]

и C₂=v_oexp(mL)/[exp(-mL)+exp(mL)].

Подставив значение констант интегрирования в решение дифференциального уравнения, получим

v=v_o{exp[m(x-L)]+exp[-m(x-L)]}/[exp(-mL)+exp(mL)]= =v_och[m(x-L)]/ch(mL), (2.11)

где ch[m(x-L)] – гиперболический косинус произведения m(x-L).

Для конца стержня x=L выражение (2.9) упрощается:

v=v_o/ch(mL). (2.12)

Количество тепла, отведенное от поверхности стержня, при стационарных условиях будет равно теплу, входящему в стержень в месте его заделки Q=-S(dv/dx)_x=0. Производную (dv/dx)_х=0 определим дифференцированием решения уравнения (2.9). После подстановки производной и констант интегрирования в последнее выражение, получим

Q=mSv_o[exp(mL)-exp(-mL)]/[exp(-mL)+exp(mL)]=mSv_oth(mL),(2.13)

где th(mL)=[exp(mL)-exp(-mL)]/[exp(-mL)+exp(mL)] – гиперболический тангенс произведения mL.

Анализ выражения (2.13) показывает, что увеличение длины стержня ведет к увеличению количества отводимого тепла. При этом следует отметить, что рост mL свыше 23 тепловой поток практически не изменяет.

П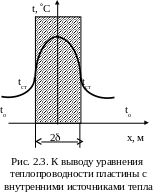 ри использовании электронагрева мы имеем дело со стационарной теплопроводностью с внутренними источниками тепла. Рассмотрим бесконечно большую пластину (рис.2.3) с равномерно распределенными по её объему постоянно действующими источниками тепла интенсивностью q_v (Вт/м³). Так как условия теплообмена с обеих сторон стенки одинаковы, то температурное поле можно считать симметричным и имеющим максимум на оси пластины. Таким образом, при х=0 градиент температуры dt/dx=0. На поверхности пластины (х=) тепловой поток со стороны пластины, определяемый по уравнению Фурье q=-dt/dx, равен теплу, отводимому от стенки конвекцией q=(t_cт-t_o). Таким образом, на поверхности стенки при х=  -dt/dx=(t_cт–t_o) и -dt/dx=(t_cт–t_o)/.

Дифференциальное уравнение нестационарной теплопроводности для плоской пластины при стационарных условиях с внутренними источниками тепла будет иметь вид d²t/dx²+q_v/=0. Интегрируя это уравнение, получим dt/dx=-хq_v/+С1 и t=-x²q_v/(2)+С₁х+C₂.

Константы интегрирования определим из граничных условий:

– при х=0  dt/dx=0; dt/dx=-хq_v/+С₁=0 и С₁=0;

– при х=  dt/dx=- (t_cт-t_o)/ и dt/dx=-хq_v/+С₁=-q_v/+0.

Приравняв правые и левые части последних двух равенств, имеем – хq_v/=–(t_cт–to)/. Отсюда t_cт=t_o+q_v/.

На поверхности пластины (при х=) температура в соответствии с решением дифференциального уравнения определится выражением t=t_cт=-х²q_v/(2)+С₁х+C₂. Подставляя в последнее выражение х=; С₁=0 и t_cт=t_o+q_v/, получим выражение для константы интегрирования С₂=t_o+q_v/+²q_v/(2). Окончательно для температуры в произвольном сечении стенки имеем

t=t_o+q_v/+(²-x²)q_v/(2). (2.14)

Судя по уравнению (2.13), температура в пластине изменяется по параболе с максимумом на её оси, определяемым по формуле

t_ц=t_o+q_v/+²q_v/(2). (2.15)

При стационарной теплопроводности бесконечного стержня с внутренними источниками тепла температура определяется также квадратичными уравнениями:

t=t_o+[1-(r/R)²]q_vR²/(4)+q_vR/(2) и t_ц=t_o+R²q_v /(4)+q_vR/(2), (2.16)

где R – радиус стержня, м.