
тервер решения к методичке
.pdf
Контрольные задачи к разделу 1
1.1. В лотерее 10 билетов, из которых 4 выигрышных. Какова вероятность выиграть, имея 3 билета?
Решение:
вероятность выиграть, имея три билета, состоит в наступлении хотя бы одного из трех событий, которые являются совместными. В этом случае вместо формулы суммы вероятностей удобнее использовать формулу вычисления вероятностей произведения противоположных событий:
|
|
|
. |
Вероятность |
наступления каждого |
из событий |
вычисляется по |
формуле классического определения вероятности: |
|
||
|
|
. |
|
где - число возможных исходов, а |
- число благоприятных исходов. |
||
|
|
|
. |
Ответ: |
. |
|
|
1.2. Телефонный номер состоит из пяти цифр. Найти вероятность того, что все цифры различны.
Решение:
первая цифра может быть любой. Вероятность того, что вторая отличается от первой 9/10, третья отличается от предыдущих 8/10, четвертая и пятая от предыдущих 7/10 и 6/10 соответственно.
Вероятность всех различных 1*9/10*8/10*7/10*6/10=0.3024. Ответ: 0.3024
1.3. Какова вероятность вытащить 2 разноцветных шара из ящика, где 8 белых и 12 черных.
Решение:
существует два варианта выбора разноцветных шара: сначала вытащить черный шар, а затем белый, или сначала вытащить белый шар, а затем черный.
12
Вероятность вытащить первым черный шар равна 8 +12 , а затем вторым
белый |
|
|
12 |
|
× |
|
|
8 |
|
= |
|
48 |
. Вероятность вытащить первым белый шар |
|||||||||
8 |
+12 |
8 |
+12 -1 |
190 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
равна |
|
|
8 |
|
, а |
|
затем |
вторым |
черный |
|
8 |
× |
12 |
= |
|
48 |
. Итоговая |
|||||
8 |
+12 |
|
|
8 |
+12 |
8 +12 -1 |
190 |
|||||||||||||||
|
|
|
|
|
45 . |
|
|
|
|
|
|
|
|
|||||||||
вероятность равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
95 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45
Ответ: 95 .
1.4. У первого акционера 9 акций вида А и 12 акций вида В. У второго, соотвественно, 5 и 9. В результате операции купли-продажи 7 акций первого перешли ко второму держателю акций. Найти вероятность того, что случайно выбранная акция второго акционера окажется вида А.
Решение:
рассмотрим гипотезы: Н1 — взятая акция была из 7 купленных у первого, Н2 — взятая акция первоначально была у второго.
Тогда |
P (H 1)= |
|
7 |
|
= |
1 |
, P (H 2)= |
5+ 9 |
= |
2 |
. Пусть А — событие, когда взятая |
||||||||||||
7+ |
5+ 9 |
3 |
7+ 5+ 9 |
3 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
акция |
|
вида |
|
А, |
|
тогда |
|
|
по |
|
|
формуле |
|
полной |
вероятности: |
||||||||
P (A)=P (H 1) P ( A H 1)+ P( H 2) P (A H 2) . |
|
|
|
|
|
|
|
|
|
||||||||||||||
P (A H 1)= |
9 |
|
=3 |
, P ( A H 2 )= |
5 |
= |
5 |
, тогда |
P (A)= 1 + |
5 |
= |
8 |
≈0,38 |
. |
|||||||||
12+ 9 |
|
5+ 9 |
|
21 |
|
||||||||||||||||||
|
|
|
7 |
|
|
|
|
|
|
14 |
7 |
21 |
|
||||||||||
Ответ: P ( A)=0,38 .
1.5. Устройство состоит из 12 независимых блоков, помеченных Б1, Б2, …, Б12. Вероятность того, что неисправность может произойти в одном из блоков Б1, Б2, БЗ, Б4 составляет 0,6. При поиске появившейся неисправности обследованы блоки Б1, Б2, БЗ, но неисправность не обнаружена. Какова вероятность того, что неисправность будет обнаружена в блоке Б4?
Решение:
1.6. Определить вероятность того, что трехзначный номер первой встретившейся автомашины не содержит одинаковых цифр и цифры шесть.
Решение:
воспользуемся формулой: P = mn .
n=103 -все возможные номера;
m = m1 − m2; где:
m1 =93 -все номера без цифры ;
m2 = 3×9 ×C91 , где C91 -выбор только одной цифры;
P = |
m |
= |
m - m |
= |
93 - 3×9×C 1 |
= 0,504. |
|
|
1 2 |
9 |
|||||
n |
n |
||||||
|
|
|
1000 |
|
|||
Ответ: |
Р=0,504 . |
|
|
|
|||
1.7. Из чисел 1, 2, 3, 15 одно за другим выбирают наугад два числа. Какова вероятность того, что разность между первым выбранным числом и вторым числом будет не меньше числа 3?
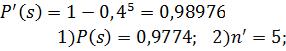
Решение:
1.8. Стержень разламывается на две части в случайной точке, равномерно распределенной по всей длине стержня. Найти вероятность того, что меньший обломок имеет длину, не превосходящую одной трети длины стержня.
Решение:
вероятность, что меньший обломок имеет длину не больше 13 стержня, равна
23 .
Ответ: P= 23
1.9. Для повышения надежности прибора он дублируется тремя такими же приборами. Надежность каждого прибора равна 0.6. Найти надежность системы
. Сколько надо взять приборов , чтобы надежность системы стала 98% ? Решение:
1)n=3, p=0.6, P(s)=?;
2)p’=0.6; P’(s)>0.98; n’=?;
Так как вероятности выхода из строя любого из приборов равны и приборы работают независимо друг от друга, то мы можем найти вероятность того, что все приборы будут неисправны(это единственный случай , когда система неисправна) , и , вычитая из единицы данное решение мы найдем надежность системы.
1)P(s)=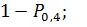
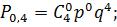 P(s)=
P(s)=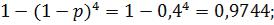
2)P(s)<P’(s) (0,9774<0,98) значит, n’>4, но при n=5:
Значит, n’=5;
Ответ:
1.10. Из колоды в 32 карты берутся 4. Найти вероятность того, что среди них окажется хотя бы одна дама.
Решение:
А- вероятность того, что будет хотя бы одна дама.
Всего 32 карты, из них 4 дамы. При вытягивании первой карты вероятность
того, что не будет дамы Р(А1 ) = 28 = |
7 |
. При вытягивании второй карты |
Р(А2 ) = |
27 . |
|||||||
32 |
8 |
|
|
|
|
|
|
|
|
|
31 |
Третьей Р(А3 ) = 26 . Четвертой Р(А4 ) = |
25 . |
|
|
|
|
|
|
|
|
|
|
30 |
|
29 |
|
|
|
|
7g27g26g25 |
|
|
||
|
|
|
Р( |
|
) = |
= 0.569 |
|
||||
Вероятность того, что среди вытянутых карт нет дам: |
А |
|
|||||||||
|
|
|
|
8 31 30 29 |
|
|
|||||
|
|
|
P(AР) =А1− ( |
|
) = 0.431 |
|
|||||
|
|
|
|
|
|||||||
Вероятность того, что будет хотя бы одна дама: P(AР) =А1− ( |
|
) = 0.431 |
|
|
|||||||
|
|
|
|||||||||
Ответ: Р=0,431 |
|
|
|
|
|
|
|
|
|
|
|
1.11. При переливании крови надо учитывать группы крови донора и больного.

Человеку, имеющему четвертую группу крови, можно перелить кровь любой группы; человеку со второй или третьей группой крови можно перелить кровь либо той же группы, либо первой; человеку с первой группой крови можно перелить только кровь первой группы. Среди населения 30,7% имеют первую, 39,5% - вторую, 21,9% - третью и 7,9% - четвертую группы крови. Найти вероятность того, что случайно взятому больному можно перелить кровь случайно взятого донора.
|
Решение: |
вероятность события |
, заключающегося в том, что случайно взятому |
больному подойдет кровь случайно взятого донора, будем искать по формуле полной вероятности:
|
. |
где |
– вероятность гипотезы ; |
- условная вероятность наступления события 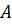 при гипотезе
при гипотезе 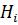 . Вероятности гипотез равны:
. Вероятности гипотез равны:
.
.
Найдем условные вероятности:
1)Если первая группа, то 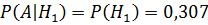 .
.
2)Если вторая группа, то
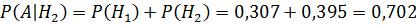 .
.
3)Если третья группа, то
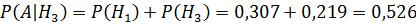 .
.
4)Если четвертая группа, то
.
Тогда вероятность наступления события :
.
Ответ: .
1.12. Какова вероятность, что при игре в преферанс (32 карты раздаются трём игрокам) в прикупе окажутся два туза?
Решение:
для первой карты прикупа допустимо 4 варианта (любой из тузов), всего карт 32, для второй – 3 (из 31) карты, поэтому
Ответ: Р=0.012
1.13. Брошены 3 игральные кости. Найти вероятность того, что в сумме выпало 4.
Решение:
всего исходов 63 = 216 , а благоприятных 3: (1,1,2), (1,2,1), (2,1,1). Итоговая

1
вероятность равна 72 .
1
Ответ: 72 .
1.14. 4 поздравительные открытки случайно разложены по 4-ём конвертам с адресами. Найти вероятность того, что хотя бы одна открытка попала в свой конверт.
Решение:
пусть Аi — событие, когда открытка оказалась в своём конверте. Тогда согласно формуле вероятности суммы событий получим:
4
P (∑ Ai )= A1+ A2+ A3+ A4− A1 A2− A2 A3− A3 A4 −A1 A3−A2 A4−A1 A4+ A1 A2 A3+ A1 A3 A4 ,
i=1
+ A2 A3 A4+ A1 A2 A4−A1 A2 A3 A4
|
P (Ai )= |
1 |
, P ( Ai A j )= |
1 1 |
= |
1 |
, P ( Ai A j Ak )= |
1 1 |
1 |
= |
1 |
, P (A1 A2 |
A3 |
A4)= |
1 |
1 1 1 |
= |
1 |
|
|
где |
4 |
4 3 |
12 |
4 3 2 |
24 |
4 3 2 1 |
24 . |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
P (∑ Ai )= 5 =0,625 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
i=1 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: P (∑ Ai )=0,625 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
i=1
1.15. Из десяти билетов выигрышными являются два. Определить вероятность того, что среди взятых наудачу пяти билетов один выигрышный.
Решение: вероятность выигрыша p= 102 =0.2 . По формуле Бернулли
P1,5=C15 p q4 = 54!! 0.2 0.84 =0.41 .
Ответ: P=0.41
1.16. Устройство состоит из 5 элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что оба элемента будут не изношены.
Решение:
m – включенные устройства не изношены, n – возможность включить два устройства
P = |
m |
= |
C 2 |
= 0.3 |
|
|
3 |
||||
n |
C52 |
||||
|
|
|
Ответ: P=0.3
1.17. Набирая номер телефона, абонент забыл последние три цифры и помня лишь что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Решение:

всего мы имеем десять цифр и нам нужно выбрать три из них, зная лишь что они должны быть различны. Первое число мы можем выбирать из всех десяти, но подойдет нам только одно, второе число мы выбираем уже из девяти чисел, а третье из восьми, поскольку мы знаем что числа не должны повторяться.
Ответ: Р=0,14%.
1.18. Два игрока по очереди бросают игральную кость. Каждый по одному разу. Выигравшим считается тот, кто получит большее число очков. Найти вероятность выигрыша первого игрока.
Решение:
всего может выпасть 36 вариантов, первый игрок выиграет при 15 исходах.
P m 15
Тогда . = n = 36 Ответ: P= 1536
1.19. В коробке 5 одинаковых изделий, 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди 2-х извлеченных изделий окажется одно окрашенное.
Решение: рассмотрим 2 возможных варианта:
1)Р(А) - 1-ый шар окрашенный, Р(В|А) - 2-ой неокрашенный. 2)Р(В) - 1-ый шар неокрашенный, Р(А|В) - 2-ой окрашенный.
Тогда по формуле 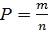 получим: 1)
получим: 1)
2)
Сложим найденные результаты и получим Р=0,6 Ответ: Р=0,6
1.20. Среди 10 электрических лампочек три нестандартные. Найти вероятность того, что две одновременно лампочки окажутся нестандартными.
Решение:
А1 - вероятность получения одной нестандартной лампочки. А2вероятность получения второй нестандартной лампочки.
А - вероятность того, что две одновременно лампочки окажутся нестандартными.
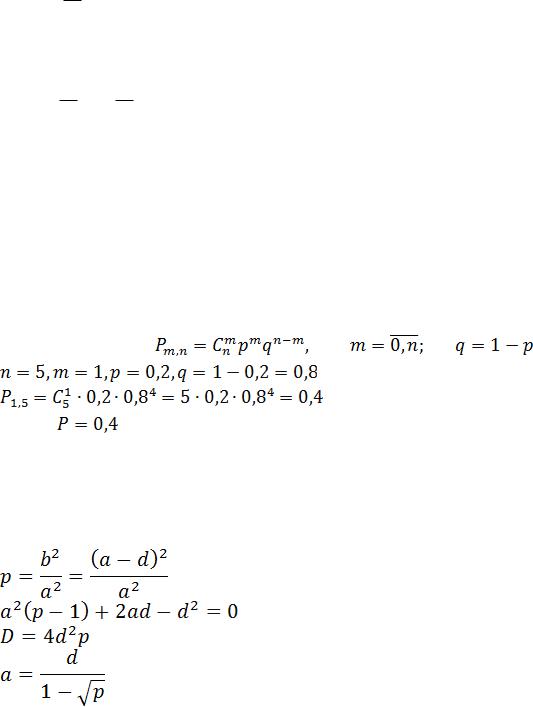
Р(А1) = 103 Р(А2 ) = 92
Р(А) = 103 g92 = 151 = 0.066 Ответ: Р=0,066 .
1.21. Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Найти вероятность того, что из пяти первых покупателей обувь этого размера будет необходима одному.
Решение:
в данном случае производится 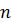 независимых опытов в одинаковых условиях, причем в каждом из них с вероятностью
независимых опытов в одинаковых условиях, причем в каждом из них с вероятностью 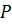 может появиться событие
может появиться событие 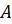 , поэтому применим формулу Бернулли:
, поэтому применим формулу Бернулли:
.
.
.
Ответ: .
1.22. Вероятность того, что монета диаметром d не пересечёт ни одну сторону квадратной сетки равно p. Определить размер сетки.
Решение:
a=b+d, b=a-d
1.23. Два корабля должны подойти к одному и тому же причалу. Время прихода обоих кораблей независимо и равновозможно в течение суток. Определить вероятность того, что одному кораблю придется ожидать освобождения причала, если время стоянки первого корабля составляет два часа, а второго – три часа.
Решение:
пусть у – время прихода второго корабля, а х – первого. Тогда, условие не
ìy > x + 2 |
ìy > x + 2 |
. Тогда искомая |
ожидания будут выглядеть так: í |
, или í |
|
îx > y + 3 |
îy < x - 3 |
|
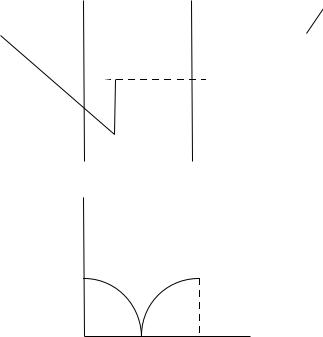
вероятность равна |
1- |
222 + 212 |
= |
227 |
» 0,197 |
. |
2 × 242 |
1152 |
|||||
|
|
|
|
|
Ответ: 0,197 .
1.24. На обслуживающее устройство в промежуток времени [0,12] должны поступить 2 заявки. Если разность между моментами поступления заявок меньше 2, то вторая заявка теряется. Найти вероятность потери заявки.
Решение:
заявки х и у могут поступить в промежуток [0,12] не зависимо друг от друга. Событие А — потеря заявки происходит, когда x− y < 12 . Рассмотрим график этой функции. Тогда по геометрической интерпретации задачи
P (A)= |
S x− y < 12 |
. |
|
|
|
S 0< x< 12,0< y< 12 |
|
|
|
||
|
|
|
|
|
|
S x− y < 12=122−102=44, |
S 0< x< 12,0< y< 12=122 =144, |
. |
|||
|
P ( A)= |
44 |
≈0,3 |
||
|
144 |
|
|||
|
|
|
|
|
|
Ответ: P (A)=0,3
1.25. Найти вероятность того, что сумма двух случайных чисел из отрезка [- 1, 2] больше единицы, а их произведение меньше единицы.
Решение:
1.26. На пол, разграфленный параллельными прямыми на полосы шириной а, бросается наугад игла длины l (l<a). Найти вероятность того, что иголка пересечет какую-либо прямую.
Решение:
|
|
y |
|
L |
||
L |
cosα = |
|
|
Þ y = |
|
cosα |
L |
2 |
2 |
||||
|
|
|
|
|
|
|
α
L/2
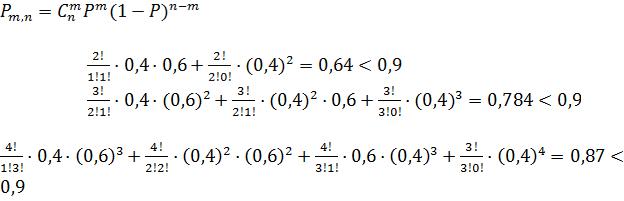
0 |
|
|
|
|
pi/2 |
pi |
|||
|
|
π |
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
L |
|
S1 = |
ò0 |
|
|
|
cosαdα = |
|
|
||
|
2 |
2 |
|||||||
|
|
|
|
|
|||||
S = |
|
L |
* 2 = L |
|
|
||||
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
P = |
2L |
|
|
|
|
|
|||
aπ |
2L |
|
|
|
|||||
|
|
|
|
||||||
Ответ: P = |
|
|
|||||||
α α |
|
|
|||||||
1.27. На плоскости отрезок длиной 10 см закреплен в одним концом и вращается вокруг точки закрепления так, что все направления отрезка равновероятны. Найти среднюю проекцию отрезка на заданную ось.
Решение:
1.28. Стрельба заканчивается после третьего попадания по мишени. Найти вероятность того, что при этом будет 5 промахов, если вероятность попадания при одном выстреле равна 0,3.
|
|
Решение: |
|
|
||||
по формуле Бернулли |
P3,8=C53+ 3 |
p3 q5= |
8 ! |
|
0.33 0.7 |
5=0.25 |
. |
|
3! 5 |
! |
|||||||
|
|
|
|
|||||
Ответ: P=0.25
1.29. Вероятность того, что посетитель страховой компании заключит с ней какой-либо договор, равна 0,4. Сколько посетителей надо обслужить, чтобы с вероятностью не меньшей, чем 0,9 можно было утверждать, что будет заключен договор?
Решение:
т.к. производится n одинаковых опытов(в одинаковых условиях) и вероятность появления события А в каждом опыте одна и та же( Р=0.4), т о вероятность события А вычисляется по формуле Бернулли:
1 |
клиент: 0,4<0,9 |
2 |
клиента: |
3 |
клиента: |
4 |
клиента: |
5 |
клиентов: |

Ответ: 5
1.30. Производится залп из 6 орудий по некоторому объекту. Вероятность попадания в объект из каждого орудия равно 0.6. найти вероятность ликвидации
объекта, если для этого необходимо не менее 4 попаданий. |
|
|
|
|||||||
|
|
|
|
Решение: |
|
|
|
|
|
|
Р=0,6 |
– вероятность |
попадания |
в |
объект |
из |
каждого |
орудия, |
|||
q = 1− p = 1− 0,6= 0,4. |
|
|
|
|
|
|
|
|
||
А- |
поражение |
цели. |
Воспользуемся |
формулой |
Бернулли: |
|||||
Pm,n = Cnm Pm ( 1− P) n−m ; |
Мы |
можем |
ее |
использовать, |
так |
как |
имеем |
|||
многократное повторение опыта в задаче.
Р4,6 = С64 gР4 gq2 Р5,6 = С65 gР5 gq
Р6,6 = С66 gР6 gq0
P(4 ≤ AР≤ 6) =Р 4,6 +Р 5,6 + 6,6 = 0.5442
Ответ: Р=0,5442 .
1.31. Вероятность хотя бы одного попадания стрелком в мишень при трех выстрелах равна 0,875. Найти вероятность попадания при одном выстреле.
Решение:
вероятность хотя бы одного появления события 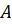 в
в  независимых опытах в одинаковых условиях выражается формулой:
независимых опытах в одинаковых условиях выражается формулой:
.
.
Ответ: .
1.32.Сотрудники отдела маркетинга предполагают, что в ближайшее время ожидается рост спроса на продукцию фирмы. Вероятность этого они оценивают в 80%. Консультационная фирма, занимающаяся прогнозом рыночной ситуации, подтвердила предположение о росте спроса. Положительные прогнозы консультационной фирмы сбываются с вероятностью 95%, а отрицательные – с вероятностью 99%. Какова вероятность, что рост спроса действительно произойдёт?
Решение: решим задачу по формуле полной вероятности:
2
Р(А) = åР(Нi ) × P(A / Hi ), где H1 – спрос вырастет; H2 – спрос понизится; A/H1 –
i=1
прогноз оправдается; A/H2 – прогноз не оправдается;
