
- •Е.Г. Романова Дифференциальная геометрия
- •Содержание
- •1. Векторная функция скалярного аргумента
- •1.1. Определение вектор-функции. Предел. Непрерывность
- •1.2. Дифференцирование вектор-функции
- •1.3. Интеграл от векторной функции по скалярному аргументу
- •2. Сведения из теории кривых
- •2.1. Элементарная кривая
- •2.2. Касательная прямая к кривой
- •2.3. Соприкасающаяся плоскость кривой
- •2.4. Длина дуги как параметр
- •2.5. Кривизна кривой
- •2.6. Кручение кривой
- •2.7. Формулы Френе
- •3. Теория поверхностей в дифференциальной геометрии
- •3.1. Элементарная поверхность
- •3.2. Регулярная поверхность
- •3.3. Кривые на поверхности
- •3.4. Касательная плоскость и нормаль к поверхности
- •3.5. Измерение на поверхности длин, углов, площадей. Первая квадратичная форма поверхности
- •3.6. Площадь поверхности
- •3.7. Вторая квадратичная форма поверхности
- •3.8. Кривизна кривой, лежащей на поверхности
- •3.9. Главные направления и кривизны поверхности
- •3.10. Внутренняя геометрия поверхности
- •Литература:
3.7. Вторая квадратичная форма поверхности
Вторая квадратичная форма описывает поверхность во втором приближении. Она показывает, как отклоняется поверхность от касательной плоскости и полностью определяет кривизну поверхности. Можно было бы само понятие второй квадратичной формы ввести, исходя из задачи о вычислении расстояния от точки поверхности до касательной плоскости, проведенной через близкую точку.
Пусть f – регулярная поверхность, заданная уравнением , а
– линия на этой
поверхности. Имеем
![]() .
Введём вектор нормали
.
Введём вектор нормали
![]() ,
тогда единичный вектор нормали в точке
M
к поверхности f
имеет вид
,
тогда единичный вектор нормали в точке
M
к поверхности f
имеет вид
![]() .
Найдём квадратичную форму
.
Найдём квадратичную форму
![]() .
Так как
.
Так как
![]() ,
то скалярное произведение
,
то скалярное произведение
![]() и, следовательно,
и, следовательно,
![]() .
.
Отсюда
(3.11)
![]()
Здесь учтено, что
![]() ,
,
![]() ,
т.е. отсутствуют слагаемые с этими
произведениями.
,
т.е. отсутствуют слагаемые с этими
произведениями.
Введём
обозначения
![]()
или в координатах:
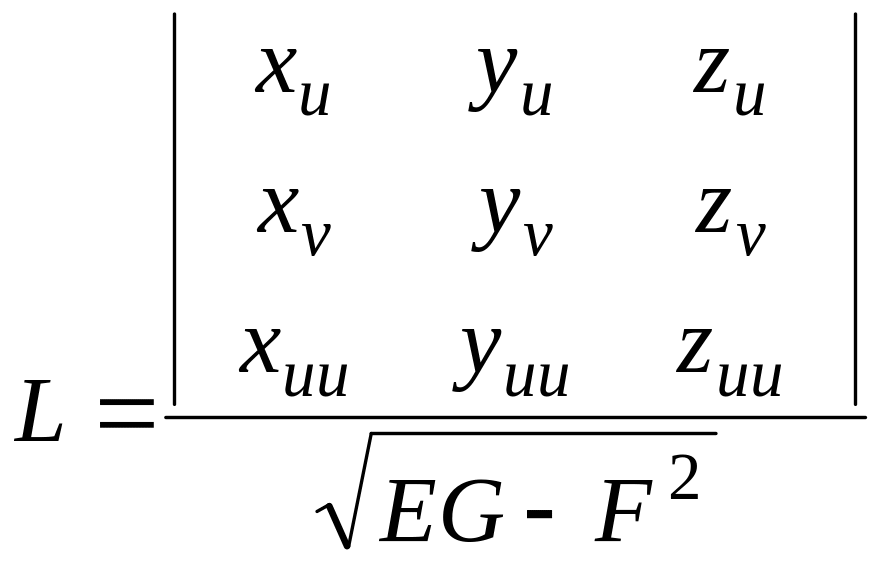 и аналогично,
и аналогично,
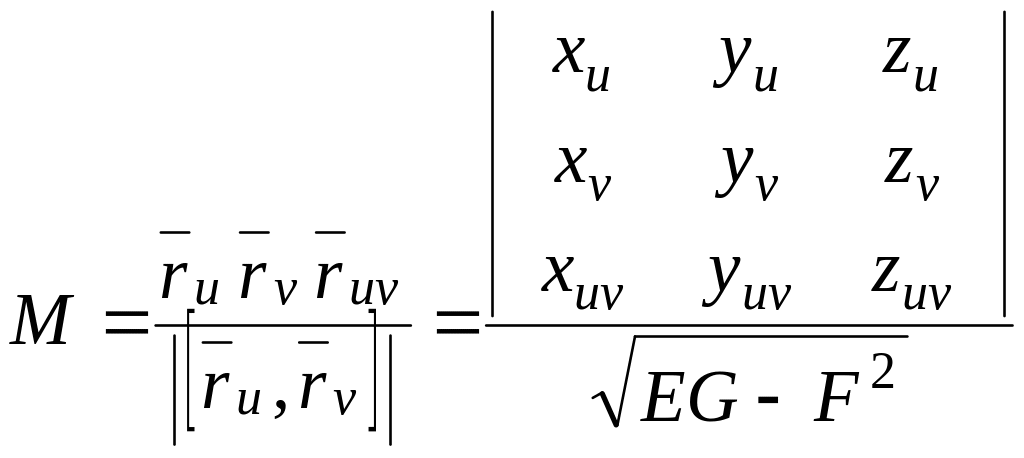 ,
,
![]()
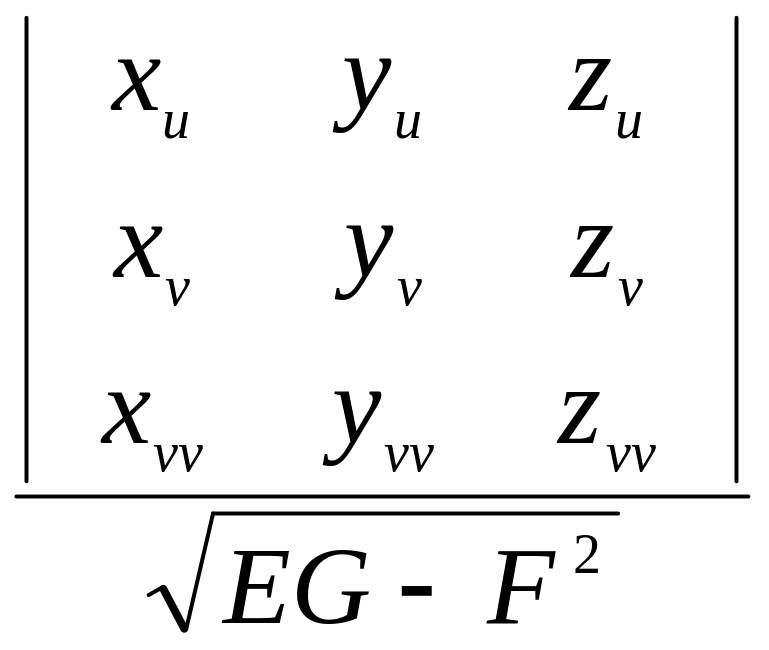 .
.
Замечание
3.3.
Здесь
![]() – дифференциал второго порядка и
– дифференциал второго порядка и
![]() – квадрат дифференциала.
– квадрат дифференциала.
Т
(3.12)
![]() .
.
В формуле (3.12) правая часть равенства называется второй квадратичной формой поверхности.
Замечание
3.4.
В частности,
если поверхность задана явным уравнением
![]() ,
то
,
то
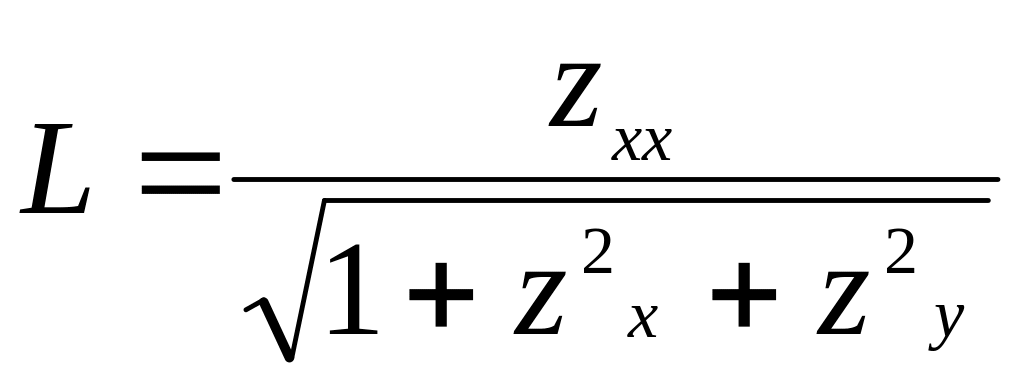 ,
,
 ,
,
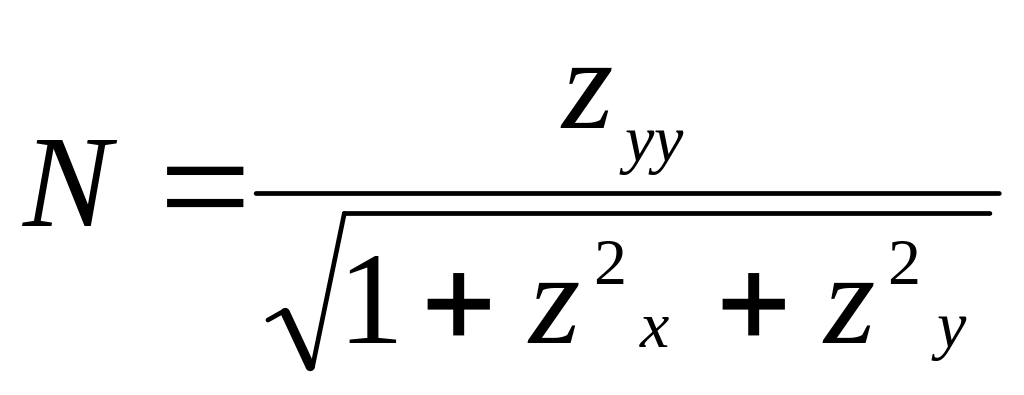 .
.
3.8. Кривизна кривой, лежащей на поверхности
Пусть f – регулярная поверхность и – регулярная кривая на поверхности f, проходящая через точку M.
Предположим,
что вдоль этой кривой за параметр принята
длина дуги s,
так что текущие координаты u
и v
выражаются
как функции от s
(естественная параметризация кривой):
u=u(s),
v=v(s)
и, следовательно, кривая
может быть представлена в виде
![]() .
.
Рассмотрим
скалярное произведение
![]() ,
где
,
где
![]() и
и
![]() -
единичный вектор нормали к поверхности.
Тогда
-
единичный вектор нормали к поверхности.
Тогда
![]() ,
где
,
где
![]() есть угол между главной нормалью
есть угол между главной нормалью
![]() кривой и нормалью
кривой и нормалью
![]() к поверхности.
к поверхности.
Так как
![]() ,
где k
– кривизна кривой, то имеем
,
где k
– кривизна кривой, то имеем
![]() .
С другой стороны, учитывая, что
.
С другой стороны, учитывая, что
![]() имеем
имеем
![]()
=![]()
![]()
=![]() .
.
Следовательно,
учитывая, что
![]() ,
имеем
,
имеем
![]() .
.
Правая часть
этого равенства зависит только от
направления кривой в точке M(u,
v).
Таким образом,
![]() в точке M(u,
v)
для всех
кривых
,
проходящих через эту точку и имеющую в
ней одну и ту же касательную плоскость.
в точке M(u,
v)
для всех
кривых
,
проходящих через эту точку и имеющую в
ней одну и ту же касательную плоскость.
Величину
![]() называют нормальной
кривизной
линии
в точке M.
Если
–
нормальное
сечение
поверхности, т.е. сечение поверхности
плоскостью, проходящей через нормаль
к поверхности в точке M,
то тогда справедлива следующая теорема.
называют нормальной
кривизной
линии
в точке M.
Если
–
нормальное
сечение
поверхности, т.е. сечение поверхности
плоскостью, проходящей через нормаль
к поверхности в точке M,
то тогда справедлива следующая теорема.
Теорема 1.1. Нормальная кривизна любой линии поверхности, проходящей через точку M, с точностью до знака равна кривизне нормального сечения, имеющего с данной линии общую касательную (знак зависит от направления векторов и ).
3.9. Главные направления и кривизны поверхности
Исследуем
теперь вопрос, как меняется нормальная
кривизна в зависимости от направления
её вектора скорости. Как и для всякой
квадратичной формы, для второй квадратичной
формы найдётся ортонормированный базис
в касательной плоскости, в котором форма
имеет диагональный вид
![]() .
.
Определение
3.5.
Направления,
задаваемые векторами этого базиса,
называются
главными
направлениями,
а
числа
![]() – главными
кривизнами.
– главными
кривизнами.
Определение
3.6.
Произведение
![]() называется
гауссовой
или полной кривизной
поверхности
в данной точке,
полусумма
называется
гауссовой
или полной кривизной
поверхности
в данной точке,
полусумма
![]() – средней
кривизной.
– средней
кривизной.
Знание главных кривизн и главных направлений позволяет найти нормальную кривизну в произвольном направлении по формуле
![]() ,
,
где
![]() – угол между данным направлением и
направлением первого базисного вектора
(формула Эйлера).
– угол между данным направлением и
направлением первого базисного вектора
(формула Эйлера).
Из формулы Эйлера следует экстремальное свойство главных направлении: это те направления, где нормальная кривизна принимает наибольшее или наименьшее значение. Это свойство помогает находить главные направления: вектор с координатами du, dv задаёт главное направление, если выполнено условие:
![]() .
.
Главные кривизны
ищутся из условия
![]() ,
т.е. из уравнения
,
т.е. из уравнения
![]() .
.
