2.3. Соприкасающаяся плоскость кривой

П

Рисунок 3

усть PQ — касательная в точке Р к кривой γ (рис. 3). Через касательную PQ и точку M кривой проведем плоскость PQM. Плоскость π, к которой стремится плоскость PQM при М → Р, называется соприкасающейся плоскостью к кривой γ в точке Р.

Справедливо следующее утверждение.

Утверждение 2.1. Регулярная, дважды дифференцируемая кривая γ без особых точек имеет соприкасающуюся плоскость  каждой точке, в которой векторы и не коллинеарны.

Получим уравнение соприкасающейся плоскости в другой форме. Так как векторы – , , компланарны, то вектор удовлетворяет следующему уравнению

(2.1)

.

Если X, У, Z — координаты вектора (координаты переменной точки s плоскости π), а х(t), у(t), z(t) — координаты вектора , то в коор­динатной форме уравнение (2.1) запишется следующим образом:

(2.2)

.

Уравнение (2.2), очевидно, представляет собой уравнение соприка­сающейся плоскости.

Замечание 2.1. Соприкасающаяся плоскость определена гео­метрически с помощью предельного перехода, и поэтому в случае ее существования она будет единственна. Отсюда и из доказанного в этом пункте утверждения вытекает, что если в данной точке кривой существует соприкасающаяся плоскость, то при любой параметризации кривой вектор параллелен этой плоскости.

2.4. Длина дуги как параметр

Выберем на гладкой кривой : некоторую точку , соответствующую значению параметра и назовём её начальной точкой.

Длина дуги, имеющий начало в точке и конец в произвольной точке М, определяется, как известно из курса математического анализа, по формуле:

или в векторной форме .

Следовательно, длина дуги s  st является дифференцируемой функцией параметра t.

Так как производная этой функции во всех точках кривой, то функция s = s(t) является возрастающей функцией параметра t. Ввиду того, что все точки t кривой и значения длины дуги s находятся во взаимно однозначном и непрерывном соответствии, s можно принять за новый параметр. Такая параметризация называется естественной или натуральной параметризацией, где s – естественный или натуральный параметр. Так как , то и .

Отсюда следует, что – единичный вектор. Будем называть его единичным вектором касательной к линии в точке M и обозначать через , т.е. или . Тогда .

Задача 2.1. Найти длину дуги гиперболической винтовой линий заключённую между точками O и t. Параметризовать при помощи естественного параметра.

Решение. Найдём длину дуги . Вычислим отдельно

Тогда . Выразим из равенства параметр t. Имеем и, следовательно, .

Таким образом, получены естественные уравнения кривой

2.5. Кривизна кривой

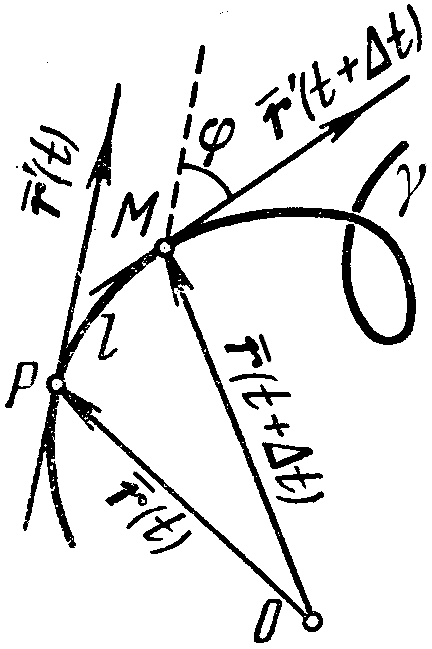Пусть Р — произвольная фиксированная точка регулярной кривой γ без особых точек и M — точка этой кривой, отличная от Р. Обозначим через φ угол между касательными в точках Р и М, а через s — длину дуги РМ (рис. 4).

О

Рисунок 4

пределение 2.7. Кривизной k кривой γ в точке Р называется предел отноше­ния φ / l при s→0 т. е. при М→P или .

Справедливо следующее утверждение.

Утверждение 2.2. Регулярная (дважды дифференцируемая) кривая γ без особых точек имеет в каждой точке определенную кривизну k.

Докажем это утверждение.

Пусть точки Р и М кривой отвечают соответственно значениям t и t+∆t параметра. Вычислим sin φ и s. Так как кривая γ регулярна, то ≠ 0 в любой точке кривой γ, и поэтому

(2.3)

,

(2.4)

,

где →0 при ∆t→0.

Отметим, что при преобразованиях выражения для s мы восполь­зовались формулой среднего значения для интеграла и непрерыв­ностью функции .

Преобразуем выражение (2.3) для sin φ. По формуле Тейлора

, α→0 при t→0.

С помощью этой формулы выражение (2.3) для sin φ принимает следующий вид:

(2.5)

где β→0 и ε→ 0 при ∆t→ 0.

Обращаясь к формулам (2.4) и (2.5) и используя при φ≠0 тождество

(при φ = 0 отношение равно нулю), получим

(2.6)

,

где β и μ стремятся к нулю при ∆t→ 0. Так как φ→ 0 при ∆t→0, то при ∆t→ 0. Поэтому из соотношения (2.6) следует, что при ∆t→0, т.е. M→P предел существует и равен . Утверждение доказано. ■

Итак, при условиях утверждения кривизна k существует и может быть найдена по формуле

(2.7)

.

З

(2.8)

амечание 2.2. Если в качестве параметра на кривой выбрана длина дуги s, так что , то 1 и вектор ортогонален вектору . В этом случае, очевидно, формула (2.7) примет следующий вид

.

На всей линии кривизна k есть функция параметра s, т.е. k=ks. Если в данной точке M имеем , то число называется радиусом кривизны линии в точке M.

Таким образом, если линия задана в естественной параметризации, то её кривизна вычисляется по формуле:

или в координатах:

.

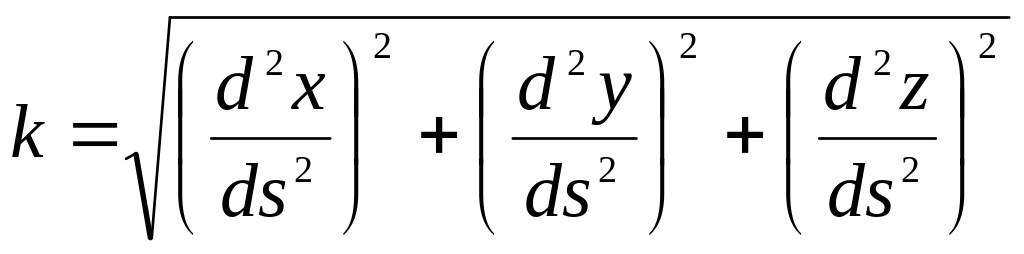Примем без доказательства следующее утверждение.

Утверждение 2.3. Для того, чтобы линия была простейшей (прямая, отрезок, луч) необходимо и достаточно, чтобы кривизна была равна нулю в каждой точке этой линии.