1.3. Интеграл от векторной функции по скалярному аргументу

Для вектор-функции , заданной на отрезке , как и для обычных скалярных функций, можно составить интегральные суммы и рассмотреть их предел при стремлении к нулю максимальной длины отрезков, на которые разбит отрезок [а, b]. Этот предел называется интегралом от по отрезку [а, b] и обозначается символом

При этом .

На интегралы от вектор-функций распространяются обычные свойства интегралов от скалярных функций.

2. Сведения из теории кривых

2.1. Элементарная кривая

Пусть M – любое множество точек пространства.

Определение 2.1. Если каждой точке поставлено в соответствие некоторая точка пространства, то говорят, что задано отображение f множества M в пространство.

Точка f (x) пространства называется образом точки x.

Множество точек f (M), составленное из образов всех точек множества M, называется образом множества M.

Отображение f множества M называется однозначным, если образы различных точек различны.

Пусть f – однозначное отображение. Тогда определено отображение , которое точке f (x) сопоставляет точку x. Это отображение называется обратным к f.

Определение 2.2. Отображение f множества M называется непрерывным, если какова бы ни была точка и число , существует число такое, что для любой точки расстояние , если расстояние .

Определение 2.3. Отображение называется гомеоморфизмом или топологическим отображением, если оно взаимно однозначно и взаимно непрерывно. Это значит, что f удовлетворяет двум условиям:

1. f – однозначное отображение;

2. f и 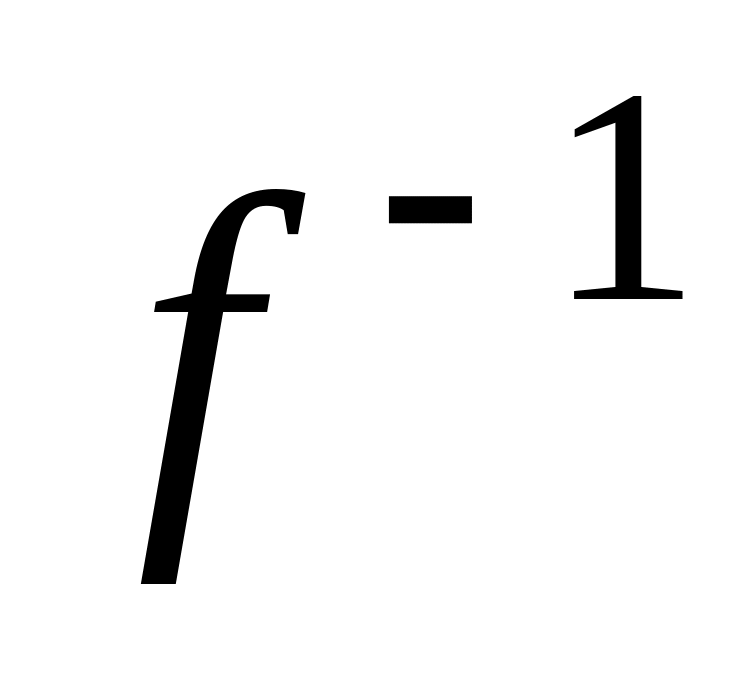– непрерывные отображения.

Относительно множества M и его образа говорят, что они гомеоморфны или топологически эквивалентны.

Определение 2.4. Множество точек пространства называется элементарной кривой, если это множество является образом открытого отрезка при топологическом отображении его в пространство (при гомеоморфизме).

Пусть – элементарная кривая и – отрезок, образом которого при отображении f является кривая; координаты точки кривой, соответствующие точке t отрезка.

Определение 2.5. Система равенств называется параметрическими уравнениями кривой .

Определение 2.6. Кривая называется регулярной (k – раз дифференцируемой), если функции имеют непрерывные производные до порядка k включительно. При k = 1 кривая называется гладкой.

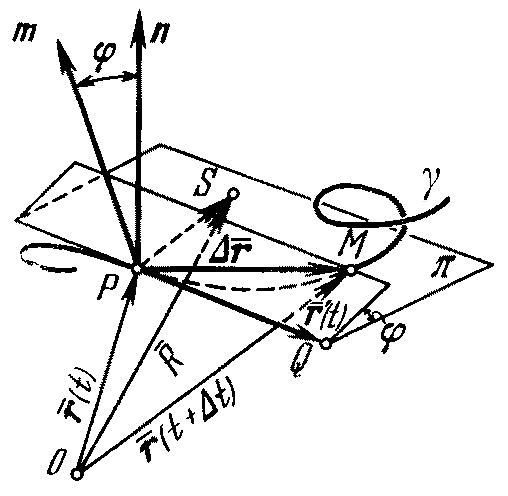
2.2. Касательная прямая к кривой

Пусть задана гладкая кривая , и её уравнение имеет вид или

.

Возьмём на линии две точки М и М₁, соответствующие значениям параметра t и (рис. 2). Вектор является направляющим вектором секущей прямой ММ₁. Следовательно, вектор также направляющий вектор секущей ММ₁. Когда , точка М₁ неограниченно приближается по кривой к точке М, вектор стремится занять положение касательной в точке М (касательная к кривой в точке определяется как предельное положение секущей).

Вместе с тем отношение стремится к производной как к своему пределу. Отсюда следует, что производная от радиус – вектора точки параметрической кривой есть вектор, направленный по касательной к этой кривой в сторону возрастания параметра t.

Чтобы получить уравнение касательной к вектор – функции, выразим радиус – вектор любой точки касательной прямой через радиус – вектор начальной точки, направляющий вектор и параметр .

Тогда – уравнение касательной в параметрическом виде.

Заменяя это векторное уравнение скалярными функциями, получим параметрические уравнения касательной:

или, исключив параметр , каноническое уравнение касательной:

.

Указанный способ определения касательной, очевидно, неприменим к той точке , для которой . Такие точки будем называть особыми точками кривой и будем исключать их из рассмотрения.