2.6. Кручение кривой

Пусть Р — произвольная фиксированная точка регулярной кривой без особых точек и М — точка этой кривой, отличная от Р. Обозначим через φ угол между соприкасаю­щимися плоскостями в точках Р и М, а через s – длину дуги РМ.

Определение 2.8. Абсолютным кручением |χ| кривой γ в точке Р назы­вается предел отношения φ/s при s → 0 (т. е. при М→Р).

Справедливо следующее утверждение.

Утверждение 2.4. Регулярная (трижды дифференцируемая) кривая γ без особых точек имеет в каждой точке, где кривизна отлична от нуля, определенное абсолютное кручение.

Докажем это утверждение.

П

(2.9)

усть точки Р и М кривой γ отвечают соответственно значе­ниям t и t + ∆t параметра. Нормали к соприкасающимся плоскостям в Р и М определяются векторами векторных произведений и . По формуле Тейлора с учетом равенства получим

где α → 0 при ∆t→ 0.

Для вычисления предела φ/s при s→0 нам понадобится значение синуса угла φ между нормалями к соприкасающимся плоскостям в точках Р и М. Для этой цели найдем модуль векторного произ­ведения и , а также произведение модулей этих векторов. С помощью (2.9) получим

Отсюда, используя распределительное свойство векторного произ­ведения и известную формулу для двойного векторного произведения, найдем

где , и поэтому β→0 при ∆t→0. Из последнего выражения для получаем следующую формулу:

(2.10)

где ε→0 при ∆t→0.

Путем аналогичных рассуждений получается также следующая формула:

(2.11)

где μ→0 при ∆t→0.

Из формул (2.10) и (2.11) получаем нужное нам выражение для sin φ:

.

Отметим, что в этом выражении значения производных векторной функции вычислены в точке Р.

(2.12)

.

Обращаясь к выражению (2.12) для s, используя только что полученную формулу для sin φ и известный предел при φ → 0, убедились, что предел при s → 0 существует и равен .

Итак, в условиях утверждения абсолютное кручение |χ| существует и может быть найдено по формуле

(12.22)

.

Определим кручение χ кривой с помощью равенства

(12.23)

(2.13)

.

2.7. Формулы Френе

Рассмотрим регулярную (трижды непрерывно дифференцируемую) кривую . Если в выбрана прямоугольная система координат, то .

Вектор является единичным вектором касательной к линии в точке M , где .

Вектор называется вектором кривизны линии в точке M и .

Прямая, проходящая через точку M в направлении называется главной нормалью линии в точке M (рис. 5).

Имеем , так как вектор – вектор постоянной длины и, следовательно, перпендикулярен вектору . Отсюда, главная нормаль перпендикулярна касательной.

Вектор называется единичным вектором главной нормали, т.е. =1. Так как , то и, следовательно, или

. (2.14)

Определим ещё вектор

Прямая, проходящая через точку M в направлении вектора называется бинормалью линии в точке M, а вектор – единичный вектор бинормали. Имеем, .

Плоскость, содержащая векторы и является соприкасающейся плоскостью; содержащая векторы и – нормальной плоскостью; содержащая векторы и – спрямляющей плоскостью.

Трёхгранник с вершиной в точке M, образованный этими тремя плоскостями, называются сопровождающим трёхгранником пространственной кривой (рис. 5).

Так как вектор – единичный, т.е. постоянной длины, то и значит вектор , параллелен спрямляющейся плоскости. Поэтому его можно разложить по векторам и

, (2.15)

где – координаты в базисе .

Тождество дифференцируем по параметру s: . Если в этом равенстве и заменить формулами (2.14) и (2.15), то получим или . Учитывая, что , т.к. это скалярное произведение единичных векторов, а , как скалярное произведение перпендикулярных векторов. Тогда будем иметь, что и, отсюда, . Формула (2.15) принимает вид после подстановки

. (2.16)

Тождество дифференцируем по параметру s:

.

Заменяя здесь векторы и их выражения через (2.12) и (2.14), находим, что

.

Отсюда или . Здесь взят знак “минус“, так как тройка векторов – левая; а число есть кручение линии в точке M.

М

(2.17)

ы получили следующие формулы Френе:

, , .

Вся теория гладких линии основана на применении этих формул.

Найдём формулу для вычисления кручения, если линия задана естественным уравнением или .

Первую формулу Френе можно записать так: . Продифференцируем это соотношение по s и используем вторую формулу Френе: , получим

.

Таким образом, смешанное произведение векторов по базису найдётся, как

.

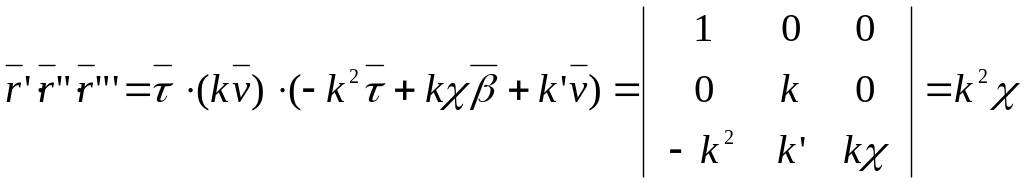Отсюда получаем искомую формулу для кручения линии:

(2.18)

или в координатах

(2.19)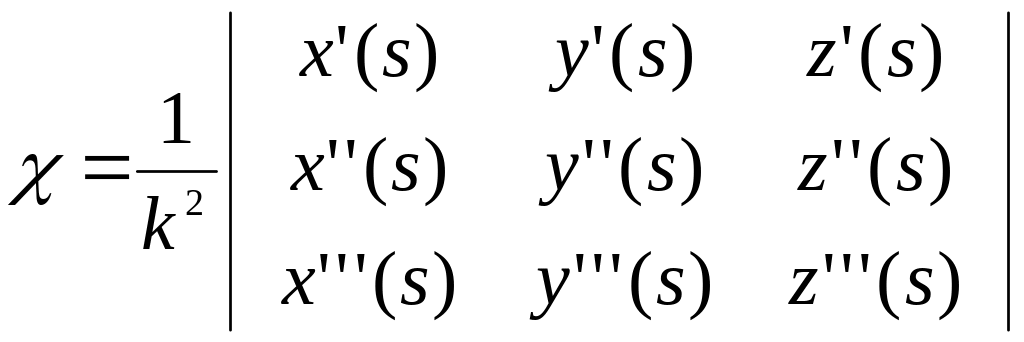

.

Линия называется плоской, если все её точки лежат в некоторой плоскости.

Примем без доказательства следующее утверждение.

Теорема 2.1. Кручение плоской линии во всех точках равно нулю.

Верно и обратное утверждение.

Пример 2.2. Найти кривизну и кручение винтовой линии , a>0.

Решение. Найдем производные вектор – функции

,

,

.

Теперь определим векторное произведение

Далее для смешанного произведения имеем

.

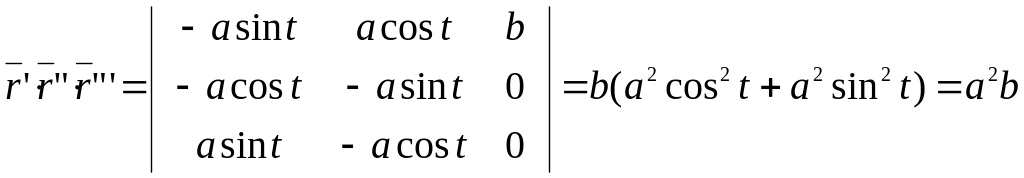Найдём длины векторов.

,

,

.

Отсюда кривизна будет равна , кручение .

Следовательно, для винтовой линии кривизна и кручение постоянны. ■