Однородная треугольная равнобедренная пластина массы с основанием и высотой .
Вычислим момент инерции пластины
относительно оси
,
проходящей через основание пластины
(Рис.5.6). В качестве элементарной площади
рассмотрим полосу параллельную оси
,
длина которой
,
а ширина –
.
Масса полосы равна
где
Из подобия треугольников получаем:
Учитывая, что все точки такой полосы расположены на одинаковом расстоянии от оси , получаем:
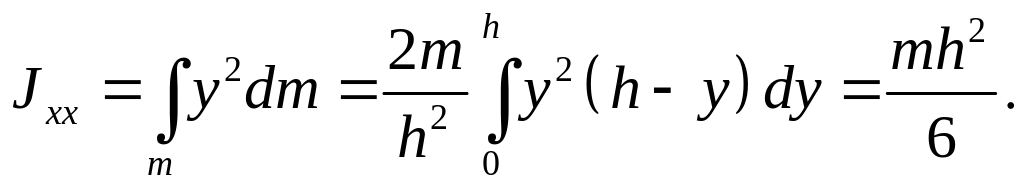
Используя теорему Гюйгенса–Штейнера, получаем:
При вычислении момента инерции пластины относительно оси используем формулу (5.5), поскольку элементарную полосу можно рассматривать как однородный стержень длины :
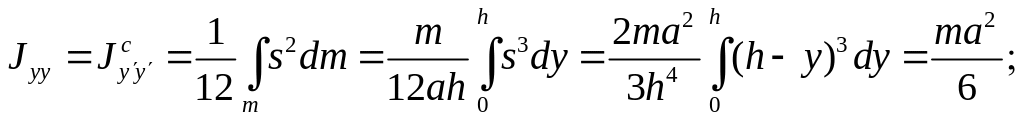
Вычисление кинетической энергии абсолютно твердого тела
Получим формулы для вычисления кинетической энергии абсолютно твердого тела при некоторых его движениях.
1. При поступательном движении в
любой момент времени скорости всех
точек тела одинаковые. Полагая в формуле
(4.18)
получаем:
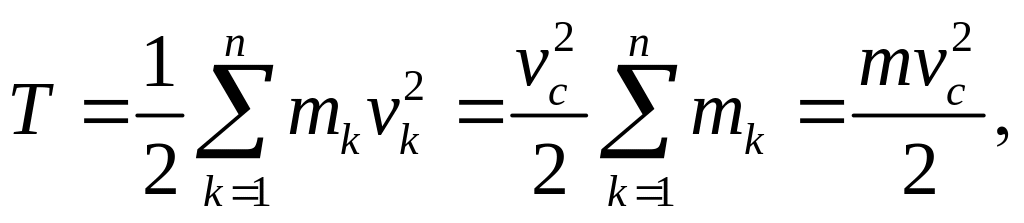(5.6)
где
– скорость центра масс тела.
2. При вращении скорости точек тела
пропорциональны расстояниям от точек
до оси вращения. Полагая в формуле (4.18)
получаем:
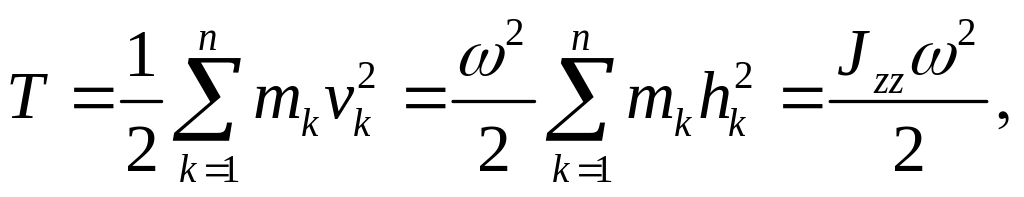(5.7)
где
– момент инерции тела относительно оси
вращения.
3. При плоско–параллельном движении тело по отношению к системе Кенига совершает вращение вокруг оси . Используя вторую теорему Кенига (4.32) и формулу (5.7), получаем:
(5.8)
где
– момент инерции тела относительно оси
Работа внутренних сил геометрически неизменяемой механической системы
Заметим, что в отличие от теоремы об изменении количества движения и теоремы об изменении кинетического момента в теорему об изменении кинетической энергии в общем случае входят внутренние силы.
Особый случай представляет геометрически неизменяемая механическая система, в частности, абсолютно твердое тело.
Скорости двух любых точек
и
геометрически неизменяемой механической
системы связаны известным кинематическим
соотношением:
причём
Эти две точки взаимодействуют с силами равными по модулю и направленными по одной прямой в противоположные стороны:
Заметим, что для механической системы эти силы являются внутренними.
Вычислим суммарную мощность этих двух сил:
т.к.
Поскольку внутренние силы действуют попарно, получаем, что суммарная мощность, а следовательно, и суммарная работа всех внутренних сил геометрически неизменяемой механической системы равна нулю при любых ее перемещениях.
Для геометрически неизменяемой механической системы теорема об изменении кинетической энергии является прямым следствием теоремы об изменении количества движения и теоремы об изменении кинетического момента. Тем не менее, ее использование часто оказывается удобным, особенно в тех случаях, когда необходимо определить зависимость каких–либо скоростей от перемещения, совершенного системой. Для геометрически изменяемой механической системы теорема об изменении кинетической энергии носит независимый характер.