Метод Паттерсона

Если построить ряд Фурье, коэффициентами которого являются структурные амплитуды, то можно найти распределение электронной плотности, максимумы которой соответствуют центрам атомов. Наряду с функцией электронной плотности можно ввести и другие функции, связанные с , которые вполне определенным образом зависят от координат атомов в кристалле.

В качестве такой функции можно брать так называемую функцию межатомных векторов (или межатомную функцию, или функцию Паттерсона).

Понятие межатомного вектора, вероятно, не нуждается в пояснении. Отметим, все же, что межатомный вектор абсолютно однозначно описывает положение двух атомов относительно друг друга. В этом смысле он несет вполне конкретную информацию о структуре объекта. Если задан межатомный вектор , то в структуре на расстоянии от одного из атомов, равном модулю , и в направлении, заданном этим вектором, расположен другой атом. Итак, если есть межатомный вектор с проекциями на координатные оси , то назовем межатомной функцией следующее выражение

(1)

Межатомная функция определяет среднее произведение электронной плотности на концах вектора .

Исходя из определения (1) можно найти выражение через , так как

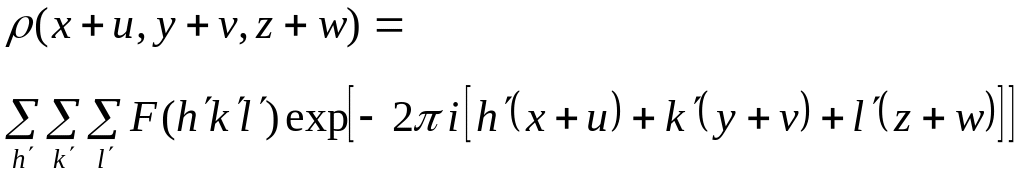. (2)

Индексы суммирования и не обязательно должны быть одинаковыми, ибо и определяются независимо.

Итак,

(3)

Рассмотрим один из интегралов

так как - целое число.

Но если , то интеграл

т.е. из бесчисленного множества сочетаний и ненулевой вклад в значение дадут только те пары индексов, которые связаны условием . Но

.

Отсюда, опуская штрихи , получим

. (4)

Следовательно, функция Паттерсона является трансформантой Фурье структурного фактора . Формула (4) не является окончательным выражением межатомной функции. Учтем, что для любой пары атомов А и В всегда . В соответствие с формулой Эйлера (с точностью до постоянного множителя) функция запишется

. (5)

Для того, чтобы подробнее говорить о применимости межатомной функции для описания структур кристаллов, рассмотрим связь между распределением атомов в кристалле и изображением этого распределения в векторном пространстве.

Межатомные векторы можно изобразить в специально выбранной системе координат точками, радиусы векторы которых равны этим межатомным векторам. Совокупность таких точек определит векторную систему кристалла.

Каждой точке векторного пространства мы можем приписать не только три координаты, но и ее «вес» численно равный по аналогии с функцией в пространстве кристалла.

Переход от пространства кристалла к векторному пространству

С практической точки зрения переход от пространства кристалла к векторному не представляет большого интереса, ибо если известна структура кристалла, то значит основная задача структурного анализа решена, и, кроме того распределение функции Паттерсона легко найти из эксперимента, т.к. в формуле для расчета фигурирует только . Считаем, что рентгенограмма проиндицирована. Мы осуществляем переход от пространства кристалла к векторному пространству для того, чтобы отыскать некоторые закономерности, облегчающие наиболее важный в практическом отношении переход от векторного к пространству кристалла.

П

редположим, что в пространстве кристалла существует набор атомов (пять атомов).

Рис.1

В прямом пространстве изображено пять точек. Нетрудно убедиться, что такая структура характеризуется набором из 20 межатомных ненулевых и пяти нулевых векторов. 20 точек не совпадают с началом координат, причем все они связаны центром симметрии, и еще пять точек располагаются в начале координат векторного пространства. Для построения векторной системы начало координат векторного пространства совмещают с точкой 1 пространства кристалла. Для этих целей удобно векторное пространство «изображать» на кальке.. Пр и таком совмещении получаются изображения векторов12, 13, 14, 15 . Затем калька параллельно переносится в положение, когда начало координат ее системы совпадает с точкой 2 и строятся векторы 23, 24, 25, 21 и т.д.В точке О кроме того расположены пять векторов 11, 22, 33, 44, 55. В конечном итоге получается векторная система, изображенная на р

ис.

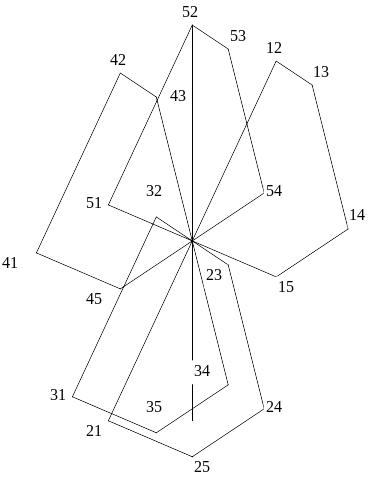
Рис.2

Следовательно, если в кристалле атомы расположены так, как это показано на рис.1, то при подстановке в ряд Фурье (2) структурного фактора будет получено распределение, изображенное на рис 2.

Это распределение пока еще не позволяет говорить о структуре объекта, т.к. это распределение межатомных векторов, а не атомов. Рис.2 иллюстрирует связь между векторным пространством и пространством кристалла. Видно, что в векторном пространстве можно выделить пять трансляционно идентичных и еще пять центрально симметричных структур, соответствующих структуре изучаемого кристалла.

Конечно, при возрастании числа атомов в кристалле картина распределения векторов значительно усложняется, и переход от векторного пространства к пространству кристалла может быть очень затруднителен.

В трехмерном варианте переход от кристаллического пространства к векторному пространству осуществляется аналогичным образом. При этом, как и в плоском случае, если в кристалле есть атомов, то в векторном пространстве будет ненулевых и нулевых векторов. Кроме того, в векторном пространстве можно выделить фигур, равных аналогичной в пространстве кристалла, и связанных с первой группой центром симметрии.

На практике часто приходится иметь дело со структурами, в которых есть несколько одинаковых межатомных векторов. В этом случае точки, изображающие их в векторном пространстве, будут налагаться, что очень затрудняет интерпретацию полученного распределения. Например, при построении в векторн6ом пространстве изображения квадрата, у которого вершины последовательно обозначены 1, 2, 3, 4. Получим совпадение векторов 12 и 34. Совпадут также 23 и41 (естественно, совпадут и их обратные вектора). В векторном пространстве будет всего 8 ненулевых векторов.

Кроме того, мы рассмотрели преобразования для точечных фигур, но

,

а практически во всех точках кристалла. Следовательно, на распределении

Нужно проводить изоповерхности (трехмерный случай) или изолинии (двумерный случай), т.е. применять ту же методику, что и при построении распределений электронной плотности. Максимумы функции Паттерсона определяют положения точек в векторном пространстве соответствующих межатомным векторам в пространстве кристалла.

Векторное пространство обладает некоторыми специфическими особенностями, которые значительно понижают точность определения координат атомов.

1 Рентген Вильгельм Конрад (27.03.1845–10.02.1923) немецкий физик-экспериментатор, чл.-корр. Берлинской АН (1896). Родился в Леннене. Окончил Цюрихский политехникум. В 1871–1873 гг. работал в Вюрцбургском, в 1874–1879 гг. в Страсбургском университетах, в 1879–1888 гг. профессор университета в Гиссене и директор Физического института, с 1888–1900 гг. – профессор Вюрцбургского университета (в 1894 г. избран ректором) в 1900–1920 гг. – профессор Мюнхенского университета и директор Физического института. Научные исследования относятся к электромагнетизму, физике кристаллов, оптике, молекулярной физике. В 1895 г. открыл излучение, названное впоследствии его именем, исследовал его природу и свойства (первая Нобелевская премия по физике, 1901 г.). В 1885 г. открыл магнитное поле диэлектрика, движущегося в электрическом поле (рентгенов ток), что имело важное значение для создания электронной теории. Открыл взаимосвязь электрических и оптических явлений в кристаллах. Учениками Рентгена были М. Вин, А. Ф. Иоффе, П. Книппинг, Р. Ладенбург, В. Фридрих и др.

2 Баркла Чарльз Гловер (27.07.1877–23.10.1944) – английский физик, член Лондонского королевского общества. Родился в Уиднессе. Окончил Ливерпульский университет 1899. В 1905–1909 гг. работал в Ливерпульском, в 1909–1913 гг. – в Лондонском университетах. С 1913 г. – профессор Эдинбургского университета. ^. Основные работы посвящены физике рентгеновских лучей. В 1904 г. осуществил поляризацию рентгеновских лучей, доказав тем самым их волновую природу. В 1906 г. открыл характеристические рентгеновские лучи (Нобелевская премия по физике, 1917 г.).

3 Мозли Генри (23.09.1987–10.08.1915) английский физик один из основоположников рентгеновской спектроскопии. Родился в Уэймуте. Окончил Оксфордский университет (1910). В 1910–1914 гг. работал в Манчестерском университете под руководством Э. Резерфорда. Во время Первой мировой войны ушел добровольцем на фронт и погиб. Работы в области бета-, гамма- и рентгеновской спектроскопии. Измерил длины волн рентгеновского излучения, предсказал рентгеновские спектры ряда элементов, обнаружил связь частоты спектральных линий характеристического рентгеновского излучения с порядковым номером излучающего элемента (закон Мозли).