2. Вектор валового выпуска, вектор конечного потребления, матрица прямых затрат.

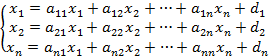
А = - матрица прямых затрат (матрица Леонтьева)

3. Уравнение межотраслевого баланса. Модель Леонтьева. Продуктивная матрица.

– уравнение межотраслевого баланса (уравнение Леонтьева). Межотраслевой баланс — экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны. Основная задача межотраслевого баланса состоит в нахождении такого вектора валового выпуска , который при известной матрице прямых затрат A обеспечивает заданный вектор конечного продукта . Зная матрицу А и вектор остаётся решить уравнение

. Матрица А=>0 называется продуктивной, если для любого вектора существует решение уравнения Леонтьева.

4. Первый и второй критерии продуктивности.

1-ый кр. прод: Матрица А=>0 продуктивна тогда и только тогда, когда матрица

существует и неотрицательна.

2-ой кр. прод: Неотрицательная квадратная матрица А продуктивна тогда и только тогда, когда её число Фробениуса меньше единицы.

5. Докажите, что матрица A ≥ 0 продуктивна тогда и только тогда, когда матрица − существует и неотрицательна (первый критерий продуктивности).

Пусть существует =>0, тогда x=(E-A)^-1y, где оба множителя >0, следовательно, x=>0, значит матрица продуктивна. Пусть А продуктивна. (E-A)x=e₁, значит с₁=>0, (E-A)x=e₂, значит с₂=>0, следовательно, (с₁,с₂,c_n)=C=>0. (E-A)C=E=>C=(E-A)^-1=>0

6. Докажите, что если неотрицательная квадратная матрица продуктивна, то ее число Фробениуса меньше 1.

Матрица А≥0 называется продуктивной, если для любого вектора ≥0 существует решение ≥0 уравнения

Пусть матрица А – неотрицательна и продуктивна.

Тогда для любого неотрицательного вектора существует решение ≥0 уравнения

Пусть >0, тогда, очевидно, >0. Умножив слева еа левый вектор Фробениуса и учитывая, что

A= , то получим

>0, >0, то >0, >0. Поэтому из последнего равенства вытекает, что <1.

7. Задача оптимизации. Допустимое множество. Целевая функция.

Задача оптимизации - общая задача математического линейного программирования: найти экстремум целевой функции и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений.

Математическая модель: f(ẍ)--->max(min) при условии ẍϵХ

Целевой функцией f(ẍ) называют функцию от переменных задачи, которая характеризует качество выполнения задачи.

Множество Х называется допустимым, а любая его точка ẍϵХ – допустимым решением (планом).

8. Оптимальное решение. Оптимальное множество. Задача линейного программирования (злп).

Множество Х называется допустимым, а любая его точка ∈ X −допустимым решением (планом). Точка *∈ X , для которой f ( *) – наибольшее (наименьшее) значение f ( ) на Х, называется оптимальным решением (планом).

Оптимальное множество – множество оптимальных решений.

Если целевая функция¹ и система ограничений² линейны, то задача математического программирования называется задачей линейного программирования (сокращенно, ЗЛП).

9. Примеры злп. Задача о банке, задача о диете, задача об использовании ресурсов.

1) Задача о банке. Пусть собственные средства банка в сумме с депозитами составляют S млн долл. Часть этих средств, но не менее K млн долл., должна быть размещена в кредитах. Кредиты являются неликвидными активами банка, так как в случае непредвиденной потребности в наличности обратить кредиты в деньги без существенных потерь невозможно.

Другое дело ценные бумаги (особенно государственные). Их можно в любой момент продать, получив некоторую прибыль или, во всяком случае, без большого убытка. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определенной пропорции ликвидные активы – ценные бумаги, чтобы компенсировать неликвидность кредитов. В нашем примере ликвидное ограничение таково: ценные бумаги должны составлять не менее p% средств, размещенных в кредитах и ценных бумагах.

Пусть x – средства (млн долл.), размещенные в кредитах, y – средства, вложенные в ценные бумаги. Имеем следующую систему линейных ограничений:

1) x+y ≤S – балансовое ограничение;

2) x+K – кредитное ограничение;

3) y ≥0,01p(x+y) – ликвидное ограничение;

4) x ≥0, y ≥0.

Цель банка состоит в том, чтобы получить максимальную прибыль от кредитов и ценных бумаг: → max при условиях 1) – 4), где – доходность кредитов, – доходность ценных бумаг.

Так как кредиты менее ликвидны, чем ценные бумаги, то обычно . Мы пришли к задаче линейного программирования с ограничениями 1) – 4) и целевой функцией f, которую требуется максимизировать.

2) Задача о диете. Известно, что 1 кг яблок стоит 30 руб., а 1 кг абрикосов 60 руб. Сколько яблок и абрикосов должен потреблять человек в сутки, чтобы получить не менее 70 мг витамина С и не менее 2 мг витамина А при минимальных затратах на яблоки и абрикосы? Содержание витаминов А и С в яблоках и абрикосах указано в таблице.

	А (мг/кг)	С (мг/кг)
Яблоки	1	70
Абрикосы	24	75

при

Где - суточое потребление яблок и абрикосов в кг

Общая форма

Задача о диете: Пусть имеется 2 вида продуктов П₁ и П_2, содержащих питательные вещества А,В,С. В 1кг продуктов П₁ и П₂ содержится определенное количество вещества того или иного вида.

	А	В	С
П1	а1	b1	C1	Х1
П2	а2	b2	C2	Х2
	А	B	C

a,b,c- ежесуточное потребление А, В и С соответственно

s_1,s₂- стоимость П₁ и П₂ соответственно

Тогда целевая функция f=s₁x₁+s₂x₂-->min

Система ограничений:

Задача об использовании ресурсов: пусть R₁, R₂,R₃ – наличные ресурсы

b₁,b₂,b₃ – количество ресурсов R₁,R₂,R₃ соответственно

Т₁,Т₂ – выпускаемые товары

a_ij- число единиц ресурса, необходимых для выпуска 1 единицы товара

с₁,с₂ – доход от продажи товаров Т₁, Т₂ соответственно

х₁, х₂ – количество товаров Т₁ и Т₂ соответственно

общее количество ресурса R_1, используемого при выпуске обоих товаров, равное , не должно превосходить b_i , т.е. должны выполняться неравенства , i=1,2,3

Тогда целевая функция f=c₁x₁+c₂x₂--->max система ограничений:

Другие задачи ЗЛП:

- задача об оптимальном портфеле ценных бумаг

- задача о заготовках

- транспортная задача