48. Наибольшее и наименьшее значения непрерывной функции на замкнутом ограниченном множестве.

Множество S называется ограниченным, если оно содержится внутри круга (для множества на плоскости) или внутри шара (для множества в пространстве), имеющего достаточно большой радиус. Множество называется замкнутым, если оно включает в себя все свои предельные точки.

Важным свойством непрерывных функций является следующее.

Пусть z= f(x,у) — непрерывная функция, a S — замкнутое и огра­ниченное множество, лежащее в области определения функции f. Тогда в S существуют точки, в которых функция принимает свои наиболь­шее и наименьшее значения, множество значений представляет собою отрезок [f_наим,f_наиб].

49. Кратные интегралы и их свойства. Условия интегрируемости функции.

Определение. Если существует конечный предел интегральных сумм при ʎ->0 то функция f(x;y) называется интегрируемой в области D. Значение этого предела называется двойным интегра­лом по области D

свойства двойного интеграла.

1. Если функция f(x;y) интегрируема в области D, то для любого числа к функция kf(x;y) также интегрируема в D и

2. Если функции f(x;y) и g(x;y) интегрируемы в области D, то их алгебраическая сумма также интегрируема в этой области и

3. Если функции f(x;y) и g(x;y) интегрируемы в области D и f(x; у) <= g(x; у) во всех точках D, то

4. Если функция f(x;y) ограничена на множестве Г нулевой площади, то

5. Свойство аддитивности интеграла. Если область интегрирова­ния D может быть разбита на две части D₁ и D₂, не имеющих общих внутренних точек, так, что D=D₁ объединение D₂, и f(x;y) интегрируема в D₁ и D₂, то в области D эта функция также интегрируема, и

6. Теорема о среднем. Если функция f(x;y) непрерывна в области D, то в этой области найдется такая точка (о, т ), что

Если функция f(x, у) определена и непрерывна в прямоугольнике Р = {a=<х=<b, с=<у=<d), то существует двойной интеграл P

Пусть G — ограниченная область, f— ограничен­ная функция на G,Г — объединение границы G и множества точек разрыва f на G. Предположим, что площадь Г равна нулю. Тогда

существует интеграл G

50. Сведение кратного интеграла к повторному интегралу.

Если функция f(x,y) интегрируема в области G и при любом фиксированном х из [а,b] существует интеграл справедлива формула

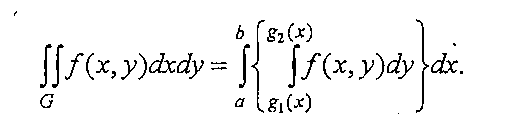
51. Формула замены переменных в двойном интеграле. Использование полярных координат для вычисления двойных интегралов.

В полярных координатах :

52. Геометрические приложения двойных интегралов: вычисление площадей плоских фигур и объемов пространственных тел.

Определение. Если существует конечный предел интегральных сумм при ʎ->0 то функция f(x;y) называется интегрируемой в области D. Значение этого предела называется двойным интегра­лом по области D

Геометрический смысл двойного интеграла.

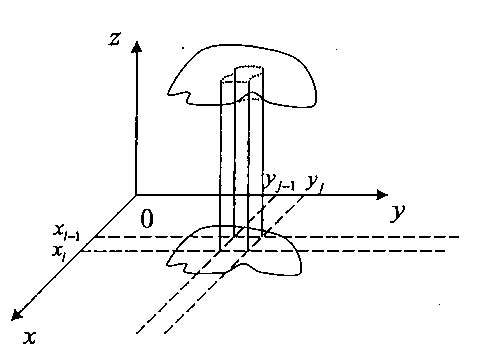
Рассмот­рим непрерывную неотрицатель­ную функцию z = f(x;y)>=0 при любом значении (x,y) принадлежащем D. Ее графиком будет поверхность в пространстве OXYZ. Тогда двойной интеграл D представляет собой объем прямого цилиндрического тела, ограниченного снизу областью D, а сверху поверхностью z= f(x;y).

Если подынтегральная функция f(x;y) тождественного равна единице в области D, то значение двойного интеграла совпадает с площадью области интегрирования: