§2. Особенности математических вычислений на эвм. Погрешности вычислений

Для правильного решения прикладных задач на ЭВМ очень важно признать, что получить точное значение интересующей величины практически не возможно и не в этом цель вычислений. Получаемое на ЭВМ решение y почти всегда (за редким исключением) содержит погрешность, т.е. является приближенным.

Пусть y  точное значение величины, вычисление которой является целью поставленной задачи, y^* - получаемое на ЭВМ решение. Различие между величинами y и y^* определяет величину погрешности y.

Погрешность _нy - соответствующая первым двум причинам называется неустранимой погрешностью. Такое название вызвано тем, что математическая модель и исходные данные вносят в решение ошибку, которую нельзя устранить в процессе дальнейшего решения. Погрешность _мy источником которой является метод решения, называется погрешностью метода, а погрешностью _вy - возникающую при вводе, вычислениях и выводе называют вычислительной погрешностью.

Полная погрешность результата решения задачи на ЭВМ y=y-y^* складывается из этих трех погрешностей: y=_нy+_мy+_вy; желательно, чтобы и .

ЭВМ обрабатывает числа, которые записаны в форматах с фиксированной запятой и плавающей запятой.

Рассмотрим десятичные действительные числа с фиксированной запятой: 5.1; -10.2; 175.12; 0.0093 и т.п. Эти же числа можно представить в виде: ;- ; , т.е., в общем случае, , где к - разрядность мантиссы числа, n - порядком числа.

Из этой записи следует, что действительные числа, с которыми оперирует ЭВМ не являются бесконечными, т.к. разрядность к и границы порядка n конечны. Обычно к=7, а .

Таким образом, число будет представлено в ЭВМ в виде , т.е. приближенно и отличаться от истинного значения на величину .

Процесс представления числа с меньшим количеством разрядов называется округлением. Существует несколько способов округления. Наиболее простой из них – усечение (отбрасывание), состоит в отбрасывании меньших разрядов. Чаще используется округление по дополнению (симметрическое), в котором, если первая слева отбрасываемая меньше 5, то сохраняется значение младшего сохраняемого разряда, если же отбрасываемая цифра , то к младшему сохраняемому разряду добавляют единицу.

Следовательно, ЭВМ оперирует с приближенными значениями действительных чисел. Мерой точности приближенных чисел является погрешность.

Максимальная относительная погрешность ЭВМ, связанная с округлениями при вводе, выводе и выполнении арифметических операций называется машинным эпсилон и обозначается _,, она характеризует точность ЭВМ.

Простейшей количественной мерой ошибки является абсолютная погрешность:

, (2.1)

где >0 -положительная величина. Это равенство можно разделить на два:

.

Рассмотрим равенство со знаком “+”: . Возьмем модуль: (по правилу треугольников). Отсюда

, . (2.2)

Рассмотрим равенство со знаком « – » : . Возьмем модуль: . Имеем: или

, . (2.3)

По величине абсолютной погрешности не всегда можно сделать правильное заключение о качестве приближения. Пусть . Много это или мало? Ответ зависит от величины а. Если а=0,2, то погрешность велика, если а=10⁶, то погрешность мала. Естественно соотнести погрешность величины и ее значение. Для этого вводится относительная погрешность величины а.

. (2.4)

Максимальное значение абсолютной погрешности называется предельной абсолютной погрешностью и обозначается .

Максимальное значение относительной погрешности называется предельной относительной погрешностью и обозначается

На основании этих определений можно записать:

Погрешность приближенного числа связана с количеством его верных знаков.

На практике количество верных знаков числа обычно отсчитывается от первой значащей цифры числа до первой значащей цифры его абсолютной погрешности: например, число S=20,7426 с абсолютной погрешностью имеет три верных знака (2,0,7); остальные знаки - сомнительные. Также считают, что количество верных знаков числа равно порядку относительной погрешности, взятому с противоположным знаком, т.е. наличие одного верного знака соответствует относительной погрешности порядка 10%, двух верных знаков - погрешности порядка 1%, трех верных знаков - погрешности порядка 0,1% и т.д.

В математических таблицах все числа округлены до верных, при этом абсолютная погрешность чисел не превосходит половины единицы последнего оставленного разряда. Например, если в таблице указано е=2,718, то абсолютная погрешность не превосходит .

В окончательных результатах вычислений обычно оставляют, кроме верных знаков, один сомнительный знак.

Правила оценки погрешностей.

а) При сложении и вычитании чисел их абсолютные предельные погрешности складываются; (2.5)

б) При умножении и делении чисел друг на друга их относительные предельные погрешности складываются;

(2.6) т.к. и , то: , следовательно:

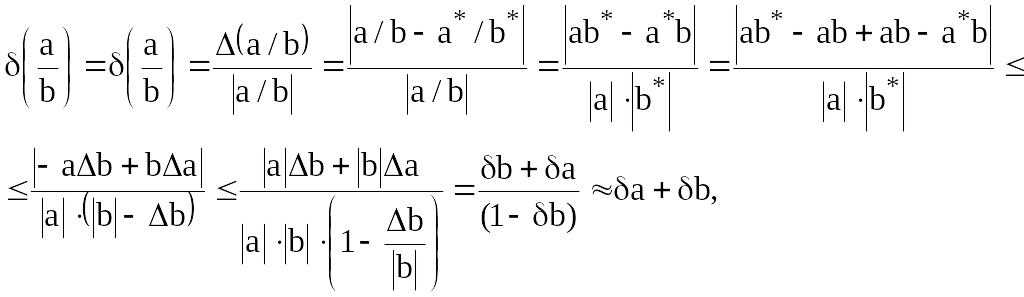(2.7)

т.к. .

в) При возведении в степень приближенного числа его относительная предельная погрешность умножается на показатель степени.

В дальнейшем под погрешностью мы будем понимать предельную погрешность (эту величину можно измерить, рассчитать, оценить), поэтому значок - вверху у предельных погрешностей ставить не будем.

г) погрешности функций. Рассмотрим функцию одной переменной y=f(x). Пусть а - значение аргумента x, - абсолютная погрешность, т.е. .

Абсолютную погрешность функции можно считать ее приращением, которое можно заменить дифференциалом: . Тогда для оценки абсолютной погрешности имеем

(2.8)

Относительная погрешность функции определяется как:

(2.9)

Аналогичные выражения можно записать для функции нескольких переменных: xa, yb, zc;

(2.10)

В привычной нам позиционной десятичной системе счисления вещественное число “x”: представляется последовательностью символов (цифр от 0 до 9), которая начинается со знака (“+” или “-“) и продолжается цепочкой десятичных цифр a_i и b_i разделенных десятичной точкой:

x = a_na_n-1...a₁a₀ . b₁b₂...b_m. (2.11)

В выражении (2.11) каждой позиции (месту), которую занимает цифра относительно десятичной точки, отвечает определенная степень числа 10, которую называют основанием. По существу, равенство (2.11) представляет собой сокращение записи числа “x”, имеющей вид:

Пример 1. Запись x=20.5 означает:

a₀=0, a₁=2, b₁=5.

Для представления чисел в вычислительных машинах также используют позиционные системы счисления, однако основаниями системы служат, как правило, степени числа 2. Это вызвано способом хранения чисел в устройствах памяти ЭВМ, т.к. триггеры - основа оперативной памяти имеют два состояния 0 или 1. В двойной системе чисел 2=10, число 4=100, и т.д.

На базе двойной системы счисления можно создать системы счисления с основаниями где n=1,2,3,..., т.е. cистемы счисления с основаниями 2,4,8,... и т.д. Наиболее распространены системы счисления 2,8 и 16.

В базовой двоичной системе число x представляется в виде:

Пример 2. Запишем число 20,5 в двоичной системе . Следовательно: или сокращенно: (10100.1)₂.

где L - некоторое стандартное для ЭВМ целое число, - двоичные цифры (0,1). Всего для хранения числа n отводят L+2 разрядов ( один из них для хранения знака ).

В большинстве современных ЭВМ для вещественного числа принята форма представления с плавающей запятой, когда каждое число представляется в виде: (2.12)

Здесь двоичные цифры. Число x нормализуется так, что всегда , и поэтому в памяти ЭВМ хранятся только значащие цифры. Число называется мантиссой числа x. Количество t цифр, которое отводится для записи мантиссы, называется разрядностью мантиссы, зависит от типа ЭВМ, но всегда является конечным. В представлении (4) p - целое число, называется двоичным порядком.

Порядок также записывается как двоичное целое число для хранения которого в машинном слове отводится L+2 двоичных разрядов. Поскольку нуль - не нормализуемое число (его нельзя представить в виде (2.12) у которого ), для его хранения предусматривают особую запись.

Пример: x=20.5 в двоичной системе имеет вид x=(10100.1)₂. Переместим точку на 5 позиций влево, получаем

Пример. Рассмотрим гипотетическую ЭВМ, в которой числа представляется лишь 6 двоичными разрядами мантиссы, а округление производится по дополнению. Вычислим сумму и произведение двух чисел а=20.5= и

.

Проведем вычисление в двоичной арифметике:

,

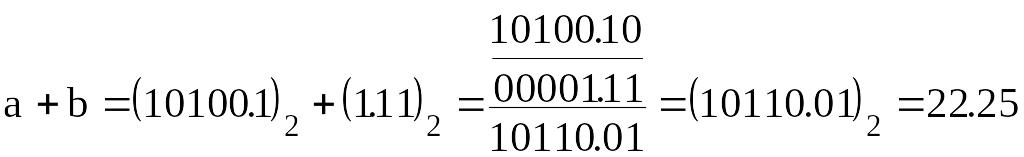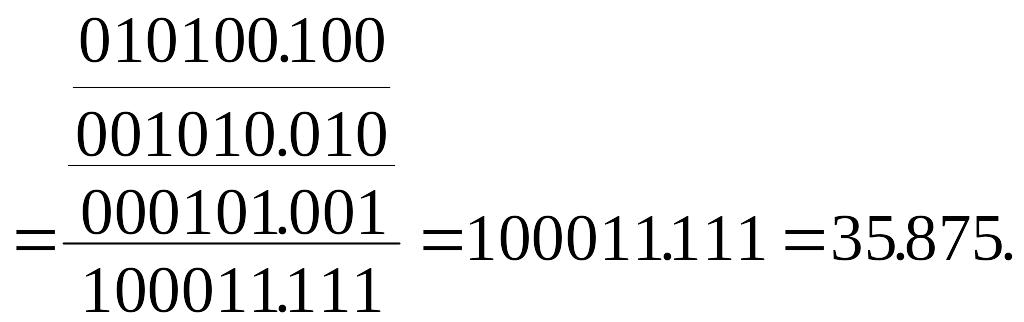
После округления до 6 значащих цифр получим:

Таким образом из-за округления мы получим значения отличающиеся от истинных, при этом величины абсолютной погрешности соответственно равны:

Заметим, что машинные арифметические операции обладают несколько иными свойствами чем арифметические операции. Например, не выполняется известное правило коммутативности: a+b=b+а.

Пусть Тогда Далее После округления: Сложение в ином порядке дает далее Таким образом

Округления с помощью табличного процессора Excel

В табличном процессоре Excel существует ряд функций, предназначенных для округления значений. Например, функция ОКРУГЛ, округляет значение до необходимого разряда симметрическим методом, при этом указывается округляемое число и количество разрядов, после запятой в результате округления, причем округлять можно, не только какое-то конкретное значение, но и результат арифметических действий или значений функций. Так на рис.2.1 приведено округление результата выражения 2,547 : 5,068969 .

Рисунок 2.1. Выполнение округления в Excel

Имеются также следующие функции округлений:

ОКРУГЛВВЕРХ - Округляет число до ближайшего большего по модулю.

ОКРУГЛВНИЗ - Округляет число до ближайшего меньшего по модулю значения.

ОКРВВЕРХ - Округляет с избытком до ближайшего числа, кратного точности.

ОКРВНИЗ - Округляет число до кратного заданной точности с недостатком.