VІ. Змістовий модуль 5

Коливання та хвилі

Теоретичне ядро

Кінематика гармонічного коливального руху точки

Коливальний рух. Класифікація коливань. Гармонічні коливання.

Одним з найпоширеніших типів механічних рухів є коливальний рух або механічні коливання. Коливаннями називаються процеси, які відрізняються тією чи іншою ступінню повторюваності, тобто процеси, яким властива та чи інша ступінь повторюваності або періодичності механічного стану руху точки (тіла).

Приклади: від коливального руху атомів і молекул і до коливальних процесів, що відбуваються в мегасвіті. Вони відіграють як позитивну, так і негативну роль. Коливальні рухи можна поділити на 2 класи: періодичні і аперіодичні. Коливання, при яких механічний стан руху тіла точно повторюється через рівні проміжки часу, називаються періодичними. В противному випадку – аперіодичними.

Рис. 5.1

Періодичний рух математично описується функцією:

,

де Т– період коливань.

Більшість коливань в природі – аперіодичні. Періодичні коливання поділяються на гармонічні і негармонічні. Найпростішим типом коливальних рухів є гармонічні коливання. Гармонічними називаються коливання, при яких відстань коливальної точки до положення рівноваги (зміщення) змінюється з часом за законом синуса чи косинуса (тобто згідно гармонічного закону)

(5-1)

Одержане рівняння носить назву кінематичного рівняння гармонічних коливань. За характером траєкторії гармонічні коливання можуть бути прямолінійними (пружний маятник) і криволінійними (математичний маятник). Для криволінійних гармонічних коливань рівняння руху має вигляд:

,

де s – дугова координата.

Графік гармонічних коливань (дослід з пісочним маятником):

Рис.5.2

Ангармонічні коливання графічно зображуються наступним чином:

Рис.5.3	Рис.5.4

Кінематичні характеристики гармонічних коливань.

Період – інтервал часу між двома суміжними однаковими механічними станами руху коливальної точки.

Амплітуда – модуль найбільшого зміщення точки від положення рівноваги:

.

Зміщення – відстань точки, яка знаходиться в коливальному русі, від положення рівноваги і виражається прямолінійною або дуговою координатою даної точки: х або s. Визначає положення точки на траєкторії руху.

Фаза – величина, що залежить від часу і визначає як положення, так і напрям коливання в будь-який момент часу. Визначається аргументом sin або cos

,

де φ₀ – початкова фаза.

Циклічна (кругова) частота – величина, що визначає число коливань за 2π секунд. Це витікає із формули:

,

де 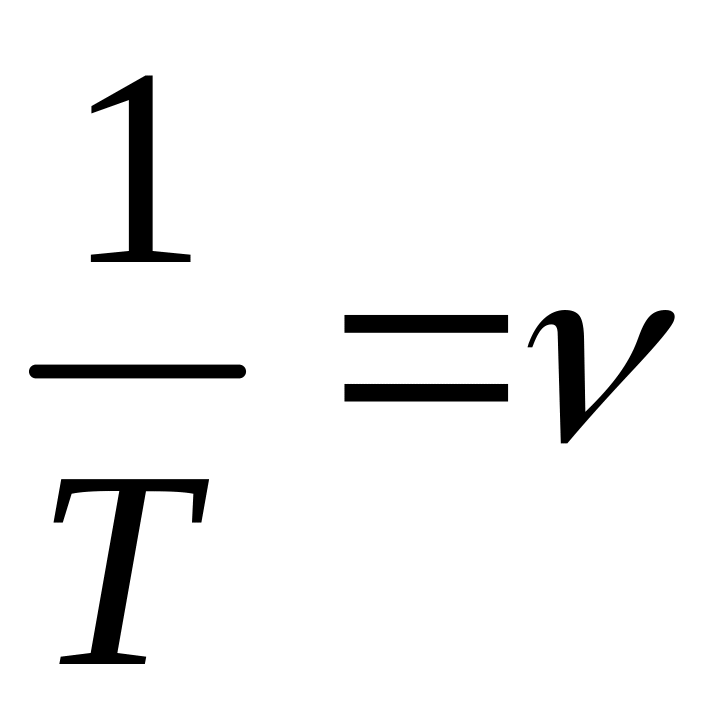– лінійна частота, визначає число коливань за одиницю часу. Тоді: .

Фази коливань, що відрізняються на 2π називаються однаковими, так як їм відповідає одне і те ж положення та напрям руху коливної точки. Фази коливань, що відрізняються на π називаються протилежними.

Швидкість і прискорення точки при гармонічному коливанні.

Використаємо рівняння гармонічних коливань:

(5-2)

Тоді: (5-3) , де – амплітуда швидкості.

Порівнюючи (5.2) і (5.3), робимо висновок, що швидкість приймає максимальне значення тоді, коли точка проходить положення рівноваги і дорівнює 0, тобто коли точка досягає максимального відхилення від положення рівноваги.

Вираз (5.3) перепишемо наступним чином:

(5-4)

Порівнюючи (5.4) з (5.2), маємо, що швидкість випереджає за фазою зміщення на , тобто за часом: , .

Диференціюючи за часом вираз для швидкості, маємо:

; .

, де – амплітуда прискорення.

Порівнюючи останній вираз з (5.2), маємо, що прискорення і зміщення одночасно перетворюються в 0 і одночасно досягають максимального значення.

Якщо останні вираз переписати наступним чином: , то можна зробити висновок, що прискорення випереджає за фазою зміщення на π раз або на півперіод за часом , тобто прискорення і зміщення змінюються в протифазі (протилежних фазах).

Так як , а , то .

Прискорення при гармонічних коливаннях пропорційне зміщенню і направлене до однієї і тієї ж точки – до положення рівноваги.

Рис. 5.6.

якщо х > 0, то а < 0;

якщо х < 0, то а > 0.

Зв’язок гармонічного коливання з обертальним рухом. Графічний метод опису гармонічного коливання.

Розглянемо рівномірний обертальний рух математичної точки, описавши його векторним способом. Нехай радіус-вектор , що визначає положення цієї точки відносно плоскої системи відліку ОХУ, рівномірно обертається навколо центра О з кутовою швидкістю ω. Розглянемо проекцію радіус-вектора на вісь ОХ.

, де (φ₀ –кут між вектором і віссю ОХ в момент часу t=0) а . Тоді одержимо: , тобто маємо рівняння гармонічного коливання матеріальної точки.

Таким чином, проекцію кінця радіус-вектора, що обертається з кутовою швидкістю ω можна розглядати як зміщення точки при гармонічному коливанні, причому циклічна частота коливань дорівнює кутовій швидкості обертання радіус-вектора, а амплітуда коливань – його модулю.

Рис. 5.7.

Звідси випливає графічний метод опису гармонічних коливань, який називають методом векторних діаграм. Він ґрунтується на тому, що гармонічне коливання можна задати за допомогою радіус-вектора математичної точки, що обертається з кутовою швидкістю рівною циклічній частоті коливань, а модуль радіус-вектора дорівнює амплітуді коливань.