
- •Дифференциальное исчисление функции одной переменной
- •Исследование функции методами дифференциального исчисления и построение её графика
- •Неопределённый и определённый интегралы Теоретические вопросы
- •Исследование функции методами дифференциального исчисления и построение её графика Теоретические вопросы
- •Задачи и примеры Часть 2
- •Решение типовых примеров.
- •Неопределённый и определённый интегралы Теоретические вопросы
- •Задачи и примеры Часть 3
- •Решение типовых примеров.
- •Задачи и примеры Часть 4
- •Решение типовых примеров
- •Тема 1. Дифференциальное исчисление функции одной переменной……… … …2
- •Тема 2. Неопределённый и определённый интегралы………………… ………… 12
- •Дифференциальное исчисление функции одной переменной
- •Исследование функции методами дифференциального исчисления и построение её графика
- •Неопределённый и определённый интегралы Теоретические вопросы
Решение типовых примеров.
Найти неопределённые интегралы. Проверить результат дифференцированием (в одном из примеров).
а)
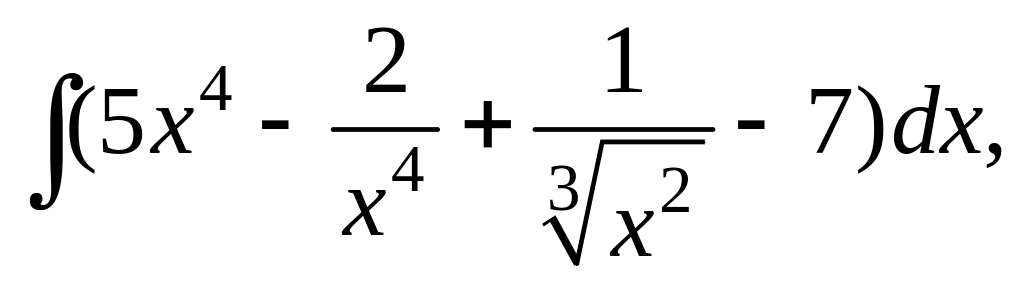 б)
б)
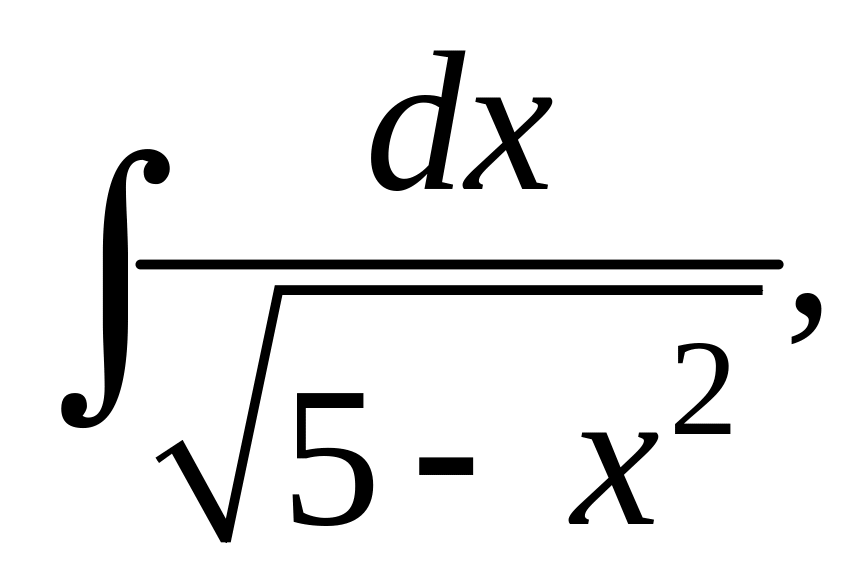
в)
![]() г)
г)
![]()
д)
![]() е)
е)
![]()
Решение.
а)

=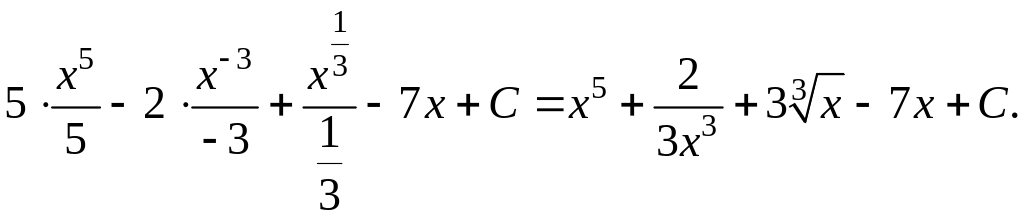
б)
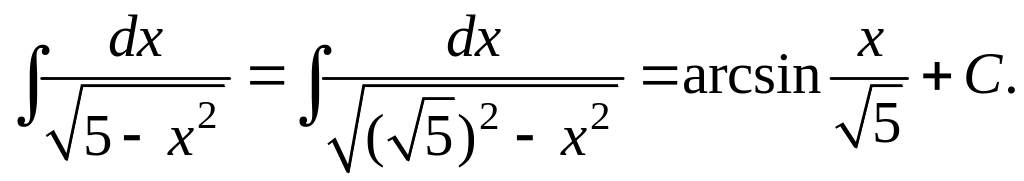
в)
![]()
Нужно использовать формулу
интегрирования по частям:
![]()
Для этого обозначим
![]()
![]() тогда
тогда
![]()
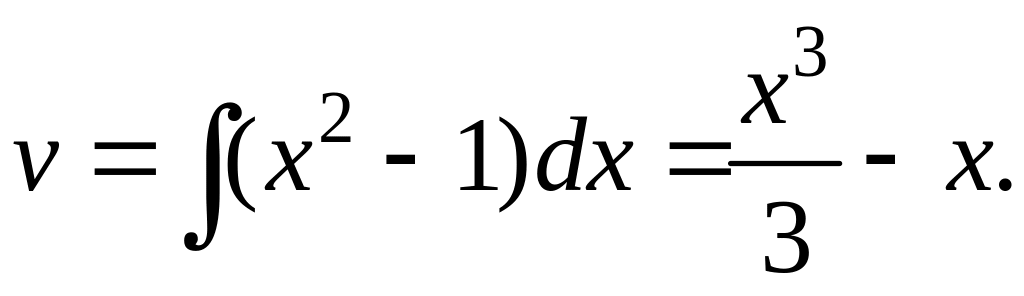
Тогда, применяя формулу интегрирования по частям, получим
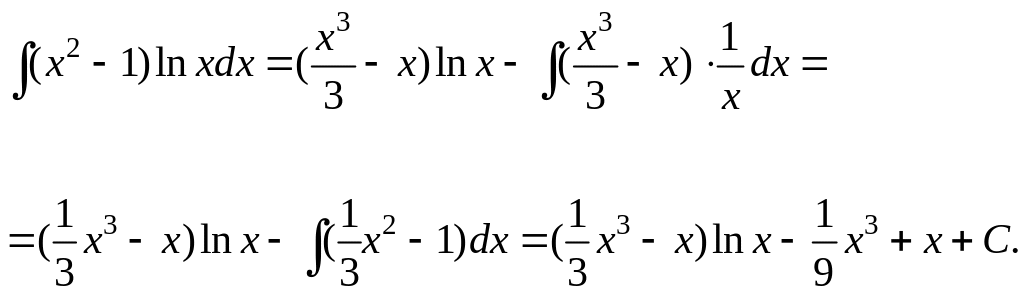
г)
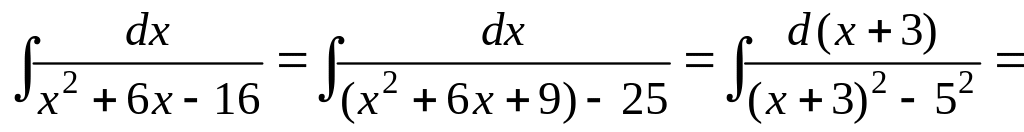
![]()

д)
![]()
![]()
![]()
Использована формула:
![]() .
е)
.
е)

![]()
Проверим результат интегрирования в примере д) дифференцированием:
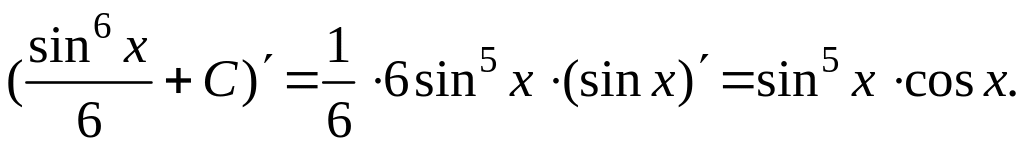
Получили подынтегральную функцию. Следовательно, интеграл нашли верно.
Задачи и примеры Часть 4
В задачах 1 4 найти с помощью определённых интегралов
1) Площадь плоской фигуры, расположенной в первом квадранте и ограниченной заданными параболой, прямой и осью ОХ;
2) Объём тела, образованного вращением вокруг оси ОХ данной плоской фигуры.
1.
![]()
![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]()
![]()
Решение типовых примеров
Пример 1. Найти с помощью
определённого интеграла площадь плоской
фигуры, расположенной в первом квадранте
и ограниченной параболой
![]() прямой
прямой
![]() и осью OX ( рис.3
).
и осью OX ( рис.3
).
Решение. Сделаем чертёж: в
осях ХОУ построим параболу
![]() и прямую
и заштрихуем искомую площадь, расположенную
в первом квадранте. Затем найдём абсциссу
точки пересечения параболы и прямой в
первом квадранте. Для этого приравняем
правые части уравнений параболы
и прямой
и решим полученное квадратное уравнение
и прямую
и заштрихуем искомую площадь, расположенную
в первом квадранте. Затем найдём абсциссу
точки пересечения параболы и прямой в
первом квадранте. Для этого приравняем
правые части уравнений параболы
и прямой
и решим полученное квадратное уравнение
![]() или
или
![]() Корни этого уравнения
Корни этого уравнения
![]()
![]() Первому квадранту соответствует корень
Первому квадранту соответствует корень
Найдём абсциссу точки пересечения
прямой
с осью ОХ
![]() Решим уравнение
Решим уравнение
![]() ,
откуда
,
откуда
![]()
Искомая площадь фигуры
![]() где
где
![]() площадь фигуры, ограниченной данной
параболой
,
вертикальной прямой
площадь фигуры, ограниченной данной
параболой
,
вертикальной прямой
![]() и осью ОХ ;
и осью ОХ ;
![]() площадь фигуры, ограниченной вертикальной
прямой
площадь фигуры, ограниченной вертикальной
прямой
![]() данной прямой
и осью ОХ . Вычислим искомые площади:
данной прямой
и осью ОХ . Вычислим искомые площади:
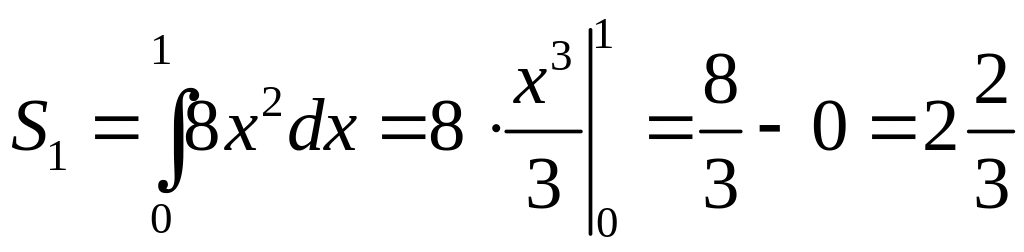 (кв.ед.)
(кв.ед.)
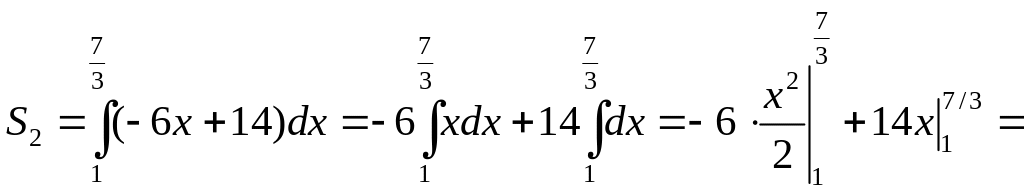
![]() (кв.ед.)
(кв.ед.)
Общая площадь
![]() (кв.ед.)
(кв.ед.)
Пример 2. Найти с помощью определённого интеграла объём тела, образованного вращением вокруг оси ОХ фигуры, расположенной в первом квадранте и ограниченной параболой прямой и осью ОХ (рис.3).
Решение. Можно считать, что тело
вращения ограничено при
![]() поверхностью, образованной вращением
параболы
вокруг оси ОХ , а при
поверхностью, образованной вращением
параболы
вокруг оси ОХ , а при
![]() поверхностью, образованной вращением
прямой
вокруг оси ОХ .
поверхностью, образованной вращением
прямой
вокруг оси ОХ .
Таким образом, общий объём тела вращения будет складываться из двух объёмов:
![]() Вычислим эти объёмы по формулам:
Вычислим эти объёмы по формулам:
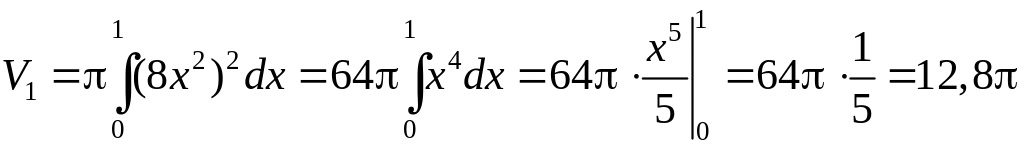 (куб.ед.)
(куб.ед.)
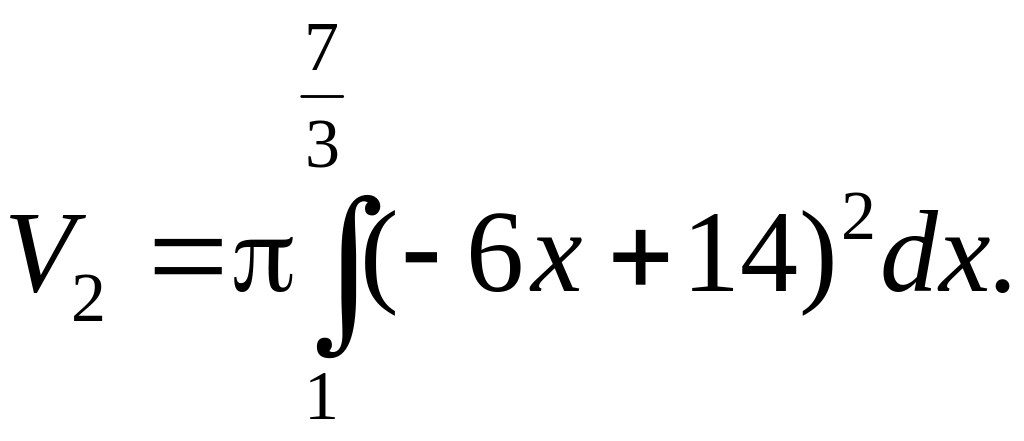
Для вычисления этого интеграла используем метод замены переменной.
Пусть
![]() Тогда
Тогда
![]() или
или
![]() отсюда
отсюда
![]() Определим новые пределы интегрирования,
соответствующие переменной
Определим новые пределы интегрирования,
соответствующие переменной
![]() :
при
:
при
![]() а при
а при
![]()
![]()
 (куб.ед.)
(куб.ед.)
![]() (куб.ед.)
(куб.ед.)
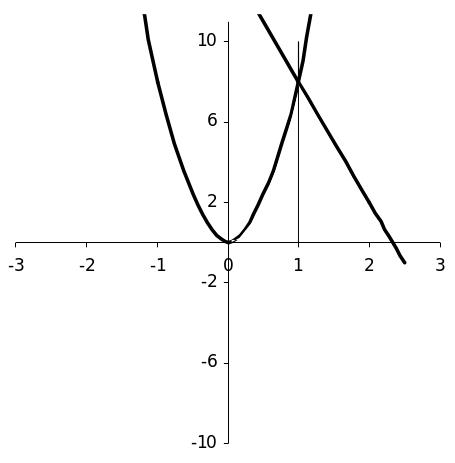
Рис. 3
Ответ : площадь плоской фигуры
![]() (кв. ед.),
(кв. ед.),
объём тела вращения
![]() (куб. ед.)
(куб. ед.)
С О Д Е Р Ж А Н И Е
