4.3. Вторая теорема двойственности

Пусть имеется симметричная пара двойственных задач

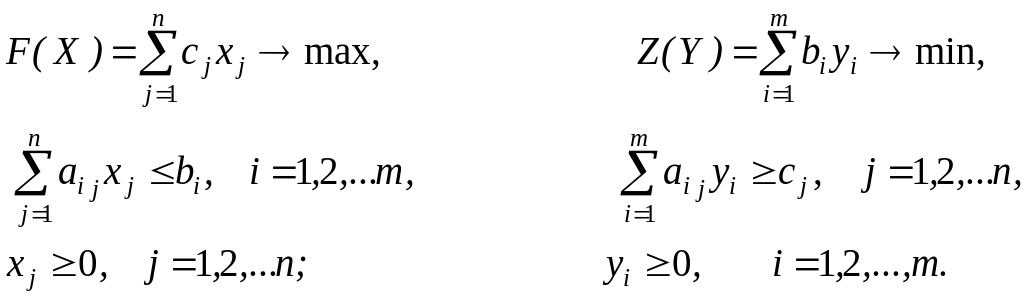
Теорема. Для того чтобы допустимые решения Х= (х₁, х₂, ..., х_п), Y=(y₁, y₂, ..., y_т) являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства:

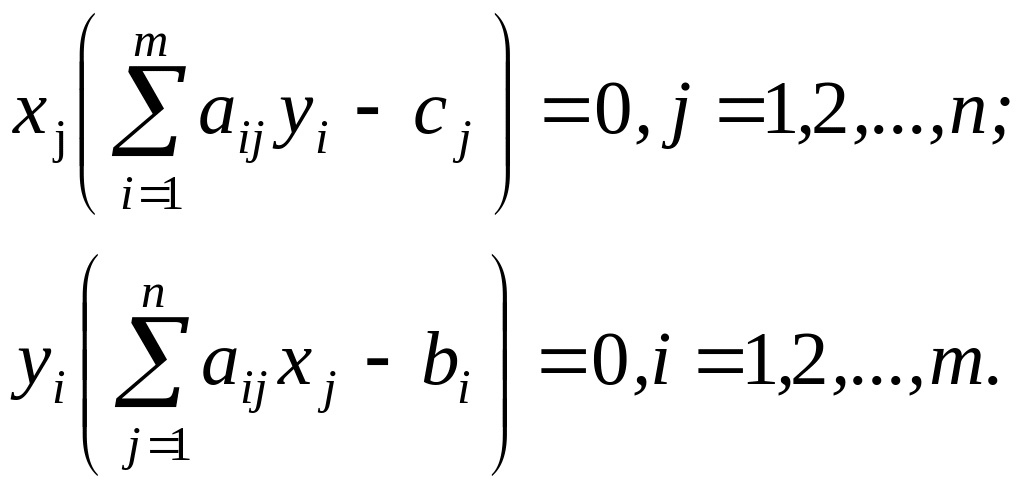
Пример 1. Для данной задачи составить двойственную, решить ее графическим методом и, используя вторую теорему двойственности, найти решение исходной задачи:

F(X) = -2x₁ + 2х₂ + 10х₃ + 4х₄ + 2х₅→ min,

Решение. Составим двойственную задачу: Z(Y) = 2у₁ + 3у₂→ max,

Р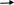 ешим эту задачу графическим методом. На рис. 4.1 изображены область допустимых решений задачи, нормаль п = (2, 3) линий уровня, линии уровня 2у₁ + 3у₂ = с и оптимальное решение задачи Y* = (3, 4).

Рис. 4.1.

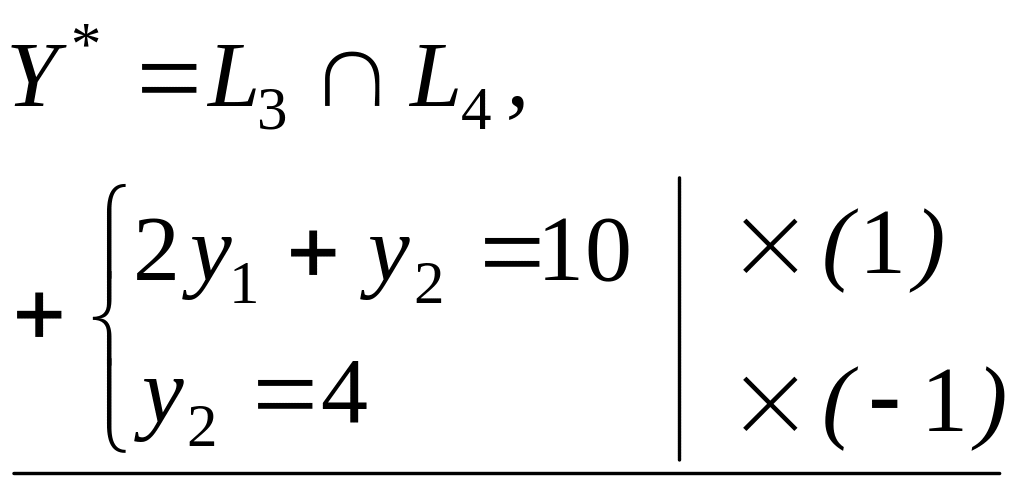
2у₁=6 у₁^*=3, у₂^*=4.

Y ^*=(3,4).

Z(Y ^*)=2·3+3·4=18.

Подставим оптимальное решение Y *= (3, 4) в систему ограничений. Получим, что первое, второе и пятое ограничения выполняются как строгие неравенства:

По второй теореме двойственности следует, что соответствующие координаты оптимального решения двойственной задачи, т.е. исходной задачи, равны нулю: х₁^* = х₂^* = х₅^*=0. Учитывая это, из системы ограничений исходной задачи получим

Отсюда находим х₃*= 1, х₄* = 2. Окончательно записываем X*=(0,0,1,2,0).

Ответ: min F(X) = 18 при X* = (0, 0, 1, 2, 0).

Пример 2. Для данной задачи составить двойственную, решить ее графическим методом и, используя вторую теорему двойственности, найти решение исходной задачи:

F(X) = 5x₁ + 3х₂ + 4х₃ -х₄ → max,

Решение. Составляем двойственную задачу Z(Y) =3y₁ + 3у₂→min,

Р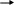 ешаем ее графическим методом (рис. 4.2). Для этого строим область допустимых решений (ОДР), нормаль п = (3, 3), линии уровня 3у₁ + 3у₂ = с. Перемещаем линии уровня до опорной прямой. Оптимальное решение (точку Y*) найдем, решая совместно уравнения прямых L₁ и L₂ соответствующих первому и третьему неравенствам.

Т аким образом, оптимальное решение Y*=(1,2), при котором minZ(Y)=9.

Рис. 4.2.

Используем вторую теорему двойственности. Подставляем координаты оптимального решения двойственной задачи Y* = (1, 2) в систему ограничений:

Второе и четвертое ограничения выполняются как строгие неравенства, следовательно, вторая и четвертая координаты оптимального решения исходной задачи равны нулю: х₂* = 0, х₄* = 0. Учитывая это, первую и третью координаты оптимального решения X* находим при совместном решении уравнений-ограничений:

3х₁ = 3 => х₁* = 1, х₃* = 1.

Ответ: max F(X) = 9 при X* = (1, 0, 1, 0). •

Задачи для самостоятельного решения

1. Составить и решить симплексным методом задачу, двойственную следующей: максимизировать функцию F =x₁+ x₂ +x₃ при ограничениях

2. Симплексным методом найти максимум функции F =x₁+ x₂ при ограничениях

Составить двойственную задачу и решить её симплексным методом.

3. Найти максимум функции F =2x₁-3 x₂ при ограничениях

Решить задачу симплексным методом, затем составить двойственную задачу и решить ее геометрически.

4. Найти минимум функции F =2x₁+4 x₂ при ограничениях

Решить задачу геометрически, затем составить двойственную задачу и решить ее симплексным методом.

Ответы: 1. Z _min = 4/3; 2. F _max = Z _min =9; 3. F _max =∞, двойственная задача не имеет решений; 4. F _min = Z _max =22.