2. Графический метод решения задач линейного программирования

2.1. Задача с двумя переменными

Пусть требуется найти максимальное значение функции

F(X) = с₁ х₁ + с₂ х₂

при ограничениях

Алгоритм решения ЗЛП с двумя переменными графическим методом:

1. Строится область допустимых решений.

2. Строится вектор 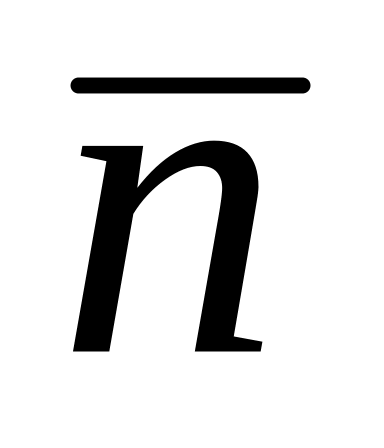= (с₁, с₂) с точкой приложения в начале координат.

3. Перпендикулярно вектору проводится одна из линий уровня, например линия уровня, соответствующая уравнению с₁х₁ + с₂х₂ = 0.

4.Линия уровня перемещается до положения опорной прямой. На этой прямой и будет находиться максимум или минимум функции.

Пример 1. Решить задачу линейного программирования графическим методом: F(X)=2x₁+4x₂→ max,

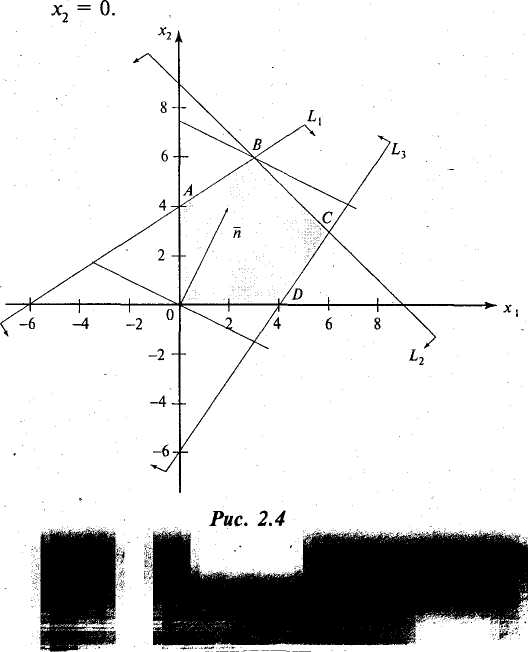
Решение. Изобразим на плоскости систему координат Ох₁х₂ и построим граничные прямые области допустимых решений (номера прямых соответствуют их порядковому номеру в системе). Область допустимых решений определяется многоугольником OABCD (рис. 2.1).

Для линий уровня 2х₁ + 4х₂ = с (с = const) строим нормальный вектор = (2, 4). Перпендикулярно вектору построим одну из линий уровня (на рис. 2.4 она проходит через начало координат). Так как задача на максимум, то перемещаем линию уровня в направлении вектора до опорной прямой.

Р

Рис. 2.1

В данном случае опорной прямой является прямая, проходящая через точку пересечения граничных прямых L₁ и L₂, т.е. через точку В = L₁∩L₂. Для определения координат точки В решаем систему уравнений

ешение. Изобразим на плоскости систему координат Ох₁х₂ и

Получаем х₁ = 3, х₂ = 6. Это и будет оптимальное решение данной задачи, которому соответствует максимальное значение целевой функции

max F(X) = 2 · 3 + 4 · 6 = 30.

Пример 2. Найти минимум функции F(X)=2x₁+x₂→ min при ограничениях

О

Рис. 2.2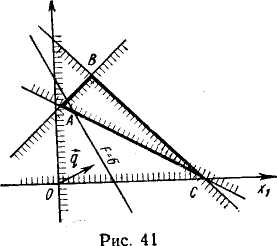

тличие этого примера от предыдущего состоит в том, что здесь ищется не максимум, а минимум функции F. Областью решений данной системы ограничений является треугольник АВС (рис.2.2). На рисунке изображены также исходная линия уровня и вектор q = (2; 1), показывающий направление движения этой линии для достижения максимума функции F. Так как требуется найти минимум этой функции, то будем передвигать исходную линию уровня в сторону, противоположную вектору q. Как видно из рис. 2.2, минимум функции F достигается в угловой точке А, координаты которой служат решением системы уравнений

Отсюда А (6/7; 25/7) и F_min = 37/7.

2.2. Графический метод решения задач линейного программирования с п переменными

Графическим методом можно решить ЗЛП, имеющие каноническую форму и удовлетворяющие условию n-r≤2, где п — число неизвестных системы; r — ранг системы векторов-условий (число линейно независимых уравнений системы).

Если уравнения системы ограничений линейно независимы, то r = т, где т — число уравнений.

Рассмотрим алгоритм метода на конкретном примере.

Пример. Решить графическим методом задачу

F(X)=x₁+x₂+5x₃+3x₄→ max,

Решение. Проверяем, применим ли графический метод при решении данной задачи. Нетрудно видеть, что любые два из векторов-условий, например линейно независимы, так как их координаты непропорциональны. Поэтому ранг системы векторов-условий r=2. Находим п- r= 4-2 = 2 ≤ 2. Следовательно, метод применим.

Приведем систему уравнений-ограничений к равносильной, с помощью линейных преобразований, предварительно записав её в матричной форме: .

Таким образом, получили систему: .

Выразим переменные х₁ и х₂: х₂=4-2х₃- х₄

х₁=9-2х₂ -3х₃-3х₄=9-2(4-2х₃- х₄)-3х₃-3х₄=9-8+4х₃+2х₄ -3х₃-3х₄=1+х₃- х₄

Т.к. х₁≥0 и х₂≥0, то систему уравнений мы записываем в виде системы неравенств: .

В результате получим эквивалентную задачу линейного программирования с двумя переменными, которая решается графическим методом

F(X)= 1+х₃- х₄+4-2х₃- х₄+5х₃+3х₄=5+4х₃+ х₄ → max

, х₃≥0, х₄≥0.

Изобразим на плоскости систему координат Ох₁х₂ и построим граничные прямые области допустимых решений. Находим оптимальное решение эквивалентной задачи и соответствующее ему максимальное значение целевой функции: С(2,0), F(C)=5+4·2+0=13.

Используем систему ограничений исходной задачи, приведенную к каноническому виду, и оптимальное решение задачи с двумя переменными для нахождения оптимального решения исходной задачи:

Р ис. 2.3

х₂=4-2х₃- х₄=4-2·2-0=0, х₁=1+х₃- х₄=1+2-0=3.

Следовательно, X=(3,0,2,0); F(X)=3+0+5·2+3·0=13.

Ответ: max F(X)= 13, при X=(3,0,2,0) .