Задачи для самостоятельного решения:
Задачи решить симплексным методом:
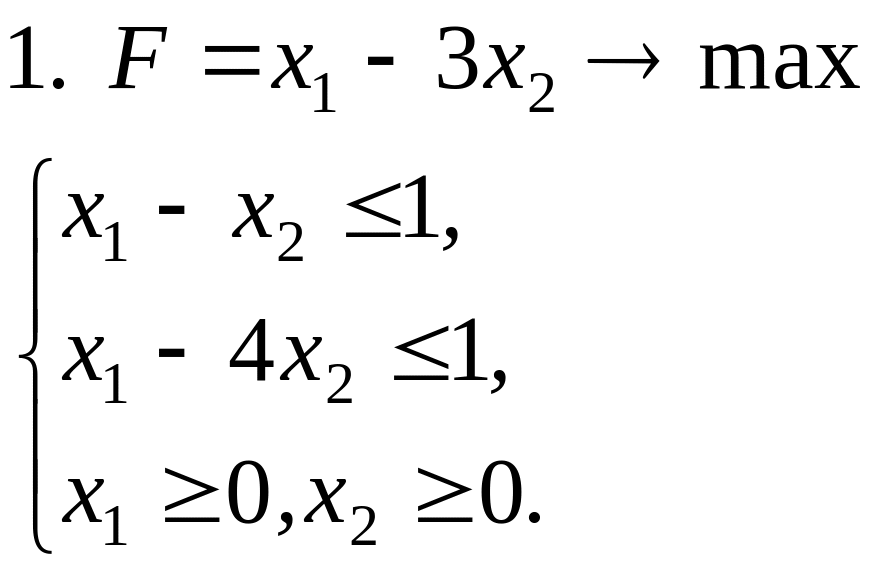
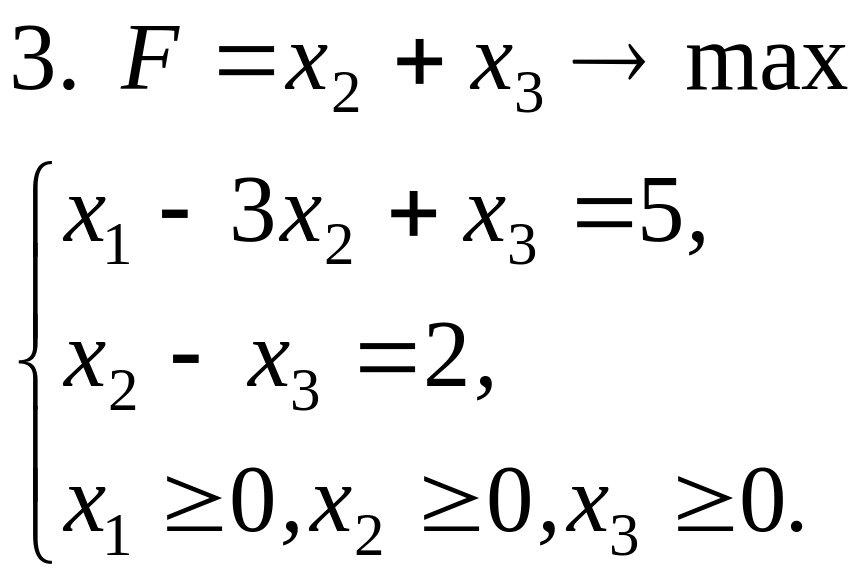
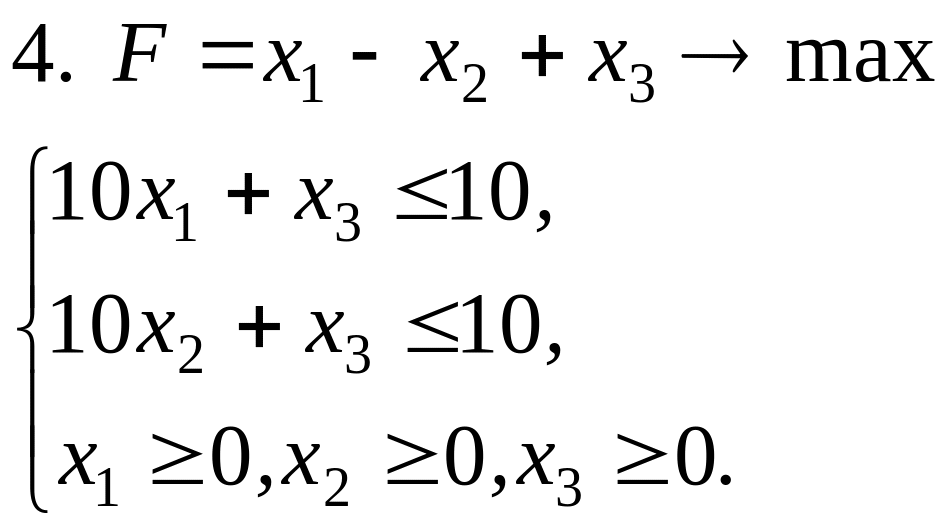
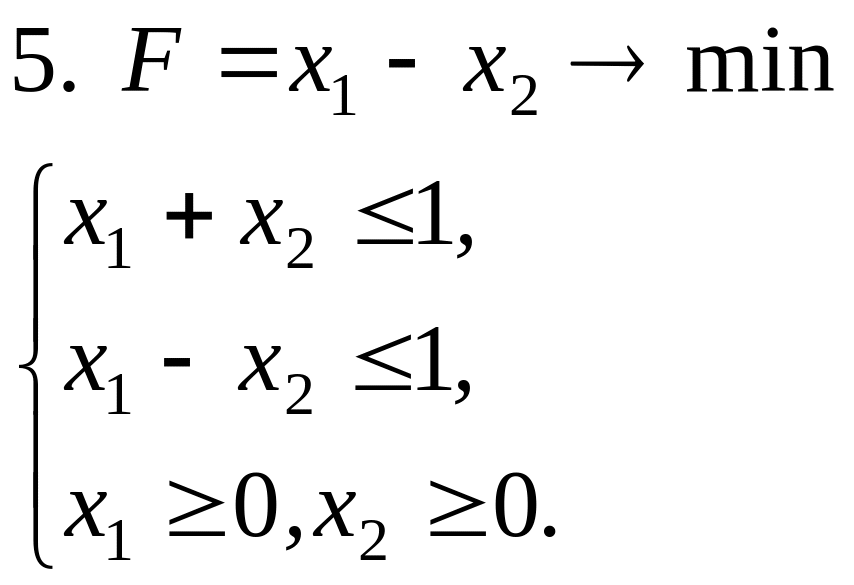
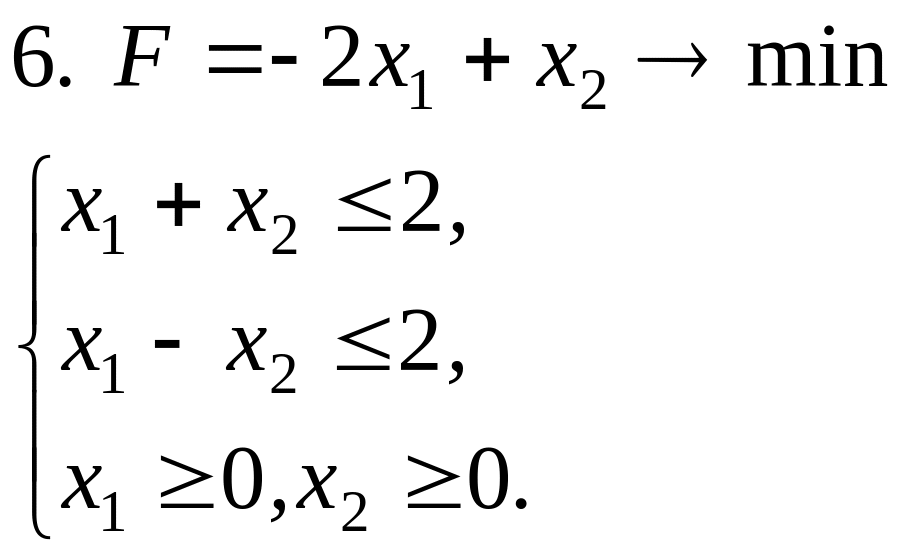
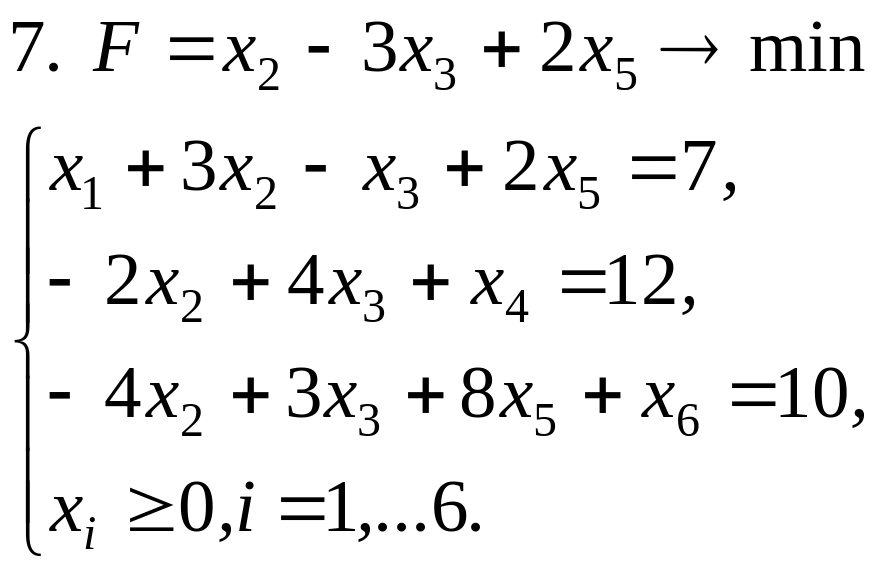
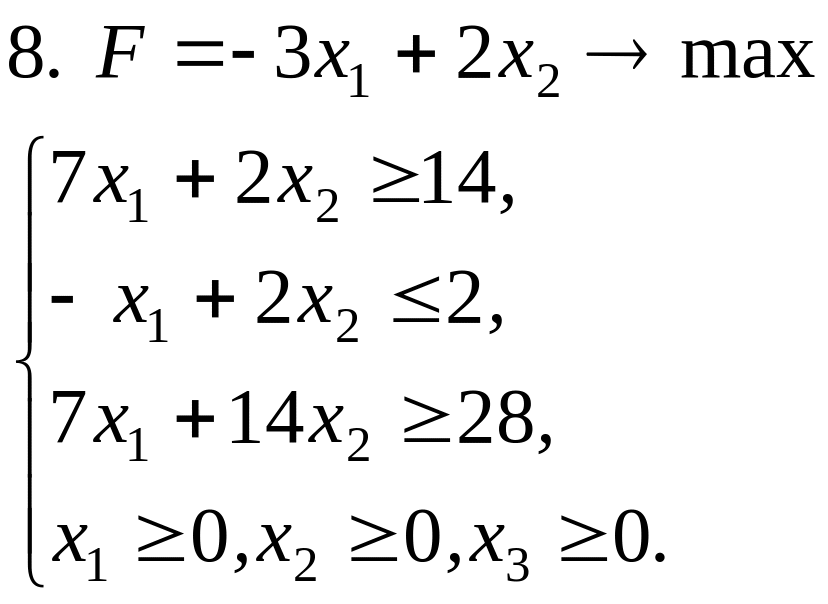
9. Кирпичный завод выпускает кирпичи двух марок (I и II). Для производства кирпича применяется глина трех видов (А, В и С). По месячному плану завод должен выпустить 10 усл. ед. кирпича марки I и 15 усл. ед. кирпича марки II. В табл. 3.3. указаны расход различных видов глины для производств 1 усл. ед. кирпича каждой марки и месячный запас глины. Какова наибольшая прибыль, если известно, что от реализации 1 усл. ед. кирпича марки I завод получает прибыль, равную 4 ден. ед., а марки II — 7 ден. ед.?
Таблица 3.3
Марка кирпича
|
Количество глины для производства 1 усл. ед. кирпича |
||
А |
В |
С |
|
I |
1 |
0 |
1 |
II |
0 |
2 |
2 |
Запасы глины, усл ед. |
15 |
36 |
47 |
10. Для производства стали определенной марки, в которую в качестве легирующих веществ должны входить химические элементы К, L, Р, можно закупать шихту двух видов (I и II). В табл. 3.4 указано, сколько требуется каждого из этих элементов для производства 100 т стали (по технологии можно немного больше, но меньше — нельзя). Содержание этих элементов в каждой тонне шихты, а также стоимость 1 т шихты каждого вида также приведены в таблице.
Таблица 3.4
Вид шихты
|
Стоимость 1 т шихты |
Легирующие вещества |
||
К |
L |
Р |
||
I |
3 |
3 |
2 |
1 |
II |
2 |
1 |
1 |
1 |
Необходимое количество легирующих веществ |
9 |
8 |
6 |
|
Определить наименьшие затраты для производства стали данной марки.
Ответы: 1. х1=1, х2=0, Fmax =1; 2. х1=12, х2=6, Fmax =84; 3. Задача не имеет решений, т.к. F не ограничена на области D сверху; 4. х1=х2=0, х3=10, Fmax =10; 5. х1=0, х2=1, Fmin =-1; 6. х1=2, х2=0, Fmin=-4; 7. х1=х4=х5=0, х2=4, х3=5, х6=11, Fmin=-11; 8. х1=3/2, х2=7/4, Fmax=-1; 9. Fmax=191 ден.ед.; 10. Fmin= 14 ден.ед.
4. Теория двойственности
4.1. Виды математических моделей двойственных задач
В теории двойственности используются четыре пары двойственных задач (приведем их в матричной форме записи):
Исходная задача Двойственная задача
Симметричные пары
1. F(X)=CX→max, Z(Y)=YA0→min
AX≤ A0 , YA≥ C,
X≥θ; Y≥θ.
2. F(X)=CX→min, Z(Y)=YA0→ max,
AX≥ A0 , YA≤ C,
X≥θ; Y≥θ.
Несимметричные пары
3. F(X)=CX→max, Z(Y)=YA0→min
AX= A0 , YA≥ C.
X≥θ;
2. F(X)=CX→min, Z(Y)=YA0→ max,
AX=A0 , YA≤ C.
X≥θ;
Здесь С=(с1, с2,…, сn), Y= (у1, у2,… …,ут),
Пример 1. Составить задачу, двойственную к данной
F(X) = х1 + 4х2 +3 х3→min,
Решение. Умножим первое ограничение-неравенство на -1. Задача примет вид исходной задачи симметричной пары двойственных задач:
F(X) = х1 + 4х2 +3 х3→min,
Умножим правые части ограничений на соответствующие переменные двойственной задачи и сложим их, получим целевую функции Z(Y) =
=-10у1 + 6у2 + 12у3→ max. Функция Z(Y) максимизируется, так как целевая функций исходной задачи минимизируется.
Умножаем коэффициенты при х1 на соответствующие переменные двойственной задачи и складываем их: -1у1 + 2у2 +1у3. Данная сумма меньше или равна коэффициенту при х1 в целевой функции -1у1 + 2у2 +1у3≤1.
Неравенство имеет вид « ≤», так как целевая функция двойственной задачи максимизируется. Аналогично составляются еще два ограничения двойственной задачи (соответствуют переменным х2, х3):
-1у1-1у2 + 2у3 ≤4, -1у1+3у3 ≤3.
Все переменные двойственной задачи удовлетворяют условию неотрицательности, потому что все ограничения исходной задачи - неравенства.
Окончательно двойственная задача имеет вид
Z(Y) = -10у1 + 6у2 + 12у3→ max,
Пример 2. Составить задачу, двойственную к данной
F(X) = х1 -х2 -2 х3+3 х4→min,
Решение. Данная задача имеет вид исходной задачи второй несимметричной пары двойственных задач. Запишем двойственную задачу
Z(Y) = 7у1 + 10у2 → max,
Переменные у1, у2 могут не удовлетворять условию неотрицательности, так как они соответствуют ограничениям-равенствам исходной задачи.
Пример 3. Составить задачу, двойственную к данной
F(X) = 3 - 2х1 + х3→min,
Решение. Используем общие правила составления двойственных задач. Умножим ограничения-неравенства на -1, так как в задаче на минимум они должны иметь вид «≥». Исходная задача запишется в виде
F(X) = 3 - 2х1 + х3→min,
Составим двойственную задачу: Z(Y) =3 - 3у1 + 5у2 - 8у3 + 6у4 → max,
Неизвестная у4, соответствующая ограничению-равенству, может быть любого знака.