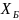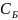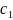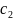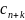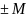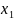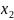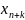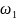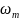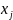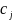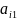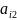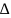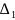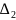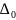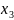- •Решение злп симплекс методом
- •1)Злп нужно привести к канонической форме
- •3) Сводят все данные в симплекс таблицу.
- •1)Все индексные оценки «хорошие», следовательно, получен оптимальный план. Если при этом решали м-задачу и все , то получен и оптимальный план исходной задачи.
- •3)Если есть «плохие» оценки, но в соответствующих столбцах нет ни одного положительного элемента, то целевая функция неограниченна.
Решение злп симплекс методом
1)Злп нужно привести к канонической форме
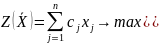
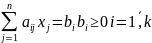
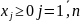
Для этого
а)во всех ограничениях
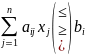
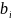 делают
неотрицательными. Т.е., если нужно,
умножают всю строку на (-1).
делают
неотрицательными. Т.е., если нужно,
умножают всю строку на (-1).
в)превращают неравенства в равенства, для чего вводят дополнительные переменные.
Если имелось неравенство
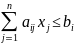
то
к левой части прибавляют неотрицательную
переменную
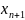 и получают уравнение
и получают уравнение
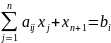
В целевую функцию эта переменная войдет с нулевым коэффициентом.
Если имелось неравенство

то из левой части вычитают неотрицательную переменную и получают уравнение
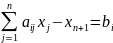
В целевую функцию эта переменная войдет с нулевым коэффициентом.
2)Выделяют
базисные переменные, т.е. такие, которые
входят только в одно уравнение с
коэффициентом (+1) и не входят в другие
уравнения. Если в уравнении такой
переменной нет, то добавляют искусственную
базисную переменную
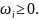 В целевую функцию эта переменная войдет
с коэффициентом +М, если решается задача
на минимум, и с коэффициентом (-М), если
решается задача на максимум. Здесь М –
большое положительное число. Получают
М – задачу.
В целевую функцию эта переменная войдет
с коэффициентом +М, если решается задача
на минимум, и с коэффициентом (-М), если
решается задача на максимум. Здесь М –
большое положительное число. Получают
М – задачу.
3) Сводят все данные в симплекс таблицу.
|
|
|
|
… |
|
|
… |
|
В |
|
|
… |
|
|
… |
|
|||
|
|
|
|
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
…. |
… |
|
|
|
… |
… |
… |
… |
… |
|
|
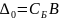 ,
,
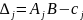 – индексные оценки.
– индексные оценки.
Пример.
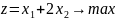
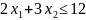
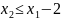
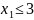
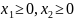
Перепишем
второе неравенство так, чтобы свободный
член был положительным:
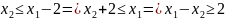
Получим систему ограничений:
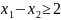
Превратим неравенства в равенства, для чего введем дополнительные переменные.


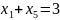
В целевую функцию эти переменные войдут с нулевыми коэффициентами.
Выделим базисные переменные, т.е. такие, которые входят только в одно уравнение с коэффициентом (+1) и не входят в другие уравнения.
Во
втором уравнении такой переменной нет,
поэтому добавим искусственную базисную
переменную
 в целевую функцию эта переменная войдет
с коэффициентом (-М), т.к. решается задача
на максимум. Получим М – задачу:
в целевую функцию эта переменная войдет
с коэффициентом (-М), т.к. решается задача
на максимум. Получим М – задачу:
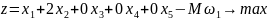
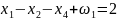
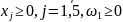
|
|
1 |
2 |
0 |
0 |
0 |
-M |
В |
|
|
|
|
|
|
|||
|
0 |
2 |
3 |
1 |
0 |
0 |
0 |
12 |
|
-M |
1 |
-1 |
0 |
-1 |
0 |
1 |
2 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
3 |
|
-M |
M |
0 |
M |
0 |
0 |
-2M |
|
-1 |
-2 |
0 |
0 |
0 |
0 |
0 |
||
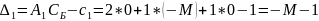
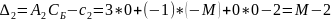
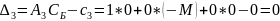

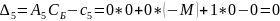
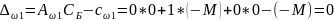
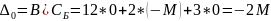
Если решают задачу на максимум, то «хорошими» считают неотрицательные индексные оценки.
Если на минимум, то – неположительные.
Если все оценки «хорошие», то полагают все свободные переменные (не входящие в базис) равными нулю, а все базисные – равными соответствующим свободным членам, и получают оптимальный план. При этом индексная оценка будет равна экстремальному значению целевой функции.
Если
есть «плохие» индексные оценки, то
«самая плохая» определит разрешающий
столбец
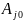 .
Если таких «самых плохих» равных друг
другу оценок несколько, то берут любой
из соответствующих столбцов.
.
Если таких «самых плохих» равных друг
другу оценок несколько, то берут любой
из соответствующих столбцов.
Затем в разрешающем столбце рассматривают все положительные коэффициенты и находят
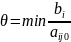
(это нужно чтобы в дальнейшем все свободные члены были неотрицательными).
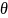 определяет разрешающую строку. Если
есть несколько равных
,
то берут любую соответствующую строку.
На пересечении разрешающей строки и
разрешающего столбца находится
разрешающий элемент
определяет разрешающую строку. Если
есть несколько равных
,
то берут любую соответствующую строку.
На пересечении разрешающей строки и
разрешающего столбца находится
разрешающий элемент
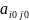 .
.
Затем из базиса выводят переменную, соответствующую разрешающей строке и вводят переменную, соответствующую разрешающему столбцу.
Все элементы разрешающей строки делят на разрешающий элемент.
В
столбцах базисных переменных все
элементы (включая индексные оценки)
равны нулю, кроме
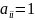 .
.
Остальные элементы находят по правилу прямоугольника:
Разрешающий элемент и искомый элемент создают главную диагональ прямоугольника.
Из произведения угловых элементов главной диагонали вычитают произведение угловых элементов вспомогательной диагонали, и результат делят на разрешающий элемент. Так же считают и индексные оценки (их считают двумя способами). И т.д.
В результате придем к одной из следующих ситуаций.