
- •Оглавление
- •Введение
- •Глава 1. Механика
- •Кинематика материально точки
- •1.1.2. Движение материальной точки по окружности
- •1.2. Динамика. Энергия и импульс
- •1.2.1. Динамика вращательного движения тела
- •1.3. Законы сохранения в механике
- •1.4. Закон всемирного тяготения. Движение материальной точки в поле силы тяжести Земли
- •1.5. Движение тел в неинерциальных системах отсчета. Силы инерции
- •1.6. Основы специальной теории относительности
- •Глава 2. Молекулярная физика. Термодинамика
- •2.1. Уравнение состояния идеального газа
- •2.2. Изотермический процесс
- •2.3. Изобарный процесс
- •2.4. Изохорный процесс
- •2.5. Барометрическая формула
- •2.6. Первое начало термодинамики. Адиабатный процесс
- •2.7. Второе начало термодинамики. Энтропия
- •2.8. Уравнение Ван-дер-Ваальса
- •Приложение некоторые сведения из разделов математики
1.1.2. Движение материальной точки по окружности
При движении материальной точки по окружности (рис. 2) можно описывать движение аналогично поступательному движению в декартовых координатах. Но поскольку окружность – кривая центрально симметричная, образованная вращением постоянного радиуса-вектора относительно его начала, то удобнее пользоваться полярными координатами с оговоркой того, что траектория движения – окружность радиуса R.
Переход от полярных координат к прямоугольным декартовым координатам производится согласно соотношению:
|
|
 y
y
![]() 2
2


 ,
,![]()
![]() 1
1


![]()

![]() x
x
Рис. 2. Пример плоского вращательного движения
Тогда,
для описания движения достаточно
фиксировать закон изменения угла
поворота со временем
![]() .
Углы поворота измеряются в радианах
([φ] – рад). Понятно, что угол поворота
величина векторная. Положительные
направления угла поворота принято
считать в направлении поворота от оси
x
к оси у
как показано на рис. 3.
.
Углы поворота измеряются в радианах
([φ] – рад). Понятно, что угол поворота
величина векторная. Положительные
направления угла поворота принято
считать в направлении поворота от оси
x
к оси у
как показано на рис. 3.
Аналогично поступательному движению определяется угловая скорость, как первая производная угла поворота по времени:
|
(3) |
Направление вектора угловой скорости выбирается по следующим правилам:
1) вектор угловой скорости лежит на оси вращения z;
2) направления вектора выбираем туда, куда закручивается правый винт по направлению движения тела (см. рис. 3).
В дальнейшем ось вращения всегда будет определяться как ось z.
z

![]()
![]()
![]()

O y
 x
x
Рис. 3. Пояснение к выбору направления угловых скоростей и ускорений
Если
в результате исследования обнаруживается,
что угловая скорость остается постоянной
(![]() ),
то движение тела по окружности называется
равномерным.
),
то движение тела по окружности называется
равномерным.
Для равномерного движения по окружности вводят понятия периода обращения тела по окружности и частоты (линейной) вращения. Периодом обращения тела по окружности (T) называют время одного полного оборота. Частотой вращения называют число оборотов за одну секунду, или величину обратную периоду:
|
(4) |
Размерность
периода обращения секунда ([T] – c),
а частоты – обратная секунда или Герц
([f]
– c–1=Гц).
Угловую скорость движения тела по
окружности, только при равномерном
движении, называют циклической частотой
вращения тела. Связь между линейной
частотой и циклической следующая:
![]() .
.
Аналогично поступательному движению определяют угловое ускорение, как первая производная угловой скорости по времени, или вторая производная от угла поворота по времени:
|
(5) |
Направление вектора углового ускорения определяется аналогично направлению угловой скорости (см. рис. 3). Если тело разгоняется, то угловое ускорение совпадает с угловой скоростью, а если тело тормозиться, то угловое ускорение направлено против угловой скорости (см. рис. 3).
Получим соотношения между линейными скоростями и ускорениями и угловыми. Линейная скорость связана с угловой соотношением:
|
(6) |
Его не трудно получить из определения скорости:
|
(7) |
Для
вывода формулы (7) достаточно рассмотреть
малое перемещение dS
от точки 1 к точке 2 (см. рис.2),которое
видно из начала координат под углом dφ.
Треугольник, образованный векторами
![]() прямоугольный,
так как вектор перемещения
,
образующий хорду окружности бесконечно
мал. Поэтому
прямоугольный,
так как вектор перемещения
,
образующий хорду окружности бесконечно
мал. Поэтому
![]() ,
как известно
,
как известно
![]() ,
поэтому
,
поэтому
![]() .
.
Для вывода формулы линейного ускорения продифференцируем формулу (6):
|
(8) |
Получили,
что полное ускорение определяется
суммой двух векторов
![]() и
и
![]() .
Рассмотрим, куда направлены эти вектора.
Вектор
направлен туда же куда и линейная
скорость, по касательной к окружности,
его называют тангенциальным ускорением
и обозначают
.
Рассмотрим, куда направлены эти вектора.
Вектор
направлен туда же куда и линейная
скорость, по касательной к окружности,
его называют тангенциальным ускорением
и обозначают
![]() .
Тангенциальным по тому, что направлен
по касательной к окружности, то есть
туда же куда и скорость. Второй вектор
.
Тангенциальным по тому, что направлен
по касательной к окружности, то есть
туда же куда и скорость. Второй вектор
![]() направлен к центру окружности, его
называют нормальным, радиальным или
центростремительным ускорением, и
обозначают
направлен к центру окружности, его
называют нормальным, радиальным или
центростремительным ускорением, и
обозначают
![]() .
По модулю нормальное и тангенциальное
ускорения равны произведению
соответствующих скаляров векторов,
входящих в векторные произведения:
.
По модулю нормальное и тангенциальное
ускорения равны произведению
соответствующих скаляров векторов,
входящих в векторные произведения:
|
(9) |

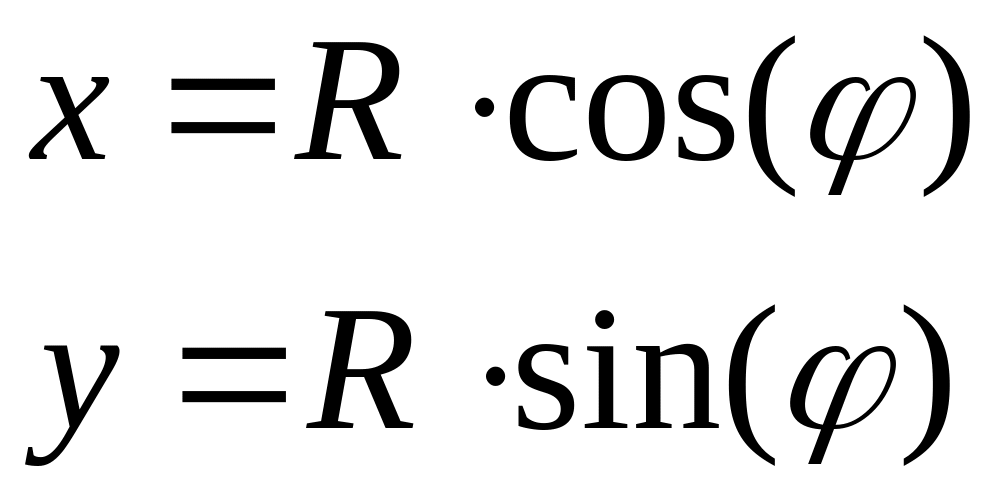 .
.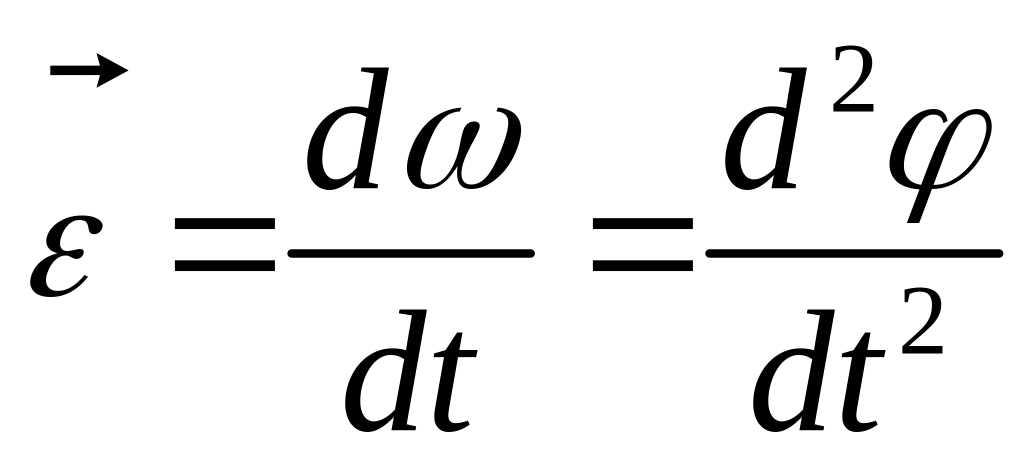 .
.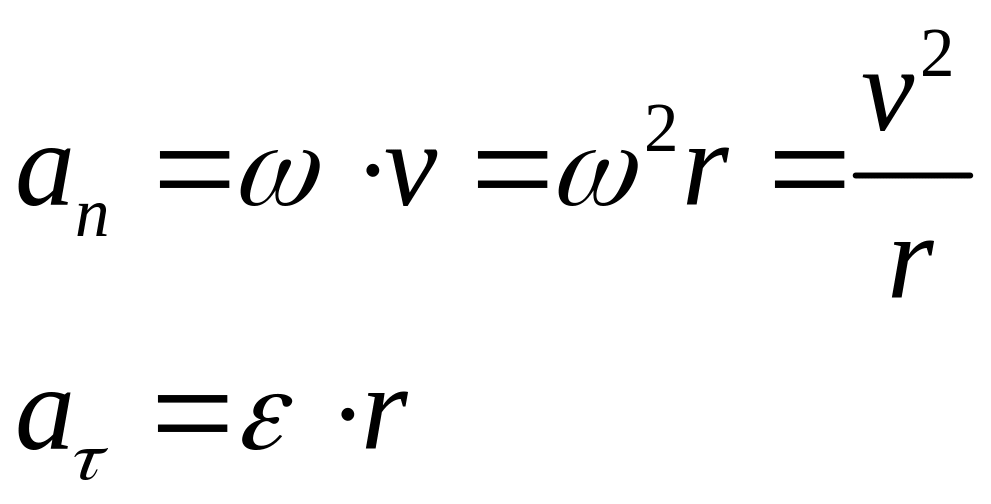 .
.