
- •1.1. Элементарные сведения о перестановках
- •1.2. Определители
- •1.2.1. Определитель n-ого порядка
- •1.2.3. Основные свойства определителей.
- •1.2.4. Умножение определителей.
- •1.2.5. Дифференцирование определителя.
- •1.3.1. Основные определения
- •1.3.2. Операции над матрицами
- •Тема 2. Элементарная теория погрешностей
- •2.1. Абсолютная и относительная погрешности
- •2.2. Основные источники погрешностей
- •2.3. Десятичная запись приближенных чисел. Значащая цифра. Число верных знаков
- •2.4. Округление чисел
- •2.5. Связь относительной погрешности приближенного числа с количеством верных знаков этого числа
- •2.6. Погрешность суммы
- •Очевидно, что
- •2.7. Погрешность разности
- •2.18. Понятие о погрешностях машинной арифметики
2.7. Погрешность разности
Рассмотрим разность двух приближенных чисел и=х1-х2. По формуле (2.14) предельная абсолютная погрешность и разности
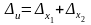 ,
,
т.е. предельная погрешность разности равна сумме предельных погрешностей уменьшаемого и вычитаемого.
Отсюда предельная относительная погрешность разности
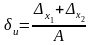 , (2.16)
, (2.16)
где А – точное значение абсолютной величины разности чисел х1 и х2.
Теорема. Относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел.
и=х1 х2… хп.
Ln u=lnx1+ lnx2+…+ lnxn.
Отсюда, используя приближенную формулу ln x d ln x = xn/x, находим:
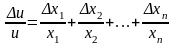 .
.
Оценивая последнее выражение по абсолютной величине, получим:
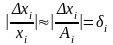 и
и
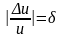 ,
,
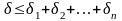 .
.
2.10. Погрешность частного
Теорема. Относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя.
Если и = х/у, то ln u = ln x – ln y и и/и = х/х - у/у.
Отсюда
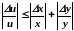 .
.
и =х+у
2.11. Число верных знаков частного
Пусть делимое х и делитель у имеют по меньшей мере т верных цифр. Если и - их первые значащие цифры, то за предельную относительную погрешность частного и может быть принята величина:
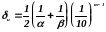 .
.
Отсюда получаем правило: 1) если 2 и 2, то частное и имеет по меньшей мере т-1 верных знаков; 2) если =1 или =1, то частное и заведомо имеет т-2 верных знака.
2.12. Относительная погрешность степени
Пусть и = хт (т – натуральное число), тогда ln и = т ln х и, следовательно,
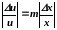 .
.
Отсюда
и = тх . (2.19)
т.е. предельная относительная погрешность т-й степени числа в т раз больше предельной относительной погрешности самого числа.
2.13. Относительная погрешность корня
Пусть теперь
 ,
тогда ит
= х. Отсюда
,
тогда ит
= х. Отсюда
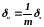 , (2.20)
, (2.20)
т.е. предельная относительная погрешность корня т-й степени в т раз меньше предельной относительной погрешности подкоренного числа.
1. Функции одной переменной. Абсолютная погрешность дифференцируемой функции y=f(x), вызываемая достаточно малой погрешностью аргумента х, оценивается величиной:
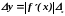 . (2.27)
. (2.27)
Если значения функции f(x) положительны, то для относительной погрешности имеет место оценка
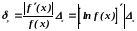 . (2.28)
. (2.28)
В частности, для основных элементарных функций получаем следующие правила.
а) Степенная функция y=xa. Абсолютная погрешность степенной функции равна:
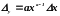 . (2.29)
. (2.29)
Относительная погрешность степенной функции равна:
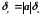 . (2.30)
. (2.30)
Например,
относительная погрешность квадрата x2
вдвое
больше относительной погрешности
основания х,
относительная погрешность
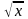 вдвое
меньше относительной погрешности
подкоренного числа х,
относительная погрешность обратной
величины 1/х
равна относительной погрешности самого
числа х.
вдвое
меньше относительной погрешности
подкоренного числа х,
относительная погрешность обратной
величины 1/х
равна относительной погрешности самого
числа х.
б) Показательная функция y=ах (a>0). Абсолютная погрешность показательной функции равна:
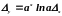 .
(2.31)
.
(2.31)
Относительная погрешность показательной функции равна:
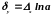 .
(2.32)
.
(2.32)
Заметим, что здесь относительная погрешность функции пропорциональна абсолютной погрешности аргумента.
Для функции y=ех отсюда получаем:
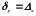 .
(2.33)
.
(2.33)
в) Логарифмическая функция y=ln x. Абсолютная погрешность натурального логарифма числа равна относительной погрешности самого числа:
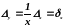 .
(2.34)
.
(2.34)
Для десятичного логарифма y=lg x имеем:
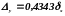 ,
(2.35)
,
(2.35)
откуда следует, что при расчетах с числами, имеющими т верных знаков, надо пользоваться (т+1)-значными таблицами логарифмов.
г) Тригонометрические функции. Абсолютные погрешности синуса и косинуса не превосходят абсолютных погрешностей аргумента:
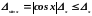 ,
,
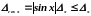 .
(2.36)
.
(2.36)
Абсолютные погрешности тангенса и котангенса всегда больше абсолютных погрешностей аргумента:
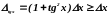 ,
, 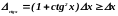 .
(2.37)
.
(2.37)
2.
Функции нескольких переменных.
Абсолютная погрешность дифференцируемой
функции y=f(x1,x2,…,
xn),
вызываемая достаточно малыми погрешностями
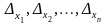 аргументов
x1,x2,…,
xn
оценивается
величиной
аргументов
x1,x2,…,
xn
оценивается
величиной
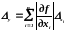 . (2.38)
. (2.38)
Если значения функции положительны, то для относительной погрешности имееи место оценка:
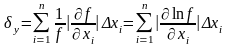 .
(2.39)
.
(2.39)
