1.2.3. Основные свойства определителей.

1. Если переменить местами строки и столбцы опреде­лителя, не меняя их порядка (иначе —транспонировав определитель), то определитель не меняется.

Следствие. Если известно какое-либо свойство определителя, относящееся к его строкам, то оно будет справедливо и по отношению к его столбцам. Поэтому в дальнейшем все свойства определителя будут даны по отношению к его строкам.

2. При перестановке двух строк определитель меняет знак.

3. Если все элементы какой-либо строки определителя равны нулю, то определитель равен нулю.

4. Общий множитель всех элементов строки опреде­лителя можно вынести за знак определителя.

5. Если все элементы некоторой строки определителя пропорциональны соответствующим элементам другой стро­ки, то определитель равен нулю.

6. Если все элементы i-й строки определителя пред­ставлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки, кроме i-й, такие же, как и в данном определителе, а j-я строка в первом определителе состоит из первых слагае­мых, во втором — из вторых слагаемых; это свойство распространяется на случай, когда каждый элемент i-и строки определителя есть сумма k слагаемых (k≥2).

7. Если к строке определителя прибавить линейную комбинацию нескольких других его строк (сумму произ­ведений на произвольные числа), то определитель не ме­няется.

8. Если одна из строк определителя есть линейная комбинация других его строк, то определитель равен нулю. Обратно, если определитель n-го порядка 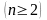равен нулю, то одна из его строк есть линейная комби­нация других строк.

9, Определитель равен сумме произведений всех элементов какой-либо его строки на их алгебраиче­ские дополнения:

.

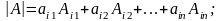
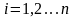10. Сумма произведений всех элементов какой-либо строки определителя на алгебраические дополнения соот­ветствующих элементов другой строки равна нулю:

.

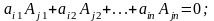
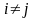1.2.4. Умножение определителей.

Произведение определителей и 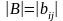одного и того же порядка n равно определителю 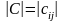того же порядка, где

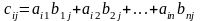
1.2.5. Дифференцирование определителя.

Если элементы a_ij определителя — дифференцируе­мые функции x, то

.

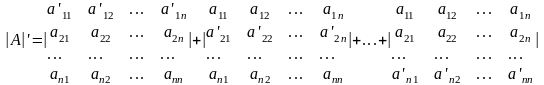1.3.1. Основные определения

Матрицей размера т x п называется прямо­угольная таблица чисел, расположенных в m строках и n столбцах

,

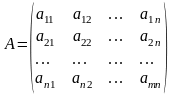числа a_ij (i=1, 2,…, m; j=1, 2,…, n) называются элементами матрицы А

1. Матрица-строка — прямоугольная матрица размера 1x n. Так как в этом случае матрица содержит только одну строку, то достаточно отмечать элементы одним индексом

.

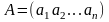2. Матрица-столбец — прямоугольная матрица размера m x 1

.

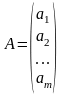3. Матрицу, состоящую из одного элемента, будем отождествлять с этим элементом

.

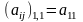4. Нулевая матрица — матрица, все элементы которой равны пулю. Будем обозначать нулевую матрицу 0.

5. Единичная матрица порядка n — квадратная мат­рица n-го порядка вида

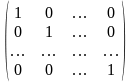или сокращенно

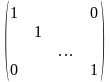
Единичную матрицу будем обозначать символом E. Используя символ Кронекера можно записать

. .

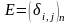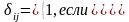
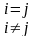6. Диагональная матрица n-ого порядка — квадратная матрица n-ого порядка, элементы которой 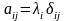, т. е. матрица вида .

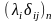В развернутой форме диагональная матрица запишется так:

, или .

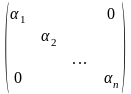Если 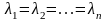матрица называется скалярной.

Одной из важнейших характеристик квадратной матрицы порядка n является ее определитель (или детерминант)

Очевидно, что detE=1, а определитель диагональной матрицы равен произведению диагональных элементов. Если detA отличен от нуля, то матрица называется не­вырожденной (или неособенной). В противном случае (если detA = 0) матрица А называется вырожденной (или осо­бенной).