3. Линейная парная регрессия

Линейная парная регрессия устанавливает взаимосвязь между:

Y = a + bx,

a, b – параметры модели;

y – показатель;

x – факторы;

.

. .

. . .

.

- теоретическое

Метод наименьших квадратов используется при построении парной регрессии и находи коэффициенты а и в при условии, что квадраты фактических отклонений и расчетные - минимальные.

- перейдем к средним величинам

Коэффициент кореляции

Зависимость между переменными х и у оценивается теснотой корреляционной зависимости.

Регрессионная зависимость зависит от единиц измерения. Чтобы перейти к безмерной оценке необходимо использовать среднеквадратичное отклонение.

(3)

Коэффициент корреляции:

(4)

(5)

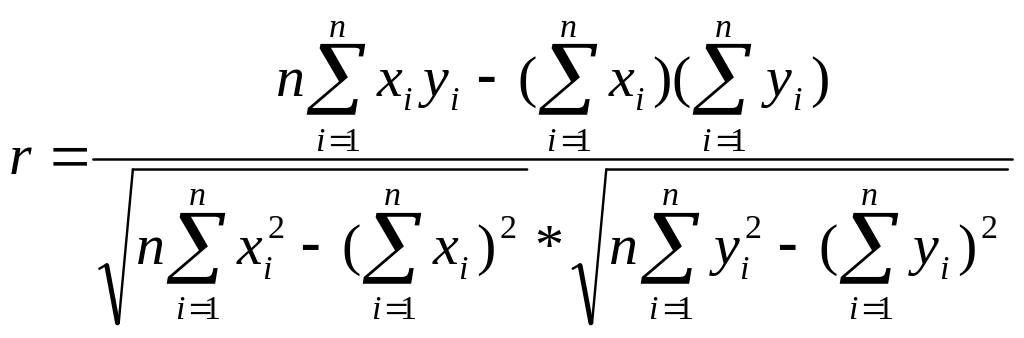
r = 0 → связи никакой нет

у

у

у

с увеличением х увеличивается у.

х

х

х

Оценка параметров регрессионной модели. Основные положения регрессионного анализа.

, где

- случайная переменная, характеризующая отклонение от линии регрессии.

Рассмотрим линейно-регрессионный анализ, для которого:

(1)

(2)

Предпосылки в линейно-регрессионном анализе состоят в следующем:

• В уравнении (2) величина есть неслучайная переменная, а есть случайная переменная;

• Математическое ожидание от случайной величины ,

(3), т.е. имеет место соотношение (1);

• Дисперсия (4) – условие гомоскедатичности или равноизменчивости возмущения;

• - возмущения некоррелированы, переменные - некоррелированы.

(5)

• Возмущение есть нормально распределенная случайная величина.

Если все эти предпосылки выполнены, то модель (2) называется классической нормальной линейной парной регрессионной моделью.

Для получения уравнения регрессии достаточно предпосылок (2,4). Условие (5) необходимо для оценки точности регрессии и ее параметров.

Параметрами модели являются свободный член а и коэффициент в.

Под действием неучтенных случайных факторов и ошибок наблюдения определяется с помощью остаточной дисперсии или дисперсии возмущения ошибок.

Несмещенная оценкой этой дисперсии называется выборочная дисперсия, которая определяется:

, где

- групповая средняя, найденная по уравнению регрессии;

- выборочная оценка возмущения или остаток регрессии;

- число степеней свободы;

n – число наблюдений;

2 – оцениваемые параметры;

составляет 10% от 403,66

S = 6,36 – 1,6% от

Интервальная оценка модели регрессии

* Доверительный интервал для функции регрессии .

Для условного материального ожидания с заданной надежностью доверительной вероятностью j = 1- неизвестное значение.

Найдем дисперсию групповой средней:

Уравнение регрессии через среднюю:

Построим эту модель геометрически: