Операторы Гамильтона и Лапласа.

Пусть мы имеем скалярную функцию , которая в каждой точке области определена и дифференцируема, и векторную функцию .

Рассмотрим «символический символ» - который называется оператором Гамильтона. Тогда многие характеристики полей удобно записывать так:

1) Градиент поля:

2) Дивергенция векторного поля :

3) Ротор векторного поля:

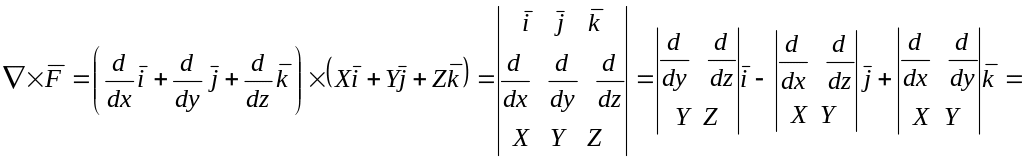
4) Потенциальное поле.

Векторное поле называется потенциальным, если есть градиент некоторой скалярной функции , то есть .

Для того, чтобы поле было потенциальным необходимо и достаточно, чтобы . То есть . Итак,

Доказательство:

Пусть поле потенциально, то есть или

Или , таким образом или .

5) Соленоидальное поле.

Векторное поле называется соленоидным или трубчатым, если , то есть векторное поле, в котором отсутствуют источники. В таком поле (то есть вихрей свободно от источников)

Итак,

Доказательство:

6) Оператор Лапласа.

Найдем (2)

Символ - Оператор Лапласа

Следовательно (2):

или , то есть

Заметим, что уравнение или называется уравнением Лапласа (функция, удовлетворяющая уравнению Лапласа, называется гармонической функцией).