Лекция13(II сем.)

Элементы теории поля.

Если в каждой точке части пространства определено значение некоторой величины, то говорят, что задано поле данной величины.

Скалярное поле. Векторное поле.

Определение:

Поле называется скалярным, если рассматривается величина, то есть характеризуется числовым значением.

Примером скалярного поля является поле плотности распределения массы неоднородного тела. Скалярное поле считается заданным, если определена скалярная функция . Геометрически его можно изобразить с помощью поверхностей уровня. Это совокупность точек поля, в каждой из которых скалярная величина принимает постоянное значение. Поверхности уровня определяются уравнением , где .

Пример 1

Найти поверхности уровня данного скалярного поля

Решение:

Область определения данного скалярного поля находится из неравенства , откуда . Это уравнение сферы с центром в начале координат и радиусом: .

Запишем уравнение поверхностей уровня:

, или ч, где .

Это семейство сфер с центром в начале координат, причем должно выполняться условие , .

Определение:

Векторным полем называется часть пространства, в каждой точке которого задана векторная величина (функция) .

В декартовой системе вектор можно разложить по базису , где - скалярные функции . Векторное поле, следовательно задается тремя скалярными функциями , и .

Для графического изображения векторного поля используются векторные линии.

Определение:

Векторной линией векторного поля называется кривая, в каждой точке которой касательная к ней совпадает с направлением векторного поля в точке касания.

Приведем примеры векторных полей:

Пример 1

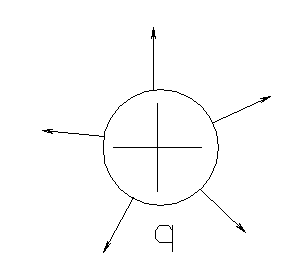
Электрическое поле . Каждой точке пространства ставится в соответствии вектор направленности , где - расстояние от точки поля заряда; - единичный вектор направления вектора, соединяющий заряд с точкой поля. Для положительного заряда векторными линиями будут лучи, выходящие из заряда.

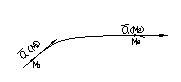
Пример 2

Рассмотрим поток несжимаемой жидкости, имеющей постоянную плоскость. Тогда вектор скорости жидкости определяет векторное поле. Он указывает направление в каждой точке, по которому стремится подвинуться частица жидкости, попавшая в эту точку.

Если поле скоростей с течением времени не меняется, то векторные линии будут служить траекториями жидких частиц и их называют линиями тока. Движение жидкости в этом случае называется стационарным.

Всякой дифференцируемой на области (то есть дифференциалу на скалярному полю) скалярной функции соответствует векторное поле ее градиентов

Уравнение касательной плоскости в точке к поверхности уровня скалярной функции , имеет вид:

где значения частных производных функции берутся в точке . Следовательно, в силу геометрического смысла коэффициентов уравнения плоскости, видно, что градиент перпендикулярен поверхности уровня плоскости, видно, что градиент перпендикулярен поверхности уровня функции .

Поток векторного поля.

Рассмотрим векторное поле, определенное векторной функцией , где функции , , непрерывны в некоторой области . Пусть - гладкая двухсторонняя поверхность, у которой выбрана сторона поверхности.

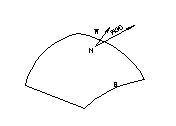
Определение:

Потоком П векторного поля через ориентированную поверхность называется поверхностный интеграл от скалярного произведения вектора и единичного вектора к этой поверхности:

Поток есть скалярная величина. Есть поверхность замкнутая, то обычно выбирается внешняя нормаль. Выясним физический смысл потока, если считать вектор вектором скорости несжимаемой жидкости, движущейся стационарно. В этом случае векторные линии являются линиями тока, и поток определяет объем жидкости, протекающей через поверхность в единицу времени. Если поверхность замкнутая, то поток вектора через нее дает разность между количествами жидкости, вытекающей из объема и втекающей в него в единицу времени.

Для вычисления потока надо найти единичный орт нормали к поверхности и свести нахождение поверхностного интеграла к вычислению двойного интеграла по проекции поверхности на одну из координатных плоскостей.

Пусть замкнутая поверхность взаимно однозначно проектируется в область плоскости . Тогда уравнение поверхности может быть задано в виде

или

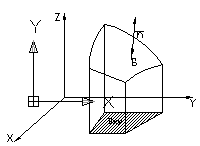
Известно, что вектор направлен перпендикулярно к поверхности, и поэтому вектор можно найти по формуле:

Где знак зависит от выбранной стороны поверхности.

Следовательно, направляющие косинусы вектора будут равны:

, ,

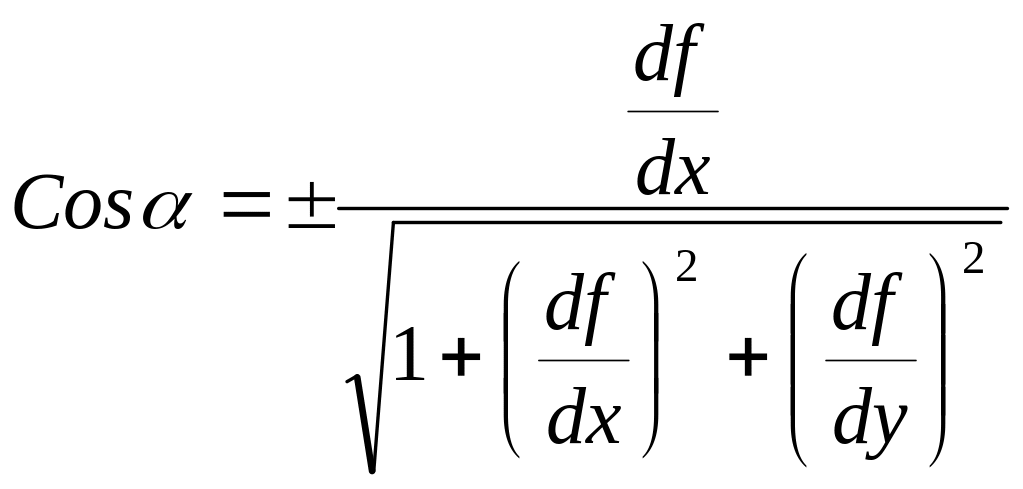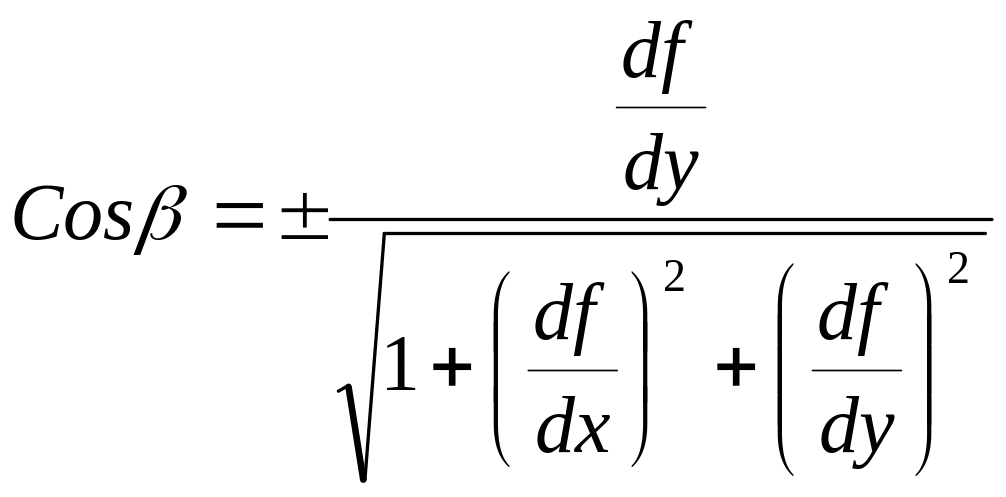Если , то в формулах берется знак + и, если , то знак -. Элемент площади этой поверхности с элементом площади проекции его связано формулой . Тогда по формуле:

Символ означает, что в подинтегральной функции вместо подставляется .

Если поверхность однозначно проектируется на плоскость или для вычисления потока пользуются аналогичными формулами:

,

где - проекция поверхности на плоскость , - проекция на плоскость .

Замечание 1 В случае, когда поверхность задана неявно уравнением . Единичный вектор нормали находится по формуле

где знак в правой части определяется выбором нормали поверхности .

Замечание 2 Если поверхность проектируется неоднозначно на координатную плоскость, то необходимо разбить ее на части так, чтобы для каждой из них выполнялось условие однозначности. тогда поток через всю поверхность можно представить в виде суммы через каждую поверхность в отдельности.