Ротор (вихрь) векторного поля.

Введем понятие ротора (вихря) векторного поля в точке .

Определение:

Вектор с проекциями на координатные оси называется ротором вектора

И обозначается символом :

Для удобства запоминания используем символический определитель

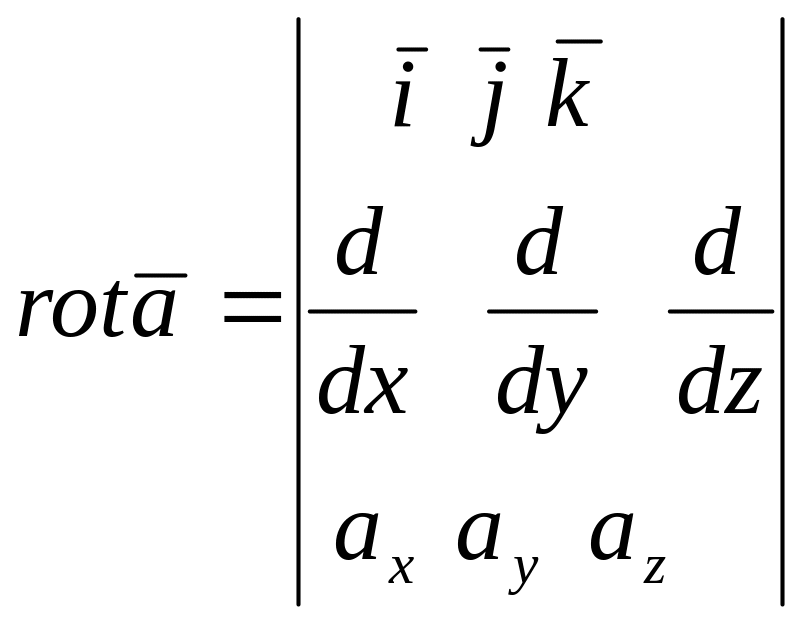
где операция умножения элементов второй строки на элементы третьей строки заменяется операцией дифференцирования.

Пример 3

Найти вихрь поля

Решение:

.

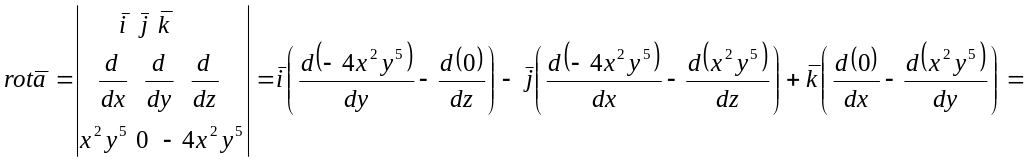
Теорема Стокса.

Теорема Стокса является одной из важных теорем теории поля. С помощью ее вычисления криволинейного интеграла по замкнутому контуру сводится к вычислению поверхностного интеграла по поверхности, натянутой на этот контур. Теорему Стокса особенно удобно использовать в том случае, если контур состоит из конечного числа дуг, каждая из которых имеет свое уравнение.

Теорема Стокса:

Циркуляция поля замкнутому контуру равна потоку вихря через любую поверхность , лежащую в векторном поле и имеющую своей границей контур :

.

При этом предполагается, что частные производные функции

на поверхности непрерывны, а направления на контуре выбирается так, что если смотреть с конца нормального вектора к поверхности , обход контура происходит против часовой стрелки.

Потенциальные и соленоидные поля.

Пусть дано векторное поле , где функции и их частные производные до второго порядка включительно непрерывны.

Определение:

Поле называется потенциальным, если существует скалярная функция такая, что выполняется условие .

Это векторное равенство трем скалярным равенствам: .

Функция , участвующая в определении, называется потенциальной функцией или потенциалом поля. Потенциал векторного поля определяется формулой:

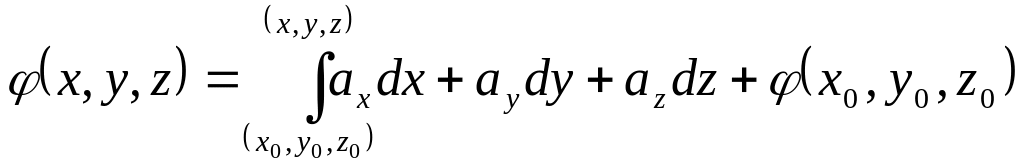где - некоторая физическая точка , - произвольная текущая точка. Вычислим ротор потенциального поля:

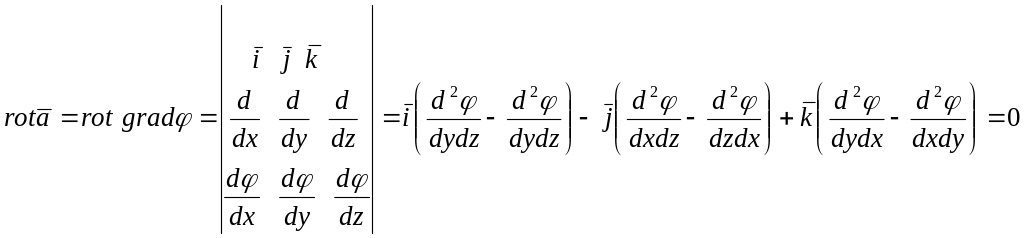
Получили, что потенциальное поле всегда безвихревое. Можно также доказать, что из равенства следует потенциальность поля. Сформулируем признак потенциальности поля: для того, чтобы поле было потенциальным, необходимо и достаточно, чтобы .

Свойство потенциального поля.

Потенциальное поле может быть задано одной скалярной функцией- его потенциалом, тогда как любое векторное поле требует задания трех скалярных функций- проекций вектора по оси координат.

Циркуляция в потенциальном поле по любому замкнутому контуру равна 0.

, так как

Если рассматривать вектор как вектор силы, действующей в потенциальном поле, то получим, что в данном поле работа по любому замкнутому контуру равна 0.

В потенциальном поле криволинейный интеграл не зависит от пути интегрирования и равен разности потенциальной функции в конечной и начальных точках этого пути:

.

Пример 4

Проверить, будет ли векторное поле потенцируем?

Решение:

Используем признак потенциального поля. Вычислим

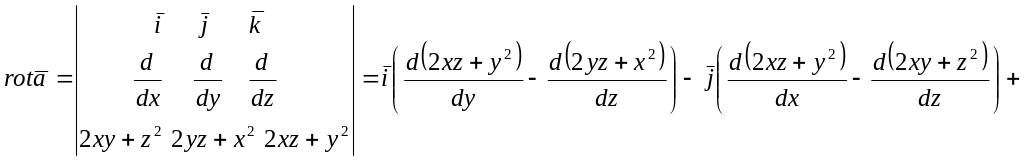
. Поле потенциальное.

Определение:

Непрерывное в области векторное поле называется соленоидным в этой области, если для любой ограниченной области с кусочно гладкой границей его поток через эту границу равен 0.

Теорема:

Для того, чтобы непрерывно дифференцируемое векторное поле было соленоидным в области , необходимо и достаточно, чтобы во всех точках области выполнялось: (1)

Доказательство:

1 Необходимость. Пусть поле - соленоидально в и точке . Так как точка - внутренняя для , то все достаточно малые по диаметру шары с центром в этой точке содержатся вместе с их границами в . В силу соленоидальности поля для этих шаров имеет место равенство: , а следовательно,

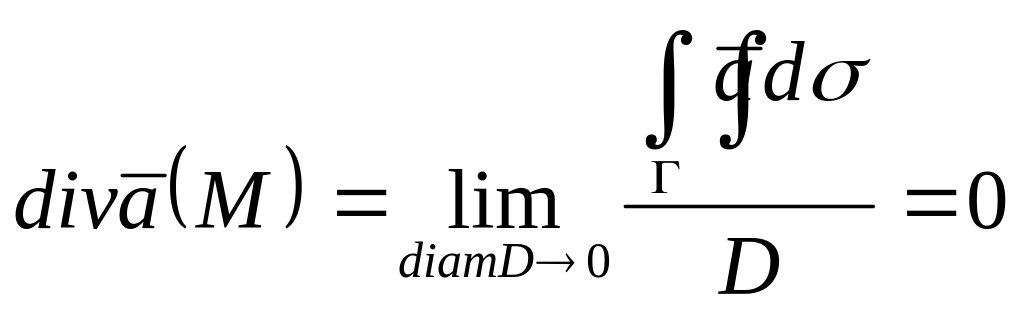
2 Достаточность. Если выполняется условие , то для любой области с кусочно гладкой границей в силу формулы Остроградского- Гаусса имеем: