
Лекция 9 (II сем.)
Интегральные операции в многомерных пространствах.
Кратные (двойные, тройные), криволинейные и поверхностные интегралы, как и обыкновенные (однократные) определенные интегралы, служат для вычисления различных величин. Все эти указанные интегралы определяются вполне аналогично и отличаются друг от друга в основном лишь областью интегрирования. Если вычисление однократного интеграла происходит на отрезке изменения одной переменной, то кратные, криволинейные и поверхностные интегралы рассматриваются в плоской области изменения двух переменных, или в пространственной области изменения трех переменных, или вдоль некоторой кривой, или по некоторой поверхности.
Двойной интеграл.
![]()
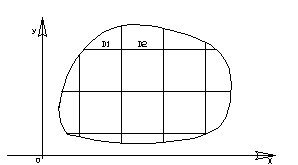
Пусть
![]() -
любая функция, непрерывная в некоторой
замкнутой области
-
любая функция, непрерывная в некоторой
замкнутой области
![]() плоскости
плоскости
![]() .
.
1) Разобьем область
произвольно на
![]() элементарных областей,
элементарных областей,
![]() не имеющих общих внутренних точек, и
обозначим их площади,
не имеющих общих внутренних точек, и
обозначим их площади,
![]() а диаметры через
а диаметры через
![]() (где
(где
![]() -
максимальное расстояние между двумя
точками на границе области
-
максимальное расстояние между двумя
точками на границе области
![]() ).
Пусть
).
Пусть
![]() -
наибольший из диаметров.
-
наибольший из диаметров.
2) Выберем в каждой
частичной области по произвольной точке
![]() и составим сумму вида:
и составим сумму вида:
![]()
![]() (1)
(1)
Где
![]() -
значение функции в точке
-
значение функции в точке
![]() и называется интегрируемой суммой
для функции
и называется интегрируемой суммой
для функции
![]() по области
.
по области
.
Интеграл Римана по квадрируемой области.
Определение:
Если существует
предел при
![]() интегральных сумм (1), то этот предел
называется интегралом Римана от
функции
интегральных сумм (1), то этот предел
называется интегралом Римана от
функции
![]() по области
и обозначается
по области
и обозначается
![]()
Какие же области
квадрируемы? Область
называется простой, если ее граница
состоит из конечного числа замкнутых
контуров
![]() каждой из которых является непрерывной
кусочно-гладкой замкнутой кривой, не
имеющей самопересечений. (Мы говорим,
что кривая
каждой из которых является непрерывной
кусочно-гладкой замкнутой кривой, не
имеющей самопересечений. (Мы говорим,
что кривая
![]() является кусочно-гладкой, если она
непрерывна и состоит из конечного числа
частей таких, что на каждой
является кусочно-гладкой, если она
непрерывна и состоит из конечного числа
частей таких, что на каждой
![]() -
уравнение кусочно-гладкой кривой, то
вектор
-
уравнение кусочно-гладкой кривой, то
вектор
![]() -
кусочно-непрерывен). Всякая простая
область квадрируема.
-
кусочно-непрерывен). Всякая простая
область квадрируема.
Интегрируемость непрерывных и кусочно-непрерывных функций.
Непрерывная и
ограниченная в замкнутой области
функция
![]() равномерно непрерывна в ней, то
есть для
равномерно непрерывна в ней, то
есть для
![]() ,
что для
,
что для
![]() точек
точек
![]() и
и
![]() ,
таких, что
,
таких, что
![]() выполняется:
выполняется:
![]()
Определение:
Функцию
![]() будем называть кусочно-непрерывной
в области
,
если область
можно разбить на конечное число частей
будем называть кусочно-непрерывной
в области
,
если область
можно разбить на конечное число частей
![]() таких, что в каждой открытой области
функция
будет равномерно непрерывной.
таких, что в каждой открытой области
функция
будет равномерно непрерывной.
Имеем следующее предположение: функция , кусочно-непрерывная в квадрируемой области , интегрируема по этой области.
Основные свойства двойных интегралов.
![]() Предположение,
сделанное выше есть простое следствие
следующего свойства интеграла Римана
по области
:
если функция
Предположение,
сделанное выше есть простое следствие
следующего свойства интеграла Римана
по области
:
если функция
![]() интегрируема в областях
интегрируема в областях
![]() и
и
![]() ,
то она интегрируема и в объединении
этих областей; при этом, если области
и
не имеют общих внутренних точек, то:
,
то она интегрируема и в объединении
этих областей; при этом, если области
и
не имеют общих внутренних точек, то:![]() .
.
![]() Двойной интеграл
от суммы функций равен сумме двойных
интегралов от всех слагаемых:
Двойной интеграл
от суммы функций равен сумме двойных
интегралов от всех слагаемых:
![]() .
.
![]() Постоянный
множитель можно выносить за знак двойного
интеграла:
Постоянный
множитель можно выносить за знак двойного
интеграла:
![]() .
.
Сведение интеграла по области к повторному.
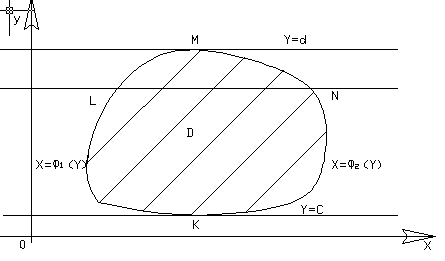
Пусть всякая прямая
параллельная оси
![]() и пересекающая область
,
имеет с ее границами не более двух общих
точек. Прямые
и пересекающая область
,
имеет с ее границами не более двух общих
точек. Прямые
![]() и
и
![]() касаются границ области в точке
касаются границ области в точке
![]() и
и
![]() граница разбивается на две линии
граница разбивается на две линии
![]() и
и
![]() ,
каждая из которых пересекается с любой
прямой, параллельной оси
,
каждая из которых пересекается с любой
прямой, параллельной оси
![]() ,
одной точке, тогда (такая область
называется стандартной (правильная)
относительно оси
,
одной точке, тогда (такая область
называется стандартной (правильная)
относительно оси
![]() ):
):
уравнение
![]()
уравнение
![]()
Выражение
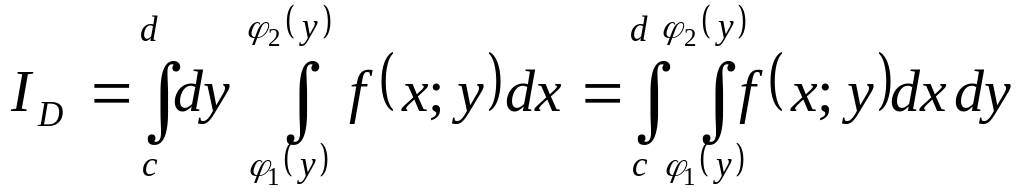 будем называть двойным интегралом
от функции
по области
.
будем называть двойным интегралом
от функции
по области
.
Если рассматривать
прямую
![]() пересекающую область
в точке входа
пересекающую область
в точке входа
![]() имеющую
ординату
имеющую
ординату
![]() в точке
в точке
![]() выхода, имеющую ординату
выхода, имеющую ординату
![]() тогда
тогда
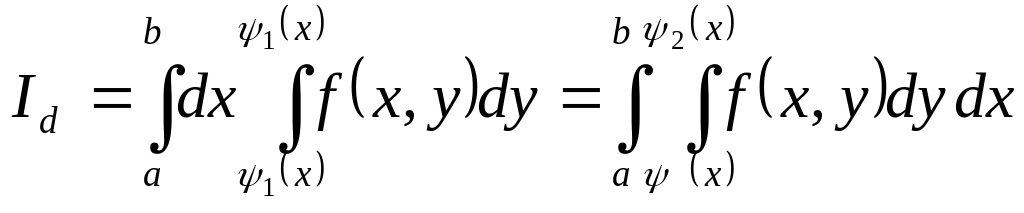 ,
где
,
где
![]() и
и
![]() -
соответственно наибольшие и наименьшие
значения переменной
-
соответственно наибольшие и наименьшие
значения переменной
![]()
Вычисления двукратного интеграла сводится к последовательному вычислению двух определенных интегралов, сначала вычисляется внутренний интеграл, считая одну из переменных постоянной, а результат интегрируется по внешней переменной.
Пример1.
Вычислить
![]()
Решение: Сначала
вычисляем внутренний интеграл, где
![]() является переменной, а
является переменной, а
![]() постоянная:
постоянная:
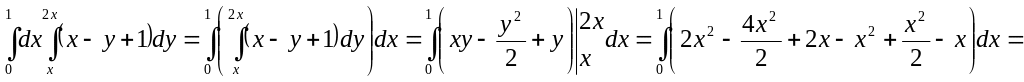
![]()
![]()
