Свойства двукратных интегралов.
Если стандартную
в направлении оси
область
разбить на две области
и
прямой, параллельной оси
или оси
,
то двукратный интеграл
по области
будет равен сумме таких же интегралов
по области
и
,
то есть:
(Оценка двукратного
интеграла). Пусть
и
-
наименьшее и наибольшее значение функции
в области
Обозначим
через
площадь
области
Тогда имеет место соотношение
(Теорема о среднем)
Двукратный интеграл
от непрерывной функции
по области
с площадью
равен произведению площади
на значение функции в некоторой точке
области
,
то есть:
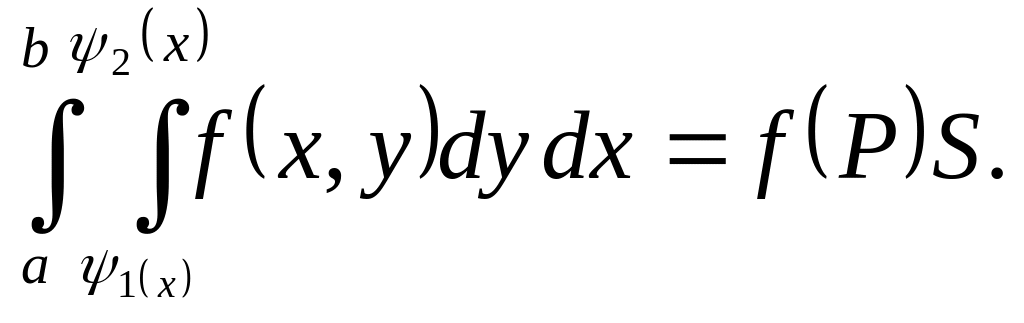
Теорема:
Двойной интеграл
от непрерывной функции
по стандартной области
равен двукратному интегралу от
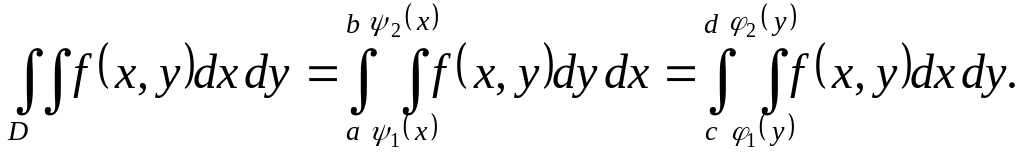
1) Область
разобьем прямыми, параллельными осям
координат на
правильных (прямоугольных) областей:
2) По свойству
:
(2)
3) По свойству
(теорема о среднем) каждое слагаемое
справа преобразуем:
4) Тогда (2) примет
вид:
,
где
-
некоторая точка области
Справа стоит
интегральная сумма для
по области
По теореме о существовании двойного
интеграла следует:
или
Изменение порядка интегрирования в двукратном интеграле.
Рассмотрим
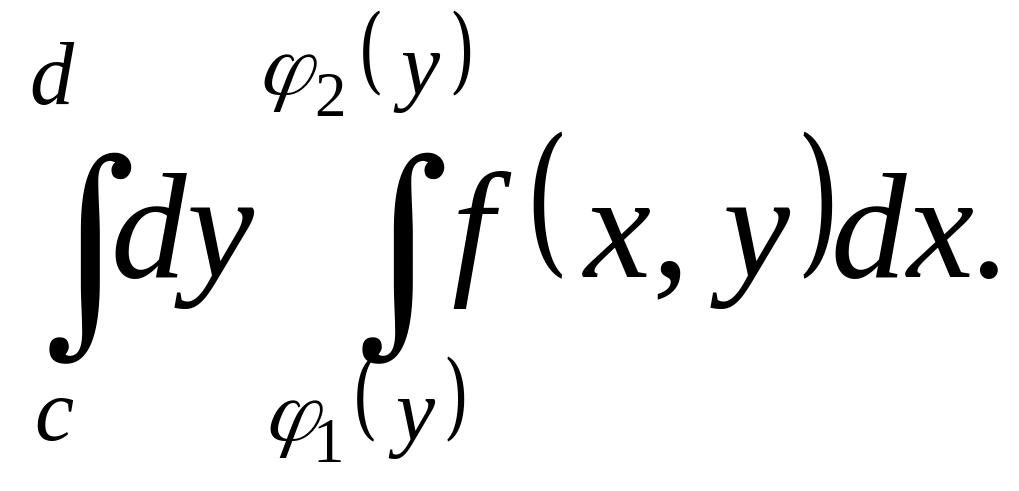
Изменение порядка
интегрирования означает преобразование
данного двукратного интеграла к такому,
в котором внутренний интеграл считается
по переменной
а внешний по
.Эту
задачу в некоторой степени можно считать
обратной для той, которая решалась
раньше. Там по заданной области
находились пределы интегрирования
двукратного интеграла. Здесь по пределам
двукратного интеграла следует восстановить
область
,
а затем записать двукратный интеграл
по
с другим порядком интегрирования.
Пример 2 Изменить
порядок интегрирования
.
Решение:
Здесь область
интегрирования ограничена прямыми
Она представляет собой трапецию.
При интегрировании
в другом порядке, вначале по
,
необходимо разбить область
прямой
,
параллельной
,
на две части, так как нижняя линия граница
этой области состоит из двух частей
и
,
которые имеют различные уравнения:
Вследствие этого и интеграл при изменении
порядка интегрирования будет равен
сумме двух интегралов:
Вычисление двойного интеграла сводится к последовательному вычислению двух обыкновенных определенных интегралов (двукратное интегрирование).
Геометрический смысл двойного интеграла.
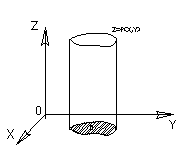
Пусть область
-
простая односвязная область на плоскости
.
Пусть
.
Геометрически
определяет объем цилиндрического тела,
в основании которого находится область
,
боковой поверхностью является
цилиндрическая поверхность, образующие
которой параллельны оси
,
которая сверху ограничена поверхностью
.
Замена переменных в двойном интеграле.
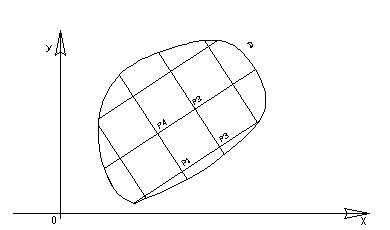
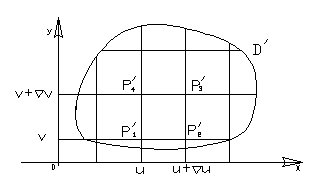
Пусть в плоскости
дана область D, ограниченная
линией L. Предположим, что
координаты
и
являются функциями новых переменных U
и V;
х =
,
=
(1)
Формулы (1)
устанавливают взаимно-однозначное
соответствие между точками области D
и
(
плоскость OUV).
Пусть в области D задана непрерывная функция z = f(x,y)
Каждому значению
функции z = f(x,y)
в области D соответствует
то же самое значение функции z
=F(U,V)
в области
,
где
Рассмотрим
интегральные суммы от функции
по области
.
Очевидно, имеет место следующее равенство:
(2)
Вычислим
,
то есть площадь криволинейного
четырехугольника
в плоскости
(Рис1).
Определим координаты его вершин:
(3)
При вычислении
площади криволинейного четырехугольника
будем считать линии
попарно параллельно прямыми; кроме того
приращения функций будем заменять
соответствующими дифференциалами.
Таким образом, мы будем пренебрегать
бесконечное множество
Тогда формулы (3) будут иметь вид:
(4)
При сделанных
допущениях криволинейный треугольный
четырехугольник
можно рассматривать как параллелограмм.
Его площадь
приближенно равна удвоенной площади
и находится по формуле аналитической
геометрии:
-
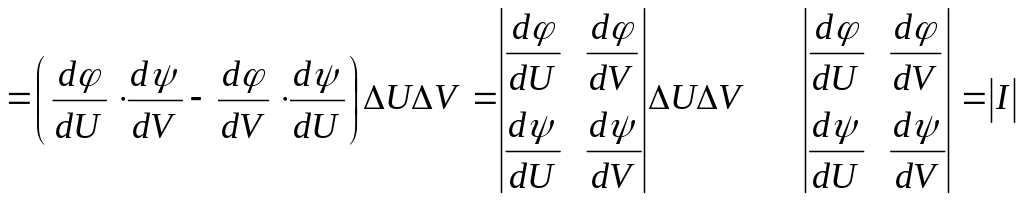функциональный определитель(Якобиан)
Тогда на основании
(2)
Переходя к пределу
при
получим
такое равенство:
(5)
Эта формула преобразования координат в двойном интеграле.