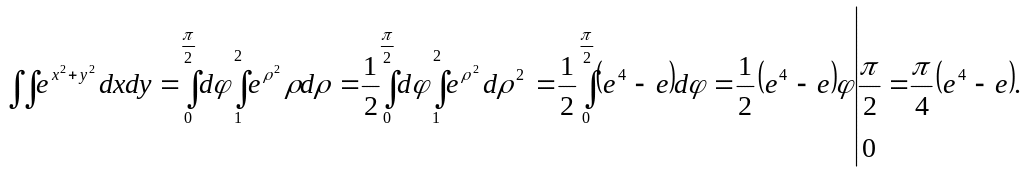Двойной интеграл в полярных координатах.
Декартова и полярная системы координат связаны следующими отношениями:
![]()
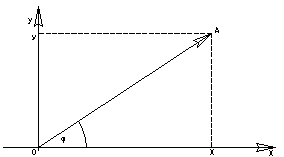
Где
![]() -
это радиус- вектор точки
-
это радиус- вектор точки
![]() -
угол, который образует радиус- вектор
с положительным направлением оси
(отсчет ведется против хода часовой
стрелки).
-
угол, который образует радиус- вектор
с положительным направлением оси
(отсчет ведется против хода часовой
стрелки).
Вычислим Якобиан преобразования декартовых координат в полярные
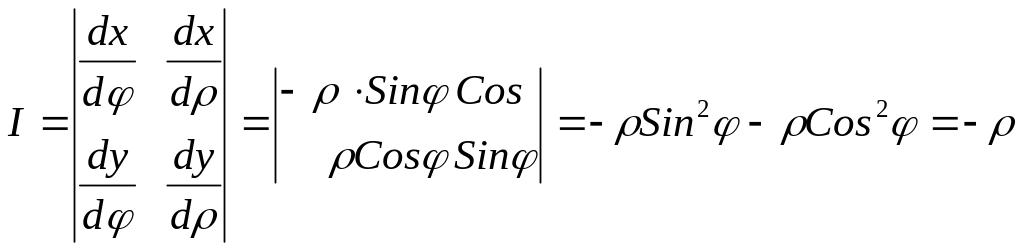
Следовательно,
![]()
Рассмотрим возможные
варианты областей
и
![]() .
Пусть, например,
ограничена двумя кривыми, полярные
уравнения которых
.
Пусть, например,
ограничена двумя кривыми, полярные
уравнения которых
![]() и
и
![]() непрерывные
функции, причем
непрерывные
функции, причем
![]()
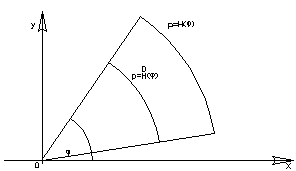
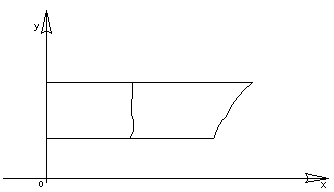
(Рис.3) (Рис.4)
и двумя полупрямыми,
выходящими из начала координат под
углами
![]() и
и
![]() к оси
к оси
![]()
Построим на
плоскости
![]() соответствующую область
соответствующую область
![]() .
.
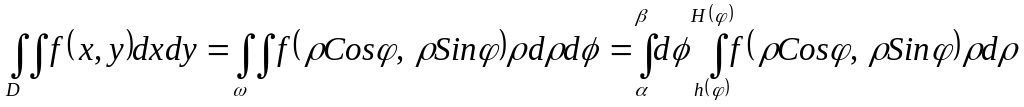
Те же пределы
можно получить с помощью Рис 3, рассуждая
так. У внешнего интеграла пределами
являются: наименьшее
![]() и наибольшее
значения полярного угла
и наибольшее
значения полярного угла
![]() для точек области
.
Для внутреннего интеграла имеем
для точек области
.
Для внутреннего интеграла имеем
![]() На
плоскости
точки, у которых
На
плоскости
точки, у которых
![]() располагаются на полупрямой, выходящей
из начала под углом
к оси
Так как полярная координата
располагаются на полупрямой, выходящей
из начала под углом
к оси
Так как полярная координата
![]() точки означает расстояния этой точки
от начала
точки означает расстояния этой точки
от начала
![]() ,
то нижний и верхний пределы внутреннего
интеграла равны соответственно расстоянию
от начала
самой близкой и самой далекой точки
области
,
то нижний и верхний пределы внутреннего
интеграла равны соответственно расстоянию
от начала
самой близкой и самой далекой точки
области
![]() лежащей на проведенном луче
.
Эти расстояния равны
лежащей на проведенном луче
.
Эти расстояния равны
![]() и
и
![]()
Аналогично в
случае области
,
ограниченной линиями, полярные уравнения
которых
![]() и
и
![]() где
где
![]() и
и
![]() непрерывные функции
,
непрерывные функции
,
![]()
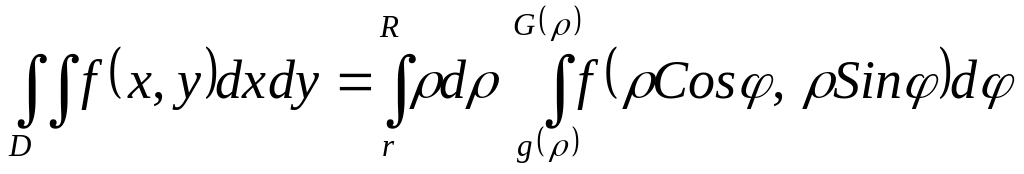
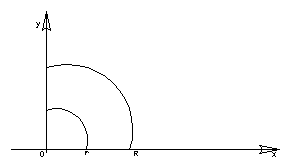
Вычислить интеграл
![]() по четверти кольца
по четверти кольца
![]() ,
лежащей в первом октанте.
,
лежащей в первом октанте.
Решение:

1) Изобразим область интегрирования.
2) Произведем замену
переменных по формулам
![]() .
.
3) Получаем
![]()
![]() часть
кольца в плоскости
часть
кольца в плоскости
![]()
Запишем уравнение границ области в полярной системе координат:
![]()
![]()
Угол
будет меняться в пределах от 0 до
![]()
Таким образом