Пример 4

Найти поток вектора через внешнюю сторону кругового косинуса, вершина которого находится в начале координат, радиус основания равен и высота равна (ось конуса направлена по оси ).

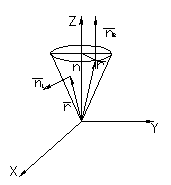
Решение:

Обозначим: - боковая поверхность косинуса

- основания конуса

Тогда .

Для боковой поверхности конуса вектор - радиус- вектор точки перпендикулярен вектору нормали . Следовательно, скалярное произведение и .

Вычислим поток через основание конуса. Для любой точки основания и вектор .За вектор т можно взять единичный орт .

Тогда . И поток

В результате имеем .

Дивергенция векторного поля. Вычисление потока через замкнутую поверхность.

Дано векторное поле . Найдем численную характеристику источника или стока поля в любой его точки . Окружим точку произвольной гладкой поверхностью вычислим поток поля через :

.

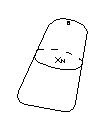
Разделим величину потока на объем тела , ограниченного поверхностью :

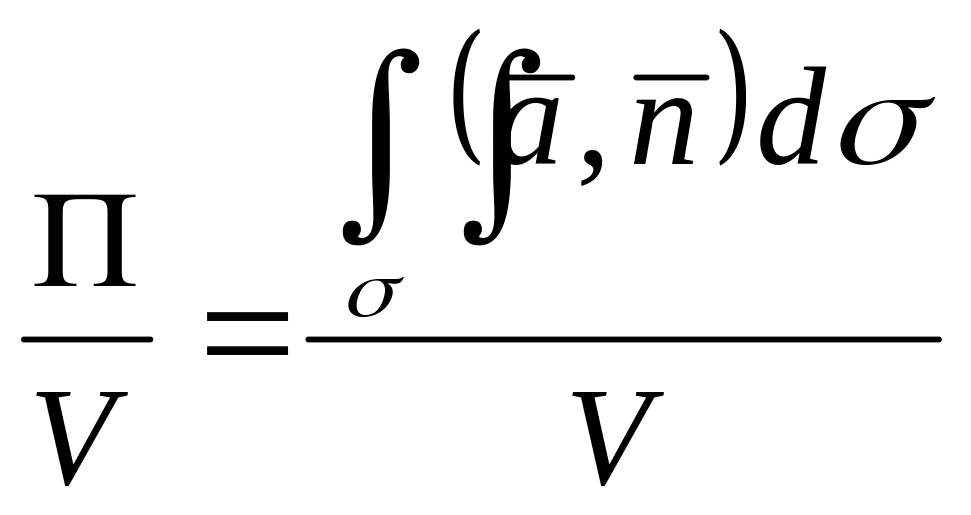
Получим среднюю плоскость источников и стоков, находящихся внутри поверхности . Перейдем к пределу при условии, сто диаметр области стремится к так, что поверхность стягивается в точке :

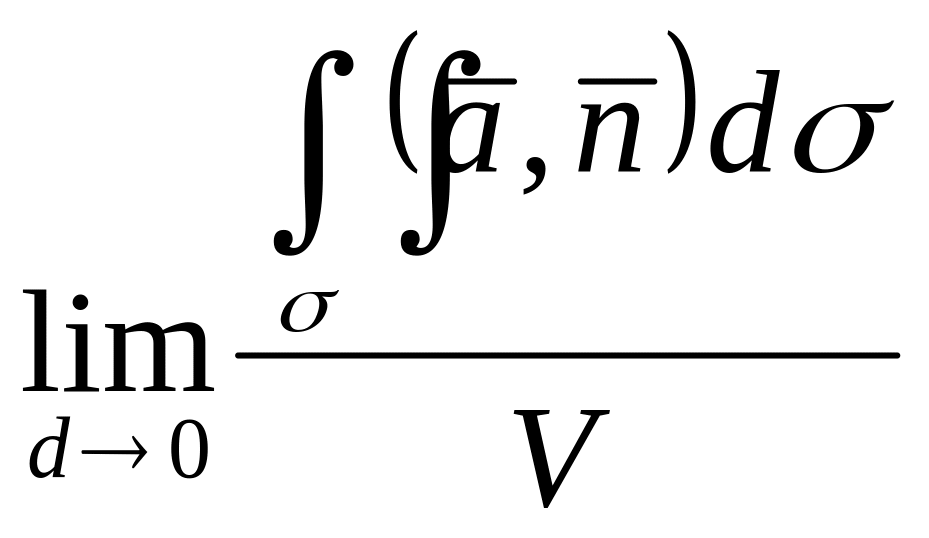
Данный предел, если существует, называется дивергенцией или расходимостью поля в точке

Дивергенция векторного поля есть скалярная величина, характеризующая плотность источника (стока) в точке .

Теорема:

Если проекции вектора непрерывны вместе со своими частными производными , то дивергенция поля существует и равна:

.

Векторное поле, в каждой точке которого дивергенция равна 0, называется соленоидальным. В данном поле нет ни источников, ни стоков. Векторные линии могут быть или замкнутыми, или уходить в бесконечность.

Пример 1

Найти дивергенцию поля в точке

Решение:

Запишем координаты векторного поля: , , . Вычислим частные производные:

Считаем их в точке

Находим дивергенцию поля в данной точке: . Получили, что в данной точке значит в ней находится источник поля.

Используя дивергенцию поля, с помощью теоремы Остроградского-Гаусса можно вычислить поток поля через замкнутую поверхность.

Теорема Остроградского-Гаусса

Пусть во всех точках и на его границе поле вектора определено и частные производные непрерывны. Тогда поток векторного поля через замкнутую поверхность равен тройному интегралу от дивергенции этого поля по объему , ограниченному поверхностью : .

Циркуляция векторного поля.

Пусть в области задано векторное поле , где функции и их частные производные непрерывны. В этой области возьмем кусочно-гладкую линию , где ,

Определение:

Криволинейным интегралом векторного поля вдоль линии называется интеграл вида (76)

Определение:

Циркуляцией векторного поля называют криволинейный интеграл, взятый по замкнутой линии

(77)

За положительное направление замкнутой кривой считают направление, при котором область, ограниченная этой кривой остается слева (обход против часовой стрелки). При изменении направления обхода контура циркуляция меняет знак.

Если - вектор силы, то циркуляция дает работу поля по перемещению точки вдоль замкнутого контура.

Запишем интеграл (77) в координатной форме. Вектор , вектор , их скалярное произведение . Тогда

, то есть имеем криволинейный интеграл второго рода.

Пример 2

Вычислить работу силового поля вдоль параболы от точки до точки

Решение:

Работа

.