§ 2.9. Связность.

§ 2.9.1. Степени связности графов

О рграф называется сильно связанным или сильным, если для любых двух его различных вершин x_i и x_j существует по крайней мере один путь, соединяющий x_i и x_j

О рграф называется односторонне связанным или односторонним, если для любых двух его различных вершин x_i и x_j существует по крайней мере один путь: из x_i в x_j или из x_j в x_i (или оба).

Орграф называется слабо связанным или слабым, если для любых двух его различных вершин x_i и x_j существует по крайней мере один маршрут, соединяющий x_i и x_j .

Если для некоторой пары вершин орграфа не существует маршрута, соединяющего их, то такой орграф называется несвязанным.

§ 2.9.2. Нахождение сильных компонент графа. Максимальный подграф.

М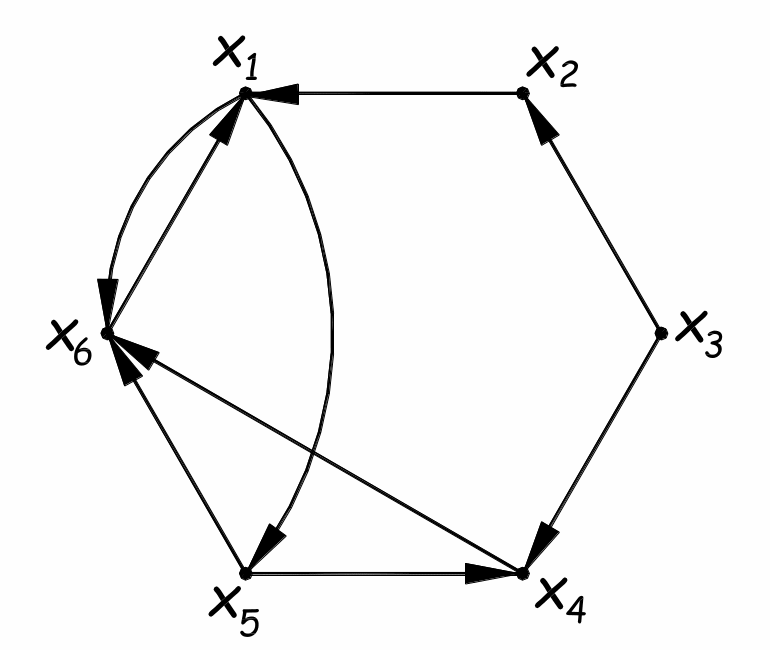 аксимально сильным подграфом графа G=(X,A) является сильный подграф, который не содержится в любом другом сильном подграфе графа G. Такой подграф называется сильной компонентой графа G.

Пример 9.

Порождённый подграф < {x₁, x₄, x₅, x₆} >

является сильной компонентой графа G.

В орграфе существует одна и только одна сильная компонента (СК), содержащая данную вершину x_i. В самом деле, если вершина x_i принадлежала бы двум или большему числу сильных компонент графа, то существовал бы путь из любой вершины одной СК в произвольную вершину другой СК, и объединение этих сильных компонент было бы сильно связанным графом, а это противоречит определению СК.

Если вершина x_i одновременно является начальной и конечной вершиной пути, то множество вершин, существенных относительно концов пути x_i x_i, определяются как пересечение R(x_i)  Q(x_i). Поскольку все эти существенные вершины достижимы из x_i и из каждой такой вершины достижима x_i, то все они взаимно достижимы. Следовательно, множество R(x_i)  Q(x_i), которое может быть построено с помощью формул (1) и (2), однозначно определяет сильную компоненту графа G, содержащую вершину x_i.

§ 2.9.3. Конденсация графа. Базы.

Если вершины найденной сильной компоненты удалить из графа G = (X,Г), то в оставшемся порождённом графе G = <X - R(x_i)  Q(x_i)> можно выделить новую СК, содержащую x_j  X - R(x_i)  Q(x_i). Эту процедуру можно повторять до тех пор, пока все вершины графа G не будут сгруппированы в соответствующие сильные компоненты.

Опр 5. Пусть В – некоторое подмножество вершин графа G. Обозначим через R(B) множество вершин, достижимых из вершин множества В, т.е. R(B)=R(x_i) по всем элементам множества В.

В является базой тогда и только тогда, когда R(B)=Х и  SB R(S)X.

Т.е. из множества В достижимы все вершины графа, и не существует строгого подмножества В, обладающего этим свойством. Отсюда следуют два утверждения:

1. в множестве вершин В нет двух вершин, которые принадлежат одной и той же СК графа G.

2. в любом графе без циклов существует единственная база; она состоит из всех таких вершин, полустепени захода которых равны нулю.

Следовательно, базы графа можно строить так: из каждой сильной компоненты графа надо взять по одной вершине.

§ 2.10. Пути между заданными вершинами

§ 2.10.1. Кратчайший путь между двумя заданными вершинами s и t

Пусть дан граф G=(X,A), дугам которого приписаны веса (стоимости), задаваемые матрицей весов С=[c_ij]. Задача о кратчайшем пути состоит в нахождении кратчайшего пути от заданной начальной вершины sX до заданной конечной вершины tX, при условии, что такой путь существует, т.е. при условии tR(s). Здесь R(s) – множество вершин, достижимых из вершины s. Элементы матрицы весов С могут быть положительными, отрицательными или нулями. Единственное ограничение состоит в том, чтобы граф G не содержал циклов с суммарным отрицательным весом. Если такой цикл Ф существует, и x_i – некоторая его вершина, то двигаясь от s к x_i , обходя затем Ф достаточно большое число раз и попадая, наконец, в t, мы получим путь со сколь угодно малым (в пределе стремящимся к бесконечности) весом. Поэтому будем считать, что все циклы графа G имеют неотрицательный суммарный вес.

Непосредственным обобщением данной задачи о кратчайшем пути являются следующие задачи:

1. Для данной начальной вершины s найти кратчайшие пути между s и всеми другими вершинами x_i  X.

2. Найти кратчайшие пути между всеми парами вершин.