ТГ

Тема 2. Элементы теории графов.

Леонард Эйлер (1707 – 1783)

Родился в Швейцарии, г. Базель. Отец был пастором. В Базельском университете Л.Э. готовился к карьере священника по желанию отца, но также посещал математические лекции профессора Иоганна Бернулли, который принадлежал научной школе Лейбница.

В 1725 году в России организовывалась Петербургская академия наук, Л.Э получил приглашение преподавать здесь. Он согласился, но приехал в Россию только через два года, в 1727 году, закончив университет. Вскоре мировая математическая общественность единодушно признала его первым математиком мира. В 1741 году, когда Россией правила Анна Леопольдовна, и науки не входили в круг её интересов, Л.Э уезжает в Берлинскую академию наук. В 1966 г. он вновь возвращается в Россию.

В последние годы жизни он почти совсем потерял зрение, писать сам не мог, поэтому диктовал ученикам. Только за один 1777 год он с секретарём подготовил 100 статей – почти 2 статьи в неделю.

Умер Эйлер в 1783 году в возрасте 76 лет. Он оставил более 800 научных трудов, причём многие из них – 2-3 томные издания. Его статьи издавались в академическом журнале, и после его смерти продолжали издаваться в течение 80 лет!

Эйлер был самым разносторонним математиком, занимался всеми вопросами современной ему математики и её приложениями, а некоторые разделы стал разрабатывать впервые. Его интересовали:

• теория чисел;

• теория движения луны;

• геометрия;

• оптические приборы;

• алгебра;

• сопротивление материалов;

• тригонометрия;

• баллистика;

• первая теория расчёта действия турбин;

• основы теории гироскопа;

• начала топологии и мн. др.

Н ачало теории графов все единодушно относят к 1736 году, когда Л. Эйлер не только решил популярную в то время задачу о Кёнигсбергских мостах, но и нашёл критерий существования в графе специального маршрута (Эйлерова цикла).

Задача о мостах. Река образует острова. Через два речных рукава перекинуто 7 мостов.

Спрашивается, можно ли пройти все 7 мостов так, чтобы каждый был пройден по одному лишь разу.

Через век, в середине 19 столетия, теория графов была продвинута инженером – электриком Кирхгофом, который разработал теорию деревьев для исследования электрических цепей.

Нигде в других науках теория графов долго не применялась и развивалась только в приложениях: игры, занимательные задачи, математические ребусы.

Термин «граф» впервые появился в книге выдающегося венгерского математика Кёнига в 1936 году. За последние ¾ столетия теория графов превратилась в один из наиболее развитых разделов математики. Одна из причин - становление и развитие науки об управлении кибернетики. Теория графов является существенной частью математического аппарата кибернетики.

§ 2.1. Основные понятия.

Опр.1. Пусть V – непустое множество, Е¹² – множество всех его двухэлементных подмножеств, Е– любое подмножество множества Е¹² (Е  Е¹²). Тогда пара G = (V,E) называется графом (неориентированным графом). Элементы множества V называются вершинами, а множества Е – ребрами графа.

Вершины и рёбра графа называются элементами графа. Число вершин графа G (мощность множества вершин V) называется порядком графа и обозначается │G│. Если │G│=n, а число его рёбер │Е│=m, то G называют (n,m)-графом.

Приведённое определение графа является весьма абстрактным. Для наглядности представления введём геометрическую интерпретацию графа. С этой целью будем рассматривать в евклидовом пространстве фигуры определённого вида. Каждая из этих фигур g состоит из различных вершин b₁, b₂, b₃ … и кривых (дуг или отрезков прямых), каждая из которых соединяет некоторую пару вершин b_i, b_j. Возможно вырождение b_i = b_j. Предполагается, что никакая внутренняя точка кривой не является вершиной или внутренней точкой другой кривой.

Опр.2. Фигура g называется геометрической интерпретацией графа G, если существует взаимно однозначное соответствие между вершинами фигуры g и вершинами графа G, а также между кривыми фигуры g и рёбрами графа G, такое, что соответствующие кривые и рёбра соединяют соответствующие вершины.

Спрашивается, любой ли граф можно реализовать в евклидовом пространстве и какова мерность пространства для реализации любого графа? В теории графов существует теорема, в которой доказывается, что каждый конечный граф G можно реализовать в трёхмерном евклидовом пространстве.

Пример 1.

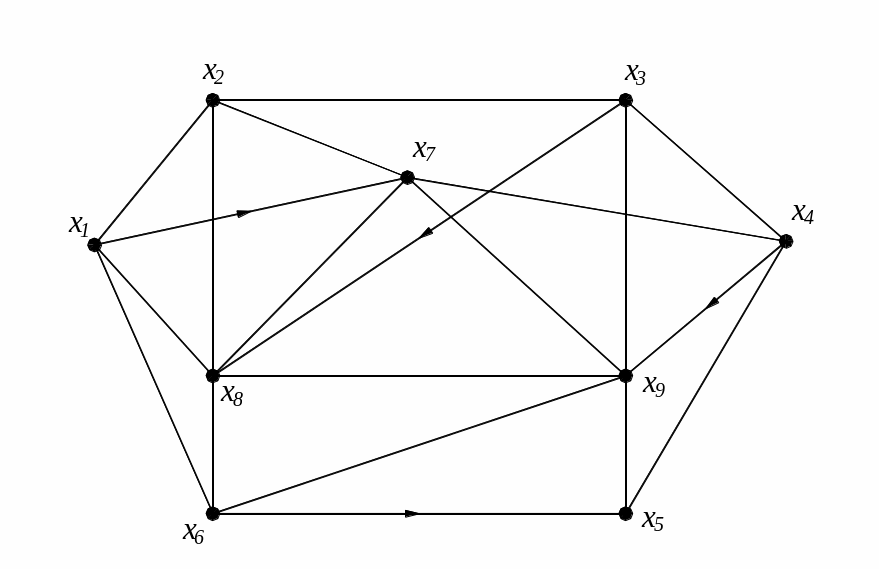
Пусть дан граф G = (V,E). Ребро {u, v}E обозначают uv. Говорят, что ребро uv соединяет вершины u и v, а вершины u и v являются концевыми для данного ребра.

Если порядок концевых точек ребра е безразличен, то говорят, что е – неориентированное ребро. Как уже говорилось, обозначается ребро е = {а,b}. Если этот порядок важен, то е называют ориентированным ребром – дугой. Обозначается в этом случае ориентированное ребро (дуга) е = (a,b), причём (a,b)(b,а). При этом а называют начальной вершиной дуги, а b – конечной вершиной. На рисунках дуги обозначают стрелками.

Граф, состоящий из неориентированных рёбер, называется неориентированным графом. Граф, состоящий из ориентированных рёбер, называется ориентированным графом, орграфом. Элементы множества Х графа G называются вершинами, как и в случае неориентированного графа, а элементы множества А – дугами орграфа. При геометрической интерпретации дуги графа обозначаются линиями со стрелками, направленными от первого элемента дуги ко второму. При этом первый концевой элемент дуги называется её началом, а второй (на который указывает стрелка) – её концом. Петлёй называется дуга, начальные и конечные вершины которой совпадают.

Чтобы от неориентированного графа перейти к ориентированному, надо удвоить каждое его ребро и придать каждой получившейся паре рёбер противоположную направленность.

Чтобы перейти от ориентированного графа к неориентированному (получить его неориентированный двойник), надо пренебречь направлением дуг орграфа. Обозначается операция пренебрежения направлением дуг следующим образом: .