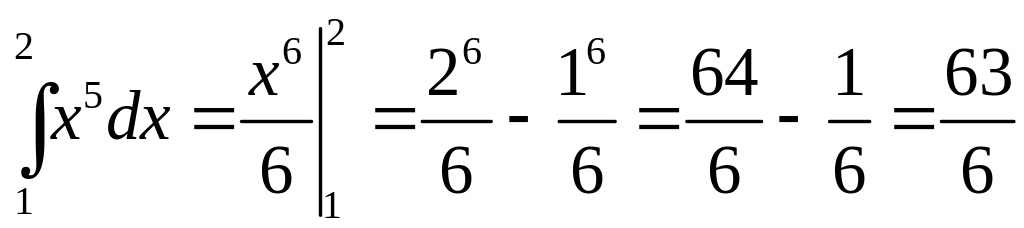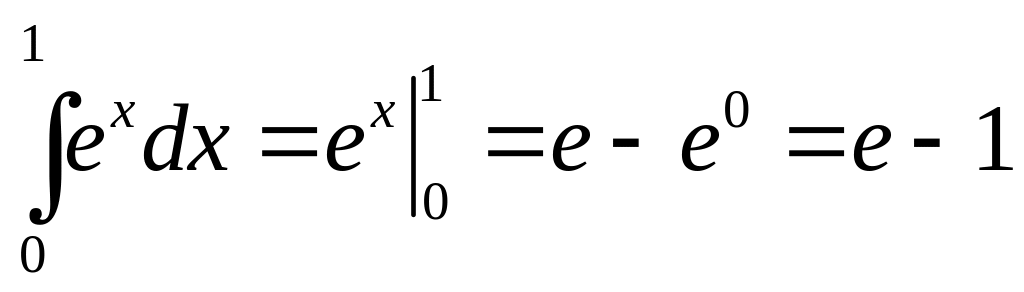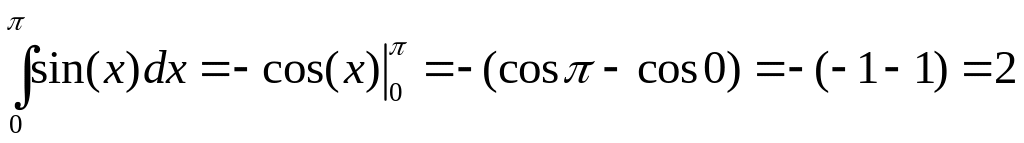11. Определённый интеграл.
Пусть на отрезке
[a,b]
задана непрерывная функция
.
Разобьем отрезок [a,b]
произвольным образом на n
частей точками
где
.
Обозначим
внутри отрезка выберем произвольно
точку
и
вычислим значения функции
Сумма произведений
вида
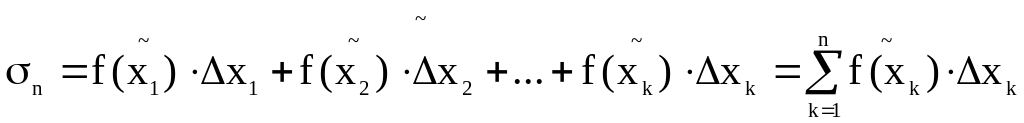
Называется
интегральной
суммой для
функции f(x)
на отрезке [a,b].
Т. к. функция f(x)
– непрерывна, то
где
соответственно
наименьшее и наибольшее значения функции
f(x)
на отрезке [xk-1,
xk].
Умножая все члены последнего неравенства
на
получим
Если
на отрезке [a,b],
геометрический смысл последнего
неравенства мы разбирали.
Предел
и
существует и не
зависит от способа разбиения отрезка
[a,b]
на части, причём
.
На основании
свойства пределов существует
.
Определение: если
при любых разбиениях отрезка [a,b],
и при любом выборе точек
на
отрезках [xk-1,
xk]
интегральная сумма
стремится к одному и тому же пределу S,
то этот предел называют определённым
интегралом
от функции f(x)
на отрезке [a,b]
и обозначают
.
Т
Число a называют нижним пределом,
b- верхним пределом. Отрезок [a,b] называют отрезком интегрирования, Х-переменной интегрирования.
Если
на отрезке [a,b],
то
численно равен площади
криволинейной трапеции,
ограниченной кривой y=f(x),
прямыми x=a,
x=b
и осью ОХ
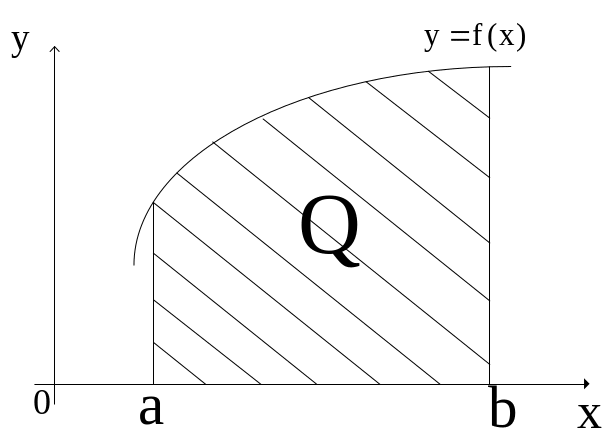
Замечание1: Определённый интеграл зависит только от вида ф-ии f(x) и пределов интегрирования, но не зависит от переменной интегрирования, которую можно обозначить любой буквой.
.
Замечание2:
из определения определённого интеграла
следует, что
.
Замечание3:
при a=b,
.
Пар.12. Основные свойства определённого интеграла.
1) постоянный
множитель можно выносить за знак
определённого интеграла
,
где А-const.
2) определённый интеграл от алгебраической суммы нескольких функций равен алгебраической сумме от интегралов слагаемых.
3) если на отрезке
[a,b],
где а<b,
функции f(x)
и
удовлетворяют условию f(x)
,
то
.
4) если m
и M
– наименьшее и наибольшее значения
функции f(x)
на отрезке [a,b]
и
то
5) теорема о среднем.
Если функция f(x)
непрерывна на отрезке [a,b],
то на этом отрезке найдётся такая точка
что
справедливо следующее равенство
6) для любых трёх
чисел a,
b,
c
справедливо равенство,
если только эти три интеграла существуют.
Доказать все эти свойства самостоятельно.
§13 Вычисление определённого интеграла. Формула Ньютона-Лейбница.
Пусть в определённом
интеграле
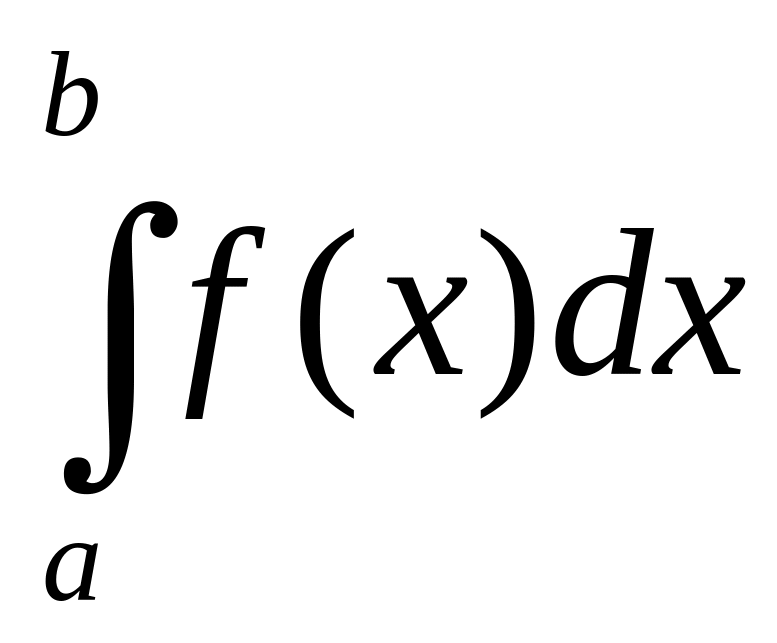нижний предел а закреплён, а верхний
предел b меняется.
Тогда будет меняться и значение интеграла,
т.е. интеграл есть ф-ия верхнего предела.
Перейдём к привычным обозначениям: верхний предел обозначим через x, а переменную интегрирования через t.
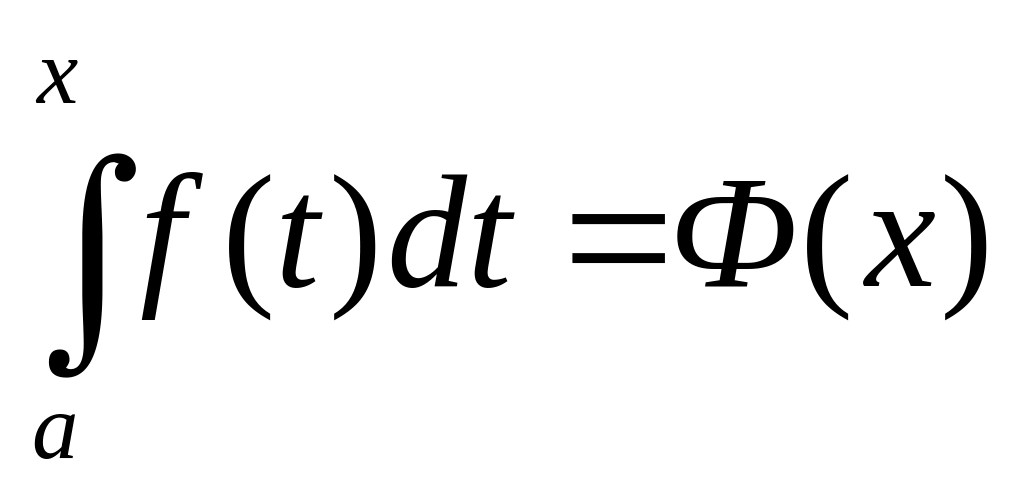, где
a – const.
Если f(t)≥0, то Ф(х) – численно равна площади криволинейной трапеции аАХх (Рисунок 1).
Рисунок 1 – График функции f(x).
Теорема 1.
Если ф-ия f(x)
– непрерывная функция и
,
то имеет место равенство Ф‘(х) = f(x).
Или: производная от определённого интеграла по верхнему пределу равна подынтегральной ф-ии, в которую вместо переменной интегрирования подставлено значение верхнего предела.
Док-во. По определению производной имеем:
;
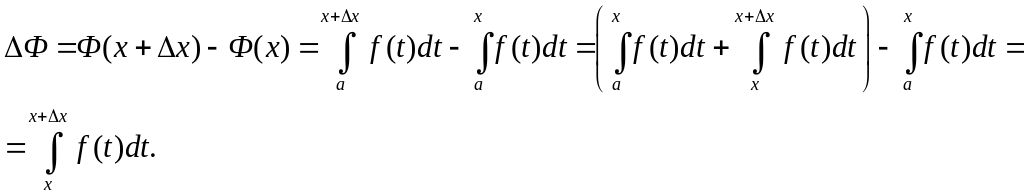
По теореме о среднем:
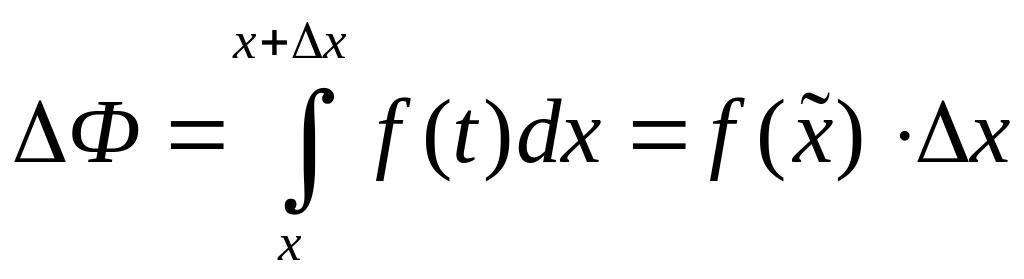, где
Найдём
.
След-но
,
т.к.
при
.
Теорема доказана.
Замечание. Из доказанной теоремы следует, что если ф-ия f(t) – непрерывна на отрезке [a, x], то сущ-ет ф-ия и она является первообразной для ф-ии f(x), то справедлива формула:
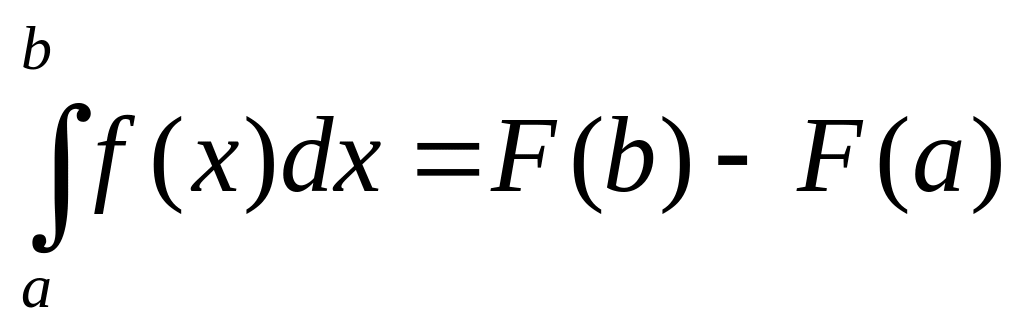(1)
Эта формула наз. формулой Ньютона-Лейбница.
Док-во.
Пусть F(x)
– есть некоторая первообразная от ф-ии
f(x).
По теореме 1
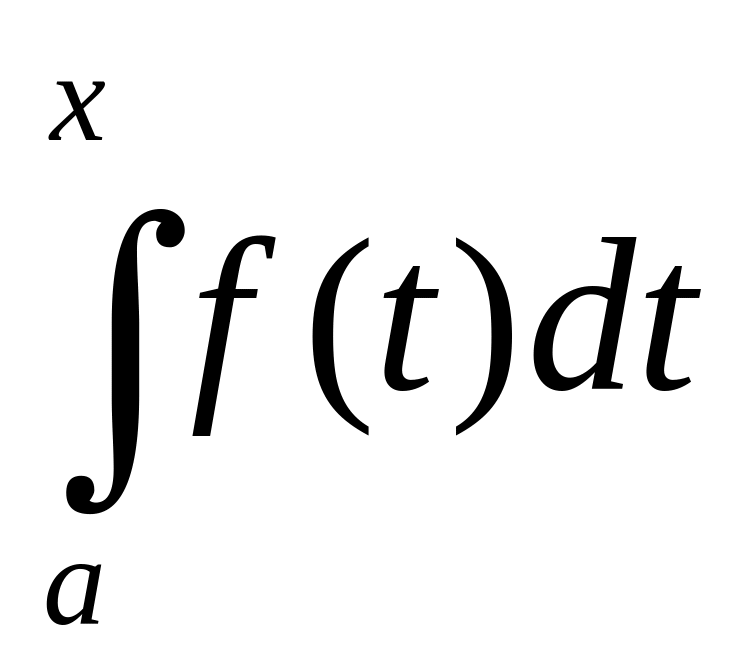есть такая же первообразная от ф-ии
f(x),
а две первообразные от данной ф-ии
отличаются на постоянное слагаемое С*:
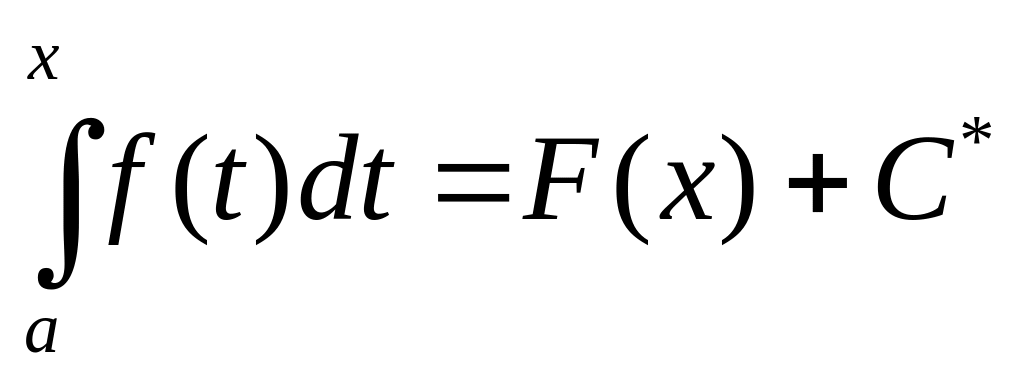. (2)
Это равенство при соответствующем значении С* верно для всех х, т.е. являются тожд-ом.
При х = а имеем:
;
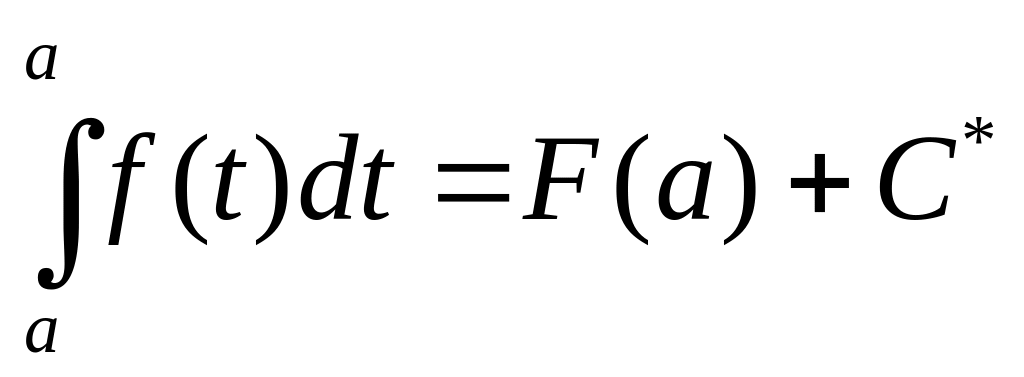0 = F(a)+C*, откуда С* = - F(a).
При х = b равенство (2) будет:
.
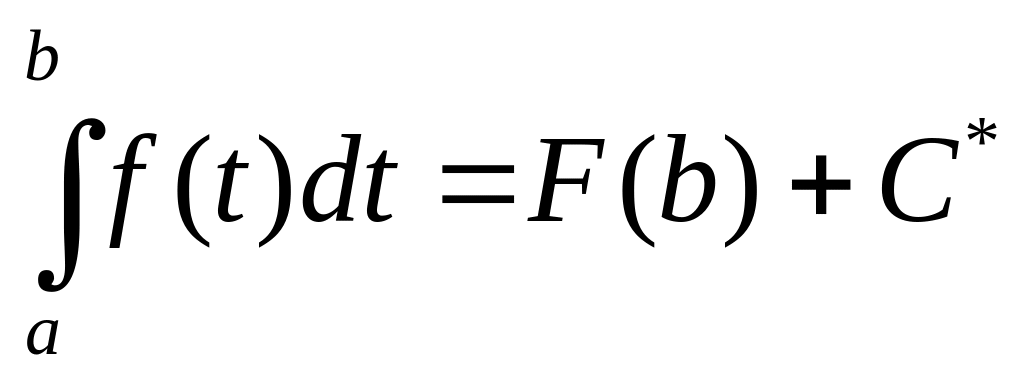Заменив переменную t на х получим ф-лу Ньютона-Лейбница:
.
Её можно, при решении, записать так:
.
Примеры:
