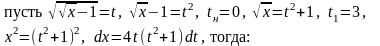I. Понятие определенного интеграла
Пусть на [a;b] задана непрерывная функция у =f(x).
Разобьем
отрезок [a;
b]
на n
частичных отрезков с помощью
произвольно выбранных на нем точек
.
На каждом из отрезков (частичных) возьмем произвольные точки ξi (i=1,2,3…n). Во взятых точках вычислим значения функции f(x): f(ξ1), f(ξ2), f(ξ3)…, f(ξn).
Составим произведения длин ∆x1 , ∆x2, …,∆xn частичных отрезков на значения функции f(ξi).
Все эти произведения сложим и выразим сумму их через
(1)
где σ=f(ξ1)∆х1+f(ξ2) ∆х2+f(ξ3)∆х3+…+ f(ξn)∆хn; или
Сумму такого вида называют интегральной суммой, составленной для функции f(x) на отрезке [a;b].
Будем неограниченно увеличивать число делений отрезка [a;b] однако так, чтобы длина ∆xi каждого отрезка [xi-1;x] стремилась к нулю; и рассмотрим получающееся при этом множество интегральных сумм σ.
Если при этом разбиении интегральные суммы будут стремиться к одному и тому же пределу, то этот предел называют определенным интегралом от функции f(x) на отрезке[a;b].
Определение.
Если
существует предел
суммы
(1) при ∆хi→0,
то
говорят, что функция f(x)
интегрируема на [a;b],
число
I
называют определенным интегралом от
функции f(x)
на [a;b].
,
где числа «а» и «b» называются пределами интегрирования (или интеграла), соответственно нижним, верхним; отрезок [a;b] – промежутком интегрирования.
1. 1. Основные свойства определённого интеграла
1. По определению
.
2. По определению .
3. Каковы бы ни были числа a, b, c, всегда имеет место равенство
.
4. Постоянный множитель можно выносить за знак определённого интеграла, т. е.
.
5. Определённый интеграл от алгебраической суммы функции равен алгебраической сумме их интегралов, т. е.
.
1. 2. Формула Ньютона-Лейбница
Если функция f(x) непрерывна на отрезке [a;b] и F(x) есть какая-либо первообразная для f(x) на этом отрезке, то справедлива следующая формула:
=F(b)-F(a) . (2)
Пример 1. Вычислить:
.
Решение: применим формулу Ньютона-Лейбница:
=F(x)|
=F(b)
- F(a)
Преобразуем подынтегральную функцию
.
1.3. Интегрирование по частям в определенном интеграле
Пусть функции U(x) и V(x) имеют непрерывные производные на [a;b], тогда справедлива формула
. (3)
Пример 2. Вычислить:
.
Решение: пусть
,
т. к. функции
и
непрерывны на
вместе со своими производными, то
согласно формуле (I) находим
.
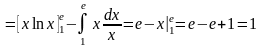1.4. Замена переменной в определенном интеграле
Пусть
требуется вычислить
,
где
f(x)
-
непрерывная на [a;b]
функция. Часто
здесь бывает удобно применить, как и в
случае вычисления неопределенного
интеграла, замену переменной путем
введения вместо
старой переменной новой переменной t,
связанной
со старой
соотношением
.
Итак, введем новую переменную t , положив .
Пусть выполняются следующие условия:
а) функция
определена
и непрерывна на отрезке
;
б) при
изменении t
на
значения функции
не выходят
за пределы отрезка
.
При этом
;
в) Функция
на отрезке
имеет непрерывную производную
.
Тогда имеет место равенство
(4)
При пользовании формулой (4) следует функцию стараться выбирать так, чтобы новый интеграл был более простым для вычисления, чем первоначальный.
Пример
3. Вычислить:
Решение: применим
подстановку:
.
Найдем пределы
интегралов для новой переменной при
,
при
.
Следовательно, при применении x от 1/3 до 1 новая переменная t изменяется от 3 до 1.
Функция
-
убывает
и непрерывна вместе
со своей производной
на отрезке
Пример
4. Вычислить:
.
Решение.
