
- •Часть 2
- •Часть 2
- •Оглавление
- •4.1. Основные сведения 12
- •5.1. Основные сведения 22
- •Введение
- •Лабораторная работа 3
- •На устойчивость систем
- •3.1. Основные сведения
- •3.2. Порядок выполнения работы
- •3.3. Контрольные вопросы
- •Лабораторная работа 4 точность систем и методы ее повышения
- •4.1. Основные сведения
- •4.2. Порядок выполнения работы
- •4.3. Контрольные вопросы
- •Лабораторная работа 5 качество процессов управления и методы его обеспечения
- •5.1. Основные сведения
- •5.2. Порядок выполнения работы
- •5.3. Контрольные вопросы
- •Библиографический список
- •Часть 2
- •644046, Г. Омск, пр. Маркса, 35
Лабораторная работа 3
УСТОЙЧИВОСТЬ СИСТЕМ. ВЛИЯНИЕ ПАРАМЕТРОВ
На устойчивость систем
Цель работы: знакомство с понятием и основной теоремой устойчивости линейных систем, с методом Д-разбиения, оценивающим влияние параметров на устойчивость и экспериментальное определение границ Д-разбиения.
3.1. Основные сведения
Под устойчивостью, или (более корректно) под устойчивостью процессов управления, понимается работоспособность, т. е. способность системы в принципе отрабатывать входные воздействия. Для исследования свойств устойчивости вводится в рассмотрение ошибка
![]() , (3.1)
, (3.1)
где x(t)
– входное (задающее) воздействие; y(t)
– выходная переменная.![]()
Требованием соблюдения устойчивости является выполнение в переходном режиме условия:
![]() . (3.2)
. (3.2)
Линейная система в разомкнутом состоянии описывается передаточной функцией:
 , (3.3)
, (3.3)
где R(s)
и Q(s)
– полиномы степеней m и
n соответственно (n
![]() m).
m).
Устойчивость оценивается для замкнутых систем и для них справедливо выражение
![]() (3.4)
(3.4)
или в полиномиальной форме –
 . (3.5)
. (3.5)
В формуле (3.5) выражение D(s) называют характеристическим полиномом замкнутой системы, который, как и Q(s), имеет степень, равную n и записывается в виде:
![]() . (3.6)
. (3.6)
В развернутой форме
![]() , (3.7)
, (3.7)
где
![]() – коэффициенты характеристического
полинома.
– коэффициенты характеристического
полинома.
(Напомним,
что
![]() являются также и параметрами левой
части дифференциального уравнения,
описывающего процессы в замкнутой
системе.)
являются также и параметрами левой
части дифференциального уравнения,
описывающего процессы в замкнутой
системе.)
Характеристическое уравнение записывается в виде:
![]() (3.8)
(3.8)
или
![]() . (3.9)
. (3.9)
В теории управления доказана основная теорема устойчивости, в соответствии с которой для устойчивости линейной системы необходимо и достаточно, чтобы корни характеристического уравнения (3.9) имели бы отрицательные вещественные части [3, 4].
Аналитически условия теоремы соответствуют выполнению неравенств:
![]() (3.10)
(3.10)
В выражении (3.10) корни si являются корнями уравнения (3.8), поэтому справедливо выполнение тождеств:
![]() (3.11)
(3.11)
Заметим, что si также называют полюсами передаточной функции Ф(s) замкнутой системы.
Существует и другая формулировка основной теоремы [3, 4]. Для этого вводится в рассмотрение комплексная плоскость корней. Система устойчива при условии, если все ее корни располагаются в левой полуплоскости. Попадание хотя бы одного корня в правую полуплоскость означает неустойчивость системы управления (расходящийся характер переходных процессов). Мнимая ось в общем случае является колебательной границей устойчивости и при нахождении на ней хотя бы одной пары мнимых корней в переходном режиме устанавливаются незатухающие колебания. Начало координат соответствует апериодической границе устойчивости.
Естественно, что если в уравнении (3.9) изменить численное значение хотя бы одного из коэффициентов ai, то корни si будут другими и возможно нарушение условия устойчивости (3.10). Наиболее распространенными методами анализа влияния параметров на расположение корней, а следовательно, и на устойчивость являются корневой годограф [3] и Д-разбиение [3, 4].
В методе Д-разбиения пространство параметров разделяется на подобласти с одинаковым числом корней в левой и правой полуплоскостях. Рассмотрим Д-метод на примере системы третьего порядка и проанализируем влияние двух параметров A и B на ее устойчивость.
Допустим, что характеристическое уравнение можно записать в виде:
![]() (3.12)
(3.12)
Изменим
параметры A и B
так, что один или два корня полинома
![]() будут
перемещаться из левой полуплоскости в
правую, поэтому при некоторой
будут
перемещаться из левой полуплоскости в
правую, поэтому при некоторой
![]() они обязательно попадут на мнимую ось,
т.е.
они обязательно попадут на мнимую ось,
т.е.
![]() .
.
Подставляя в выражение (3.12), получим для определения Д-границы или Д-кривой следующее уравнение:
![]() (3.13)
(3.13)
Левая часть выражения (3.13) представляет собой комплексную функцию, поэтому должны равняться нулю вещественная и мнимая части:
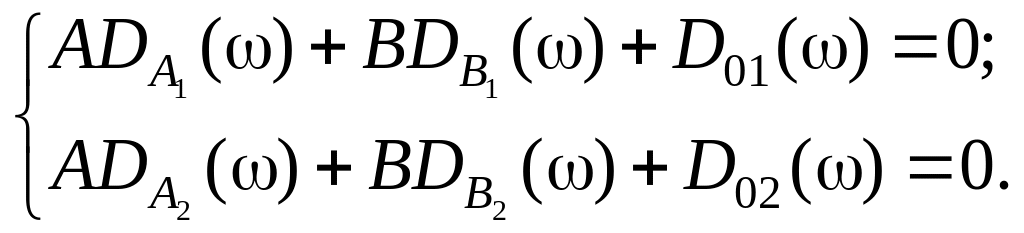 (3.14)
(3.14)
Система (3.14) получена из условия, что комплексные переменные представлены в виде:
![]() (3.15)
(3.15)
При
некоторой фиксированной частоте ω =
ω0 каждое из уравнений
системы (3.14) в плоскости параметров
представляет собой (описывает) прямую
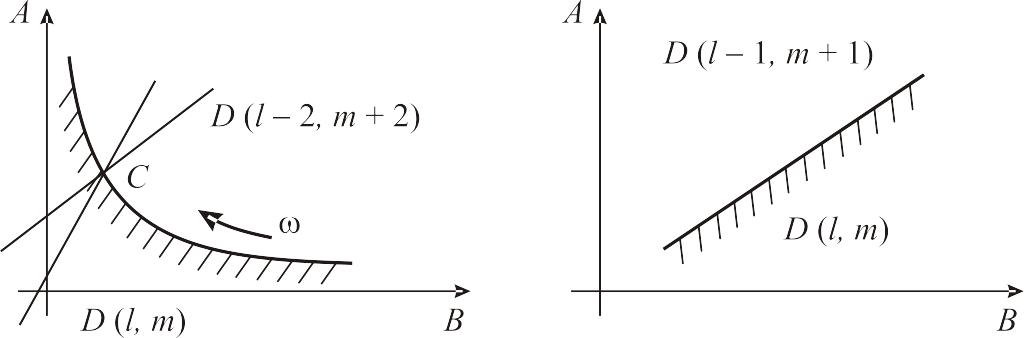
линию, как показано на рис. 3.1, а.
Решению должна удовлетворять точка
пересечения прямых С, которая и
является точкой Д-кривой при ω =
ω0. Для построения всей границы
необходимо изменить частоту от
![]() до
до
![]() .
.
 а
б
Рис. 3.1. Виды границ Д-разбиения
а
б
Рис. 3.1. Виды границ Д-разбиения
На Д-кривую наносят двойную штриховку, так как она соответствует переходу через мнимую ось двух корней. Если прямые на рис. 3.1, а совпадают (система не имеет решения), то они образуют особую прямую, вид которой приведен на рис. 3.1, б. Штриховка наносится одинарная, так как особая прямая соответствует апериодической границе устойчивости s = 0 и переходу только одного корня.
Полученные
области подписывают. Например, для
системы n-го порядка
обозначение
![]() означает,
что l корней находится
в левой, а m корней –
в правой, причем n = l + m.
означает,
что l корней находится
в левой, а m корней –
в правой, причем n = l + m.
Рассмотрим систему третьего порядка
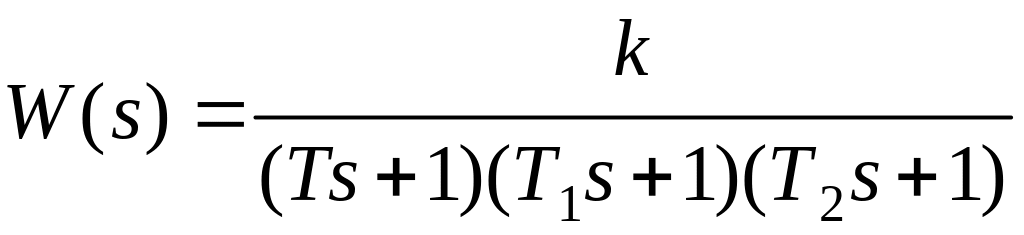 . (3.16)
. (3.16)
Передаточная функция замкнутой системы будет иметь вид:
 , (3.17)
, (3.17)
характеристическое уравнение –
![]() (3.18)
(3.18)
или в развернутой форме
![]() . (3.19)
. (3.19)
Допустим, что в качестве параметров А и В выбраны коэффициент передачи разомкнутой системы k и постоянная времени Т.
Уравнение (3.12) имеет вид:
![]() . (3.20)
. (3.20)
Заметим, что выражение (3.19) является частным случаем формулы (3.9), когда выполняется:
![]() ,
,
а для уравнений (3.20) и (3.12) справедливо:
![]() .
.
При
фиксированных Т1 и Т2,
используя рассмотренную методику, можно
построить кривую Д-разбиения, но
выражение (3.20) достаточно сложное,
поэтому приведем на рис. 3.2 качественный
вид Д-кривой. Особые прямые можно
получить из необходимых условий
устойчивости, т.е.
![]() и
и
![]() ,
поэтому они описываются уравнениями:
,
поэтому они описываются уравнениями:
![]() (3.21)
(3.21)
В
Рис. 3.2. Д-разбиение для системы
третьего порядка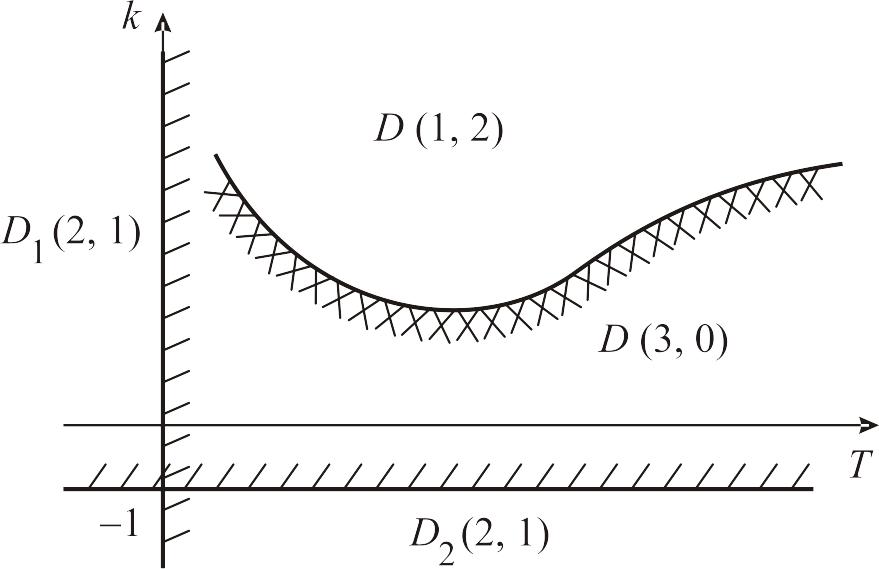
При
этом нахождению на Д-кривой
соответствует незатухающий переходный
процесс или запас устойчивости по фазе
![]() ,
если использовать логарифмические
характеристики.
,
если использовать логарифмические
характеристики.
