Предисловие

Данное методическое пособие предназначено для студентов специальности 160403 «Системы управления летательными аппаратами» по выполнению лабораторных работ по дисциплине «Системы аналитических вычислений». Цель данного пособия - закрепление теоретических материалов по численным методам интегрирования дифференциальных уравнений первого порядка, дифференциальных уравнений - го порядка и систем дифференциальных уравнений. В методическом пособии изложены одношаговые и многошаговые методы интегрирования дифференциальных уравнений. В лабораторных работах приведены варианты заданий – конкретные виды дифференциальных уравнений. Пособие может служить основой для выяснения усвоения студентами практических знаний по численным методам решения дифференциальных уравнений.

1. Основные численные методы решения дифференциальных уравнений

Целью данной главы учебного пособия является рассмотрение основных численных методов интегрирования дифференциальных уравнений [1,2,3].

Численные методы решения дифференциальных уравнений используются в тех случаях, когда не удается найти их решение в аналитическом виде. Прежде всего, это относится к линейным дифференциальным уравнениям с переменными коэффициентами и нелинейным дифференциальным уравнениям, соответственно описывающим динамику линейных нестационарных и нелинейных систем управления.

С помощью данных методов, прежде всего, решаются задачи исследования систем.

В данной части пособия ограничимся рассмотрением методов решения только для задачи Коши.

1.1. Метод Эйлера решения задачи Коши

Рассмотрим дифференциальное уравнение

. (1.1)

Предположим, что функция дифференцируема в некоторой окрестности точки . Задача Коши для дифференциального уравнения (1.1) формулируется следующим образом: найти решение уравнения (1.1), удовлетворяющее условию .

Предположим, что известно решение в точке и требуется найти , где – шаг интегрирования. Согласно формуле Ньютона – Лейбница, очевидным является следующее равенство

.

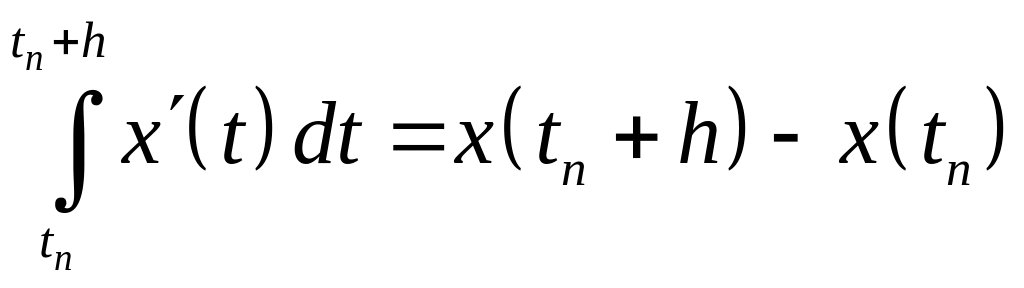Запишем его следующим образом

.

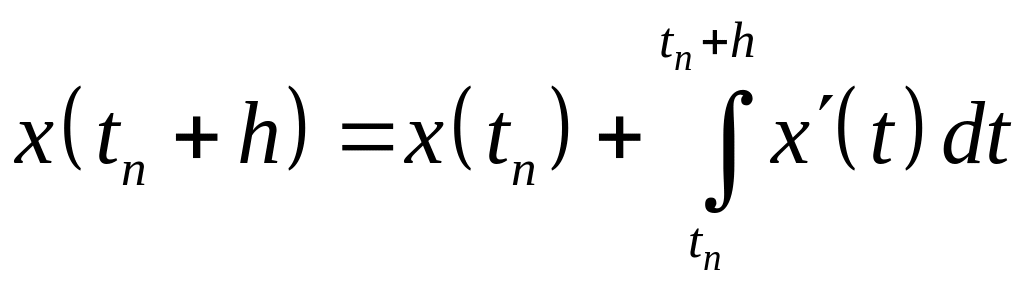Учитывая уравнение (1.1), последнее равенство можно записать в виде

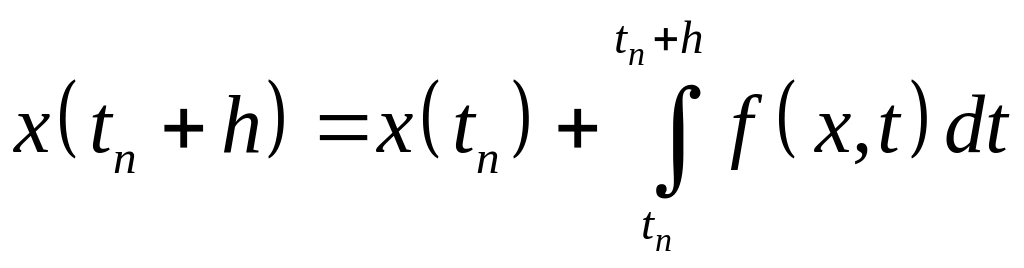. (1.2)

Интеграл в правой части выражения (1.2) приближенно можно вычислить, используя формулу прямоугольников:

.

Здесь . Отбрасывая члены порядка и полагая , , получаем известную формулу Эйлера

, . (1.3)

Аналогичный результат можно получить и другим способом. Для этого разложим функцию в ряд Тейлора в окрестности точки , в результате получим

(1.4)

или

.

В последнем выражении ограничимся двумя первыми слагаемыми в правой части. В результате получаем

, .

Полагаем, что решение в точке известно. Тогда решение в точке можно найти, используя последнюю формулу и учитывая, что :

(1. )

или

, .

Начинать вычислительный процесс необходимо с точки, определяющей начальные условия, то есть .

Вычислительный процесс, построенный по формуле (1.3), имеет локальную погрешность, пропорциональную . Это означает, что на каждом шаге интегрирования имеет место погрешность порядка . Соответственно, при увеличении времени интегрирования общая погрешность решения дифференциального уравнения возрастает.

Повысить точность получаемых результатов можно, если учитывать большее количество членов разложения функции в ряд Тейлора. Однако, для этого необходимо последовательно дифференцировать правую часть дифференциального уравнения (1.1).

Рассмотрим это на конкретном примере.

Учтем первые четыре члена в ряде Тейлора, в результате получим

.

Как и ранее, полагаем, что решение в точке найдено. Выбирая достаточно малый шаг , находим решение в следующей точке

.

Для реализации этой формулы необходимо знать производные искомого решения , , . Первая производная может быть найдена из дифференциального уравнения (1.1). Это есть его правая часть, . Вторую и третью производные решения – , – можно найти, дифференцируя правую часть уравнения (1.1), рассматривая ее, как сложную функцию. Соответственно имеем

,

, (1.5)

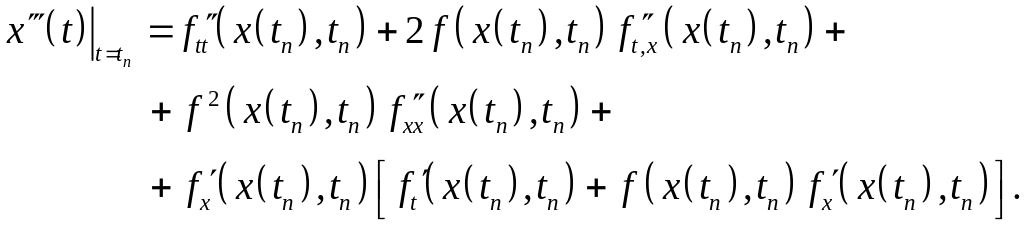
Как видим, такой путь повышения локальной точности решения дифференциального уравнения (1.1) является трудоемким.

Точность вычислений можно повысить при заданном шаге интегрирования и другими способами. В формуле (1.2) интеграл вычисляется по формуле прямоугольников. Вычислим этот интеграл, используя формулу трапеций. В результате будем иметь

.

По формуле Тейлора, справедливо равенство

.

Отбрасывая в последнем выражении члены порядка , и полагая

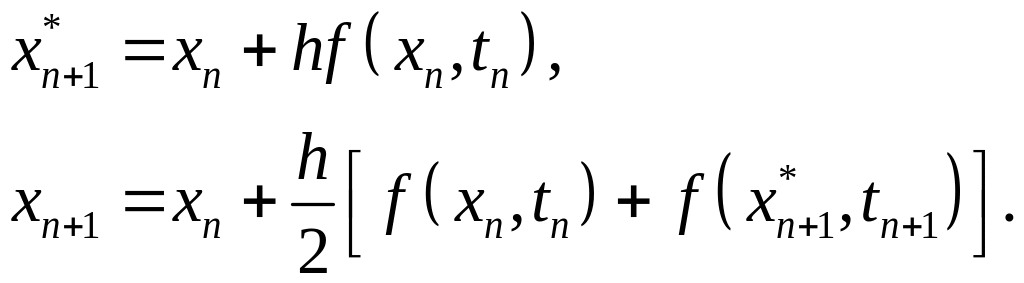(1.6)

Здесь .

Погрешность, которая обеспечивается этими формулами, имеет порядок . Формулы (1.6) называются формулами Эйлера – Коши.